ekstrema funkcji Rafał: oblicz ekstrema funkcji ln(1−x²)

konrad: https://matematykaszkolna.pl/strona/387.html

Rafał: dobrze tylko mam problem z policzeniem..

konrad: z policzeniem czego, pochodnej?

Basia: 1−x²>0 ⇔ x∊(−1;1)

	1		−2x
f'(x) =		*(−2x) =
	1−x2		1−x2

i w czym problem ?

Rafał: DO TEGO MIEJSCA WIEM A CO DALEJ?

Basia: szukasz miejsca zerowego pochodnej ułamek = 0 ⇔ jego licznik = 0 w przedziale (−1;1) mianownik jest stale dodatni ⇒ znak pochodnej zależy tylko od licznika

Rafał: nie rozumie..

Basia: co to znaczy znaleźć miejsce zerowe pochodnej ? to znaczy rozwiązać równanie f'(x) = 0

2x
	= 0 ⇔ 2x=0 ⇔ x=0
1−x2

teraz badasz znak pochodnej dla x∊(−1;1) 1−x²>0 czyli znak pochodnej zależy tylko od licznika 2x<0 ⇔ x<0 2x>0 ⇔ x>0 x∊(−1;0) ⇒ f'(x) <0 ⇒ f↘ x∊(0;1) ⇒ f'(x)>0 ⇒ f↗ to co funkcja osiąga dla x=0 ?

Rafał: zabij mnie ale dalej niewiem..

Basia: to może poczytaj jednak nieco teorii https://matematykaszkolna.pl/strona/387.html

Rafał: aha czyli w 0 osiąga max?

Rafał: odwrotnie w x=0 osiąga minimum

konrad: tak

Rafał: to max osiaga w 1 i −1 ?

konrad: znaczy nie, w x=0 jest max

konrad: jest tylko maksimum w punkcie x=0 Basia chyba się pomyliła albo ja coś źle odczytuję

Rafał: a min?

konrad: nie ma

Rafał: a mógł byś to napisać od początku tak jak trzeba bo ja się w tym nie mogę odnaleźć..

konrad: skoro wyszło jedno miejsce zerowe to jest albo minimum albo maksimum

Basia: minus "zeżarłam" przy przepisywaniu czyli jest odwrotnie czyli x_max = 0 minimum nie ma

Maslanek: Ale punkty przegięcia byśmy znaleźli?

Basia: a dlaczego mielibyśmy nie znaleźć ?

Rafał: ja nie wiem ale Basia to ma chyba profesora z tej matematyki bo wszystko wie

Maslanek: Tak pytam

	2x
f'(x)=
	x2−1

	2x2−2−4x2		x2+1
f''(x)=		= −2*		.
	(x2−1)2		(x2−1)2

Chyba nie znajdziemy

Basia: nie wszystko

Basia: nie ma punktów przegięcia, bo pokazałeś, że funkcja w całej swojej dziedzinie jest wklęsła

Rafał: no nie licząc takich rzeczy jak np co jadłem dziś na obiad

Maslanek: Dzisiaj jest wtorek, więc najprawdopodobniej jadłeś śmieciówkę

Rafał: a to ze funkcja jest wklęsła mówi mi to ze jest −2x ?

Rafał: nie tak dobrze nie było na kebabie dzis jade w sumie 3

Maslanek: Raczej to, że druga pochodna jest zawsze ujemna

Rafał: ale mi chodzi o to ze jest minimum a nie maximum..

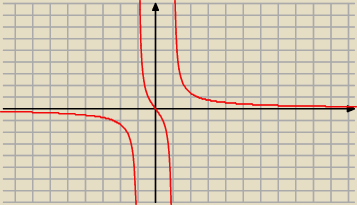
Maslanek: Z lewej rosnąca, z prawej malejąca. Czyli maksimum. Wykres to f'(x).

Basia: toż to jest f(x)= ln(1−x²); dziedzina = (−1;1) to i pochodna istnieje tylko w tej dziedzinie czyli tylko środkowa część wykresu

Maslanek: Tam i tak nie zwracałem uwagi, bo nie ma miejsca zerowego

Basia:

	−2x
ale tak czy owak to co narysowałeś jest wykresem funkcji g(x) =		,
	(1−x2)2

ale nie jest wykresem pochodnej funkcji f(x)=ln(1−x²)

Maslanek: Bez kwadratu na dole

Basia: a bez

Maslanek: Idę spać