proszę o pomoc w rozwiązaniu f.kwadratowej w postaci kanonicznej,iloczynon,monot wojtek: y= −1/2x² +6x−10

Piotr: https://matematykaszkolna.pl/strona/69.html

Buuu:

	−b		−Δ		−b ± √Δ
p =		; q =		; Δ = b2 − 4ac; x1 lub 2 =
	2a		4a		2a

kanoniczna y = a(x−p)² + q Iloczynowa y = a(x−x₁)(x−x₂) monotoniczność f↗ ⇔ x∊ (−∞, p); f↘ ⇔ x∊ (p, ∞)

C:

	1
y = −		x2 + 6x −10
	2

Δ = b² − 4ac = 36 − 20 = 16 √Δ = 4

	−b + √Δ		−b − √Δ
x1 =		= 2 x2 =		= 10
	2a		2a

	1
iloczynowa: y = a(x − x1)(x − x2) = −		(x − 2)(x − 10)
	2

−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−

	b		−6
p = −		=		= 6
	2a		−1

	−Δ		−16
q =		=		= 8
	4a		−2

	1
kanoniczna: y = a(x − p)2 + q = −		(x − 6)2 + 8
	2

magda: a mogę prosić o rozwiązanie tego zadania? byłbym wdzięczny

wojtek: dziękuję C za pomoc

magda: a na zbiór wartości i postać monotoniczną jest szansa ?

Mila:

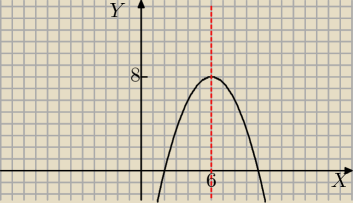
	1
1) parabola skierowana w dół, bo a=−		<0
	2

największa wartość w wierzchołku i wynosi 8 dla x=6 Z_w=(−∞,8) 2) naszkicuj wykres odczytaj dla jakich argumentów f. rośnie a dla jakich maleje.

magda: dziękujemy