funkcja kwadratowa Damian24: Oblicz największą wartość funkcji: f(x)=−2x²+10x−1 i wyznacz argument, w którym ta wartość jest przyjmowana.

Eta: https://matematykaszkolna.pl/strona/1683.html

Piotr: oblicz wspolrzedne wierzcholka

Sokoov: zauważ, że przy x² jest minus, więc parabola będzie miała ramiona w dół. Największą wartością funkcji będzie więc jej wierzchołek.

Damian24: a argumentem będzie... ?

Sokoov: no argument to współrzędna X

krystek: x_w argument y_w wartość największa

Gustlik: Czyli współrzedne wierzchołka paraboli:

	b
p=−		− argument
	2a

	Δ
q=−		lub q=f(p) − wartość dla tego argumentu.
	4a

Piotr: wypowiem sie. przeciez napisalem to na poczatku. wystarczy obliczyc wspolrzedne wierzcholka... i to jest to, ze nie wiedza co to argument, co to wartosc funkcji. a gbyby a>0 to nie daloby sie obliczyc najwiekszej wartosci (bez ograniczen ). i to tyle.

Mila:

	−10
xw=		=2,5
	−4

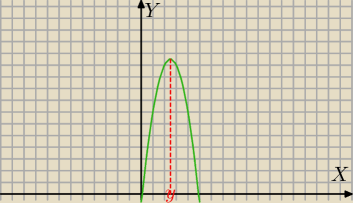
y_w=−2*(2,5)²+10*2,5−1 oblicz, to jest wartość największa