zadanie
;]: Na okręgu o środku O i promieniu r wybrano punkty A i B tak, Ŝe AB = 2r . Oblicz miarę
mniejszego kąta środkowego AOB.
Prosze o pomoc.
6 maj 16:55
df:
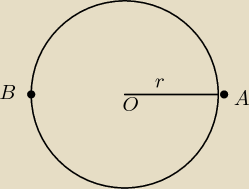
jak na mój gust nie ma innej możliwości, aby |AB|=2r jak tylko w przypadku gdy |AB| jest
średnicą... i tutaj są dwa kąty środkowe tej samej miary 180
0. ale może źle zrozumiałam
treść.
6 maj 17:05
;]: przepraszam zle napislam tam powinno być, że AB=
√2r

6 maj 17:12
:)))): dlatego prosze jeszcze o wsparcie

6 maj 17:15
tim: Ja pomogę.
6 maj 17:19
♊:
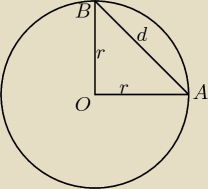
Trójkąt równoramienny o podstawie r
√2 i bokach r.
To jest jeden z bardziej charakterystycznych trójkątów ;
)
6 maj 17:21
♊: Wybacz tim − nie napisałem, ze pomagam ;P
6 maj 17:22
tim:
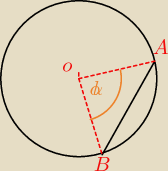
|AB| =
√2r
|AO| = |OB| = r
METODA A.
Korzystamy z tw. cosinusów.
|AB|
2 = |AO|
2 + |OB|
2 − 2|AO||OB|*sinα
2r
2 = 2r
2 − 2r
2*cosα
Wynika z tego, że cosα = 0, więc α = 90
O.
METODA B.
Jak wiemy
2280, jeżeli trojkąt ma boki a, a, a
√2 to jest prostokątny i ma kąty 45,45,90

6 maj 17:23
tim: No problemo. Ja znikam

6 maj 17:25
;))): dziękuję bardzo

6 maj 17:33
 jak na mój gust nie ma innej możliwości, aby |AB|=2r jak tylko w przypadku gdy |AB| jest
średnicą... i tutaj są dwa kąty środkowe tej samej miary 1800. ale może źle zrozumiałam
treść.
jak na mój gust nie ma innej możliwości, aby |AB|=2r jak tylko w przypadku gdy |AB| jest
średnicą... i tutaj są dwa kąty środkowe tej samej miary 1800. ale może źle zrozumiałam
treść.


 Trójkąt równoramienny o podstawie r √2 i bokach r.
To jest jeden z bardziej charakterystycznych trójkątów ;)
Trójkąt równoramienny o podstawie r √2 i bokach r.
To jest jeden z bardziej charakterystycznych trójkątów ;)
 |AB| = √2r
|AO| = |OB| = r
METODA A.
Korzystamy z tw. cosinusów.
|AB|2 = |AO|2 + |OB|2 − 2|AO||OB|*sinα
2r2 = 2r2 − 2r2*cosα
Wynika z tego, że cosα = 0, więc α = 90O.
METODA B.
Jak wiemy 2280, jeżeli trojkąt ma boki a, a, a√2 to jest prostokątny i ma kąty 45,45,90
|AB| = √2r
|AO| = |OB| = r
METODA A.
Korzystamy z tw. cosinusów.
|AB|2 = |AO|2 + |OB|2 − 2|AO||OB|*sinα
2r2 = 2r2 − 2r2*cosα
Wynika z tego, że cosα = 0, więc α = 90O.
METODA B.
Jak wiemy 2280, jeżeli trojkąt ma boki a, a, a√2 to jest prostokątny i ma kąty 45,45,90


