POmoc Bingos: GEOMETRIA ANALITYCZNA. Napisz równanie stycznej do okręgu przechodzącej przez punkt A. a) x² + y² = 8 , A = (4,0) b) x² + y² = 20 , A =(0,5)

Bizon: a) środek okręgu S=(0, 0) ... r=2√2 Styczna przechodząca przez A y−0=a(x−4) y=ax−4a Odległość środka okręgu od tej prostej to 2√2 ...wyznaczysz wsp. a

Nienor: A) Sposób I prosta: 0=4a+b b=−4a y=ax−4a i x²+y²=8, czyli x²+(ax−4a)²=8 → rozwiązujesz równanie z parmatrem x²+(ax−4a)²=8 x²+a²x²−8a²x+16a²=8 (1+a²)x²−8a²x+16a²−8=0 Δ=0 ⇔ (2−8a²)² − 4(1+a²)(16a²−8)=0

	6		−6
a=		lub a=
	8		8

Wkładamy a do wzoru prostej i otrzymujemy:

	3		−3
y=		x−3 lub y=		x+3
	4		4

Nienor: II sposób podał Bizon

Bingos: Nienor od tego momentu nie rozumiem co sie dzieje: (2−8a²)²....... nie wiem skąd to sie wzięło .

Nienor: Wzór na Δ=b²−4ac

Bizon: ...posiał troszkę ...− 64a²

Bizon: a₁=1 a₂=−1

Bingos: Dlaczego tam jest napisane (2−8a²)² Chodzi mi o tą dwójke na początku ....

MQ: No walnął się troszkę Ma być (−8a²)²

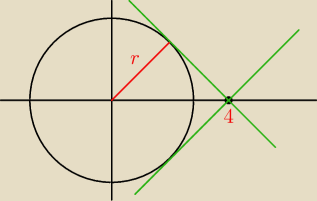
Bizon: ... zobacz jak jeszcze możesz wyznaczyć kąt nachylenia stycznej ...

Nienor: Nie wiem. Oczywiście tam ma być 64a⁴−4(1+a²)(16a²−8)=64a²−4(16a²+16a⁴−8−8a²)=64a⁴−64a²−64a⁴+32+32a²=−32a²+32 −32a²+32=0 a=1 lub a=−1 y=x−4 lub y=−x+4

Bingos: b) − tak w skrócie napisze bo nie chce mi sie pisać wszystkich obliczeń y = ax + 5 x² + (ax+5)² = 4 Δ=0 a² − 1=0 a₁ = 1 a₂ = −1 y=−x + 5 y=x + 5 tak ?

Bingos: Tam powinno być oczywiście : x² + (ax+5)² = 20

Nienor: Tak. Obliczeń mi się nie chce sprawdzać, ale o to chodzi.

Bingos: Ok spoko zrozumialem wszystko, ale proste to Uzasadnij że długość odcinka AB zawartego w stycznej do okręgu o równaniu x² + y² = 50, poprowadzonej z punktu A=(−8,10) jest równa √114. Punkt B jest punktem styczności. Takie zadanko. AB = √(x−a)²+(y−b)²−r² jest taki wzór x =−8, y=10, a=0, b=0, r²=50 podstawiam wszystko i wyjdzie √114 dobrze bedzie rozwiazane ?

Nienor: Nie ten wzór. Długość odcinka AB masz tu: https://matematykaszkolna.pl/strona/1248.html W tym zadaniu musisz policzyć wzór tej stycznej prostej (musi ona zawierać punkt A). Z układu równań (okrąg i prosta) policzyć B. Obliczyć z podanego wzoru długość AB.

Bingos: Dobra to dalej ja będe pisał taka moze kontynuacja żeby nie zakładać nowego pytania. Wyznacz drugi koniec średnicy AB okręgu wiedząc że A=(−2,4), a okrąg jest opisany równaniem (x−3)² + (y−7)² = 34