geometria analityczna matematyczna-noga: Proszę o pomoc bo rozwiązuje zadanie i w sumie nie wiem co rozwiązuje ! Punkty A=(0,3) B=(3,0) C= (5,6) i D to kolejne wierzchołki równoległoboku ,napisz równanie wysokości opuszczonej z wierzchołka D na bok AB Z góry dzięki za pomoc, mam nadzieje ,ze ktoś mi to przejżyście wyłumaczy

Basia: przerabiałeś (aś) wektory ?

matematyczna-noga: nie przerabiałem wktorów

Basia: no to beznadziejnie długie liczenie Cię czeka: 1. piszesz równanie pr.AB 2. piszesz równanie pr.CD (równoległa do AB i przechodzi przez C) 3. piszesz równanie pr.BC 4. piszesz równanie pr.AD (równoległa do BC i przechodzi przez A) 5. szukasz współrzędnych D (układ równań pr.AD i pr.CD) 6. piszesz równanie prostej DD₁ (prostopadła do AB i przechodzi przez D) 7. szukasz współrzędnych D₁ (układ równań pr.AB i pr.DD₁) 8. liczysz długość odc.DD₁

matematyczna-noga: dzięki bardzo za pomoc trochę dużo tego będzie ale teraz mam odniesienie dzięki

Bogdan:

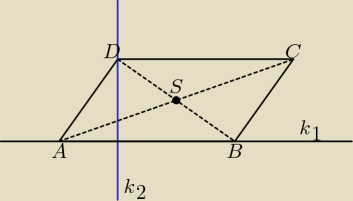
	0 + 5		5		2 + 6		9
S = (xs, ys), xs =		=		, ys =		=
	2		2		2		2

	5		3+xD		9		0+yD
D = (xD, yD),		=		⇒ xD = 2,		=		⇒ yD = 9,
	2		2		2		2

	3 − 0
k1: y = a1x + b1, a1 =		= −1
	0 − 3

k₂: y = a₂x + b₂, k₂⊥k₁ ⇒ a₁ * a₂ = −1 ⇒ a₂ = 1 k₂: y = 1(x − x_D) + y_D ⇒ y = x − 2 + 9 ⇒ y = x + 7

Mila: II sposób 1) środek AC: S(2,5;4,5) 2) D=(x,y) przekątne dzielą się na połowy S jest środkiem BD:

	x+3		y+0
(		;		)=(2,5;4,5)
	2		2

stąd x i y x=2 y=9 D(2,9) 3 ) prosta AB 4) prosta h ⊥AB i D∊h Zrób rysunek.

matematyczna-noga: dzięki bardzo

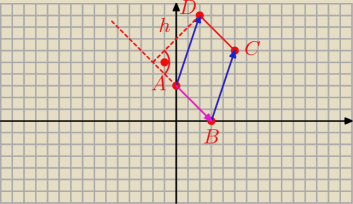
Gustlik: Basia, zamiast prowadzić kolegę krętą dróżką, pokaż wektory, tak jak ja to robię, bo bez tego będzie bryndza i recesja. Wektory są proste jak konstrukcja młotka, a znacznie skracają obliczenia. A=(0,3) B=(3,0) C= (5,6) i D=(x, y) Wektor AD^→=BC^→ BC^→=C−B=[5−3, 6−0]=[2, 6] AD^→=[2, 6] AD^→=D−A=[x−0, y−3]=[x, y−3] x=2 y−3=6 y=9 D=(2, 9) Licze wspołrzedne wektora AB^→, sa potrzebne do obliczenia współczynnika kierunkowego. AB^→=B−A=[3−0, 0−3]=[3, −3]

	−3
Wsp. kier. AB: a1=		=−1
	3

	1
Wsp. kier. prostej h: a2=−		=1
	a1

Pr. h: y=x+b Wstawiam wsp. D 9=2+b b=7 Odp: y=x+7 Naprawdę polecam wszystkim nauczyc się wektorów na własną rękę, jeżeli w szkole ich nie wytłumaczono. Co jest trudnego we wzorze AB^→=[x_B−x_A, y_B−y_A]? Nie wiem, co za idiota w MEN widział problem w wektorach, że wyciął je z programu, a potem zadanie, które można zrobic w kilku linijkach robi sie na dwie strony. To tylko odejmowanie i dodawanie, a potem zadanka z geometrii analitycznej robi sie błyskawicznie, bez zbędnych układów równań czy skomplikowanych i długich jak trasa z Warszawy do Nowego Jorku wzorów.

Eta:

Mila: Gustlik, moja droga jest prosta. Bogdana też, nie ma tam ani jednego zakrętu.

Eta: To co to za trasa? ..... bez zakrętów ?

Gustlik: Tu zadanie, które bez wektorów ja sam mając wprawę w obliczeniach robiłbym do końca świata i jeden dzień dłużej, a uczeń − nie wspomnę ile czasu by mu to zajęło: https://matematykaszkolna.pl/forum/154310.html . Proponuję przeanalizować, zwłaszcza zachęcam do tego matematyczną−nogę. To zadanie jest możliwe do rozwiązania bez wektorów, czyli po murzyńsku, nie obrazając Murzynów oczywiście, ale w każdym punkcie trzeba byłoby zaczynac obliczenia od początku, a z wektorów poszło znacznie szybciej, bo wiele wielkości można było obliczyć znając współrzędne wektorów tworzących boki trójkąta. Niemniej jednak samo w sobie zadanie jest długie, ale bez wektorów byłoby gigadługie.

Gustlik: Mila, Bogdan − tak macie rację, Wasza droga jest prosta. Niemniej gorąco zachęcam do wektorów, bo ze współrzędnych wektorów idzie naprawdę prosto obliczyc wiele innych rzeczy i bez cofania się z obliczeniami do początku, np. równanie prostej przechodzącej przez 2 punkty, odległość punktów, pola figur itp. Jak się obliczyu współrzędne wektorów to potem jest z górki, dlatego namawiam do metod wektorowych, bo są banalnie proste.

pigor: ... C=(5,6) ⇒ D=(5−3, 6+3)= (2,9), ale

	x		y
prosta AB:		+		=1 ⇔ x+y=3, więc
	3		3

z punktu D wysokość h_AB ⊥ AB ma równanie : x−y=C i 2−9=C ⇒ C=−7 i x−y=−7 ⇔ x−y+7=0 .

Gustlik: Pigor, dobry i ciekawy sposób, ale mało kto zna równanie odcinkowe prostej, a szkoda, bo jest ono bardzo proste, a na pewno prostsze od ogólnego Ax+By+C=0. Dlatego ja proponuję wektorami i równaniem kierunkowym, bo współczynnik kierunkowy łatwo się liczy z wektora, a równanie kierunkowe to zwykła funkcja liniowa, łatwe są też wzory na równoległość i prostopadłość prostych danych równaniami kierunkowymi. Pozdrawiam