 Dane są wierzchołki trójkąta ABC. A wynosi (−1,2), B(3,4), C(0,−5).
a.wyznacz rownania wszystkich prostych zawierających boki trójkąta
b napisz rownania symetralnych wszyskich boków trójkąta
c.oblicz długości boków
d. napisz równania prostych prostopadłych do boków przechodzących przez wierzchołki
e. wyznacz długości wysokości trójkąta
f. znajdź czwarty wierzchołek równoległoboku I ABCD I .
Dane są wierzchołki trójkąta ABC. A wynosi (−1,2), B(3,4), C(0,−5).
a.wyznacz rownania wszystkich prostych zawierających boki trójkąta
b napisz rownania symetralnych wszyskich boków trójkąta
c.oblicz długości boków
d. napisz równania prostych prostopadłych do boków przechodzących przez wierzchołki
e. wyznacz długości wysokości trójkąta
f. znajdź czwarty wierzchołek równoległoboku I ABCD I .
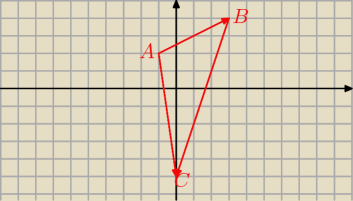 A(−1,2), B(3,4), C(0,−5)
No i tu będą potrzebne wektory.
AB→=[xB−xA, yB−yA]
Obliczmy współrzędne wszystkich wektorów stanowiących boki trójkąta:
AB→=[3−(−1), 4−2]=[4, 2]
AC→=[0−(−1), −5−2]=[1, −7]
BC→=[0−3, −5−4]=[−3, −9]
ad a)
prosta AB: − z wektora AB→=[4, 2]
A(−1,2), B(3,4), C(0,−5)
No i tu będą potrzebne wektory.
AB→=[xB−xA, yB−yA]
Obliczmy współrzędne wszystkich wektorów stanowiących boki trójkąta:
AB→=[3−(−1), 4−2]=[4, 2]
AC→=[0−(−1), −5−2]=[1, −7]
BC→=[0−3, −5−4]=[−3, −9]
ad a)
prosta AB: − z wektora AB→=[4, 2]
| 2 | 1 | |||
a1= | = | |||
| 4 | 2 |
| 1 | ||
y= | x+b | |
| 2 |
| 1 | ||
4= | *3+b | |
| 2 |
| 3 | ||
4= | +b /*2 | |
| 2 |
| 5 | ||
b= | ||
| 2 |
| 1 | 5 | |||
y= | x+ | |||
| 2 | 2 |
| −7 | ||
a2= | =−7 | |
| 1 |
| −9 | ||
a3= | =3 | |
| −3 |
| 1 | ||
a1= | ||
| 2 |
| 2+4 | ||
srodek AB S1=({−1+3}{2}, | )=(1, 3) | |
| 2 |
| 1 | ||
a2'= | ||
| 7 |
| 1 | ||
y= | x+b | |
| 7 |
| −1+0 | 2−5 | 1 | 3 | |||||
środek AC S2=( | , | )=(− | , − | ) | ||||
| 2 | 2 | 2 | 2 |
| 3 | 1 | 1 | ||||
− | = | *(− | )+b | |||
| 2 | 7 | 2 |
| 3 | 1 | |||
− | =− | +b /*14 | ||
| 2 | 14 |
| 20 | 10 | |||
b=− | =− | |||
| 14 | 7 |
| 1 | 10 | |||
y= | x− | |||
| 7 | 7 |
| 1 | ||
a3'=− | ||
| 3 |
| 1 | ||
y=− | x+b | |
| 3 |
| 3+0 | 4−5 | 3 | 1 | |||||
środek BC S3=( | , | )=( | , − | ) | ||||
| 2 | 2 | 2 | 2 |
| 1 | 1 | 3 | ||||
− | =− | * | +b | |||
| 2 | 3 | 2 |
| 1 | 1 | |||
− | =− | +b | ||
| 2 | 2 |
| 1 | ||
y=− | x | |
| 3 |

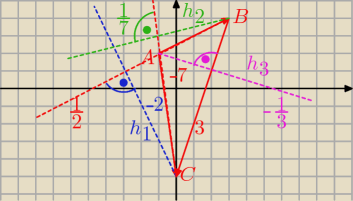 d. napisz równania prostych prostopadłych do boków przechodzących przez wierzchołki
(czyli równania wysokości trójkata)
A(−1,2), B(3,4), C(0,−5).
Liczby na rys. przy bokach i prostych oznaczają ich współczynniki kierunkowe.
Prosta h1: a=−2
y=−2x+b
wstawiam C(0,−5)
−5=−2*0+b
b=−5
y=−2x−5
d. napisz równania prostych prostopadłych do boków przechodzących przez wierzchołki
(czyli równania wysokości trójkata)
A(−1,2), B(3,4), C(0,−5).
Liczby na rys. przy bokach i prostych oznaczają ich współczynniki kierunkowe.
Prosta h1: a=−2
y=−2x+b
wstawiam C(0,−5)
−5=−2*0+b
b=−5
y=−2x−5
| 1 | ||
Prosta h2: a= | ||
| 7 |
| 1 | ||
y= | x+b | |
| 7 |
| 1 | ||
4= | *3+b | |
| 7 |
| 3 | ||
4= | +b /*7 | |
| 7 |
| 25 | ||
b= | ||
| 7 |
| 1 | 25 | |||
y= | x+ | |||
| 7 | 7 |
| 1 | ||
Prosta h3: a=− | ||
| 3 |
| 1 | ||
y=− | x+b | |
| 3 |
| 1 | ||
2=− | *(−1)+b | |
| 3 |
| 1 | ||
2= | +b /*3 | |
| 3 |
| 5 | ||
b= | ||
| 3 |
| 1 | 5 | |||
y=− | x+ | |||
| 3 | 3 |
| 1 | 5 | |||
h1 to odległość punktu C od prostej AB y= | x+ | |||
| 2 | 2 |
| 1 | 5 | |||
y= | x+ | |||
| 2 | 2 |
| 1 | 5 | |||
0= | x−y+ | /*2 | ||
| 2 | 2 |
| |0−2*(−5)+5| | 15 | 15√5 | ||||
h1= | = | = | =3√5 | |||
| √12+(−2)2 | √5 | 5 |
| |7*3+4+5| | 30 | 30 | 6 | 6√2 | ||||||
h2= | = | = | = | = | =3√2 | |||||
| √72+12 | √50 | 5√2 | √2 | 2 |
| |3*(−1)−2−5| | 10 | 10√10 | ||||
h3= | = | = | =√10 | |||
| √32+(−1)2 | √10 | 10 |
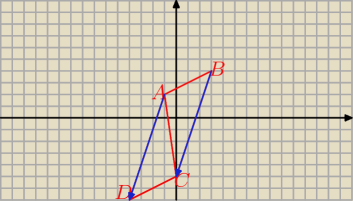 ad f. znajdź czwarty wierzchołek równoległoboku I ABCD I .
A(−1,2), B(3,4), C(0,−5) D(x, y)
Wektor AD→=BC→
BC→=[−3, −9]
AD→=[x−(−1), y−2]=[x+1. y−2]
x+1=−3
x=−4
y−2=−9
y=−7
D(−4, −7)
ad f. znajdź czwarty wierzchołek równoległoboku I ABCD I .
A(−1,2), B(3,4), C(0,−5) D(x, y)
Wektor AD→=BC→
BC→=[−3, −9]
AD→=[x−(−1), y−2]=[x+1. y−2]
x+1=−3
x=−4
y−2=−9
y=−7
D(−4, −7)
 . Jesteście przemili. A jak obliczyc dlugości wysokości trojkąta oraz znależć
czwarty wierzchołek rownoległoboku I ABCD I
. Jesteście przemili. A jak obliczyc dlugości wysokości trojkąta oraz znależć
czwarty wierzchołek rownoległoboku I ABCD I 


| yB−yA | wy | |||
a= | = | |||
| xB−xA | wx |