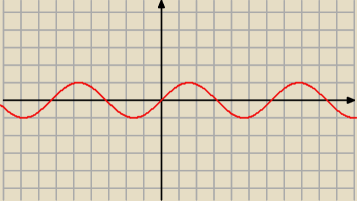
 Jest nowość. Można rysować wykresy funkcji. Kolejna innowacja. Gratuluję Jakubie
Jest nowość. Można rysować wykresy funkcji. Kolejna innowacja. Gratuluję Jakubie 
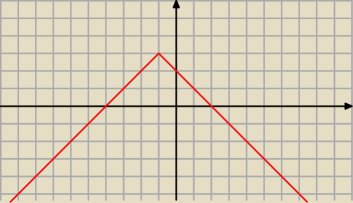
 choćby nawet do okręgów
choćby nawet do okręgów
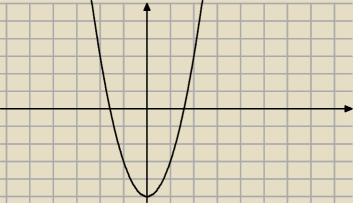 super!
super! 
 To znacznie usprawni rysowanie wykresów funkcji. Zauważyłem, że najpierw trzeba
wywołać układ współrzędnych z siatką, a potem nałożyć wykres funkcji, wykres
dopasuje się do oczek siatki.
To znacznie usprawni rysowanie wykresów funkcji. Zauważyłem, że najpierw trzeba
wywołać układ współrzędnych z siatką, a potem nałożyć wykres funkcji, wykres
dopasuje się do oczek siatki.
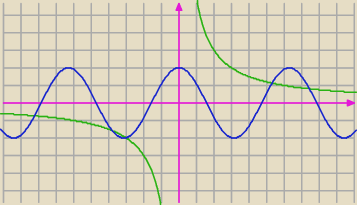
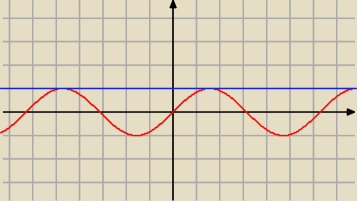 Odczytaj z wykresu ile punktów wspólnych ma prosta o równaniu y=1 z funkcją y=sinx w przedziale
(−π;π)
Odczytaj z wykresu ile punktów wspólnych ma prosta o równaniu y=1 z funkcją y=sinx w przedziale
(−π;π)  b. ELEGANCKO
b. ELEGANCKO
| 6 | ||
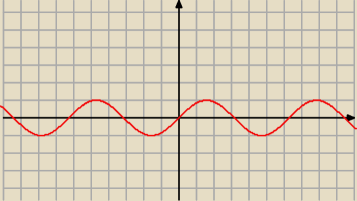
y = | i y = 2cos(x) | |
| x |

 Pozdrawiam
Pozdrawiam 








 pod pierwiastkiem masz jeszcze y
pod pierwiastkiem masz jeszcze y 


 to nawet ja umiem
to nawet ja umiem 
| 1 | ||
y = x − y ⇒ 2y = x ⇒ y = | x a tą funkcję chyba już umiesz narysować.  | |
| 2 |


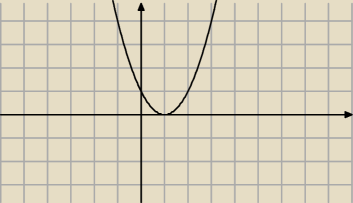 y=x2−2x+1
y=x2−2x+1
| −x2 + 5x − 3 | ||
y = | ||
| y − 8 |
 Ja chcę kółka!
Ja chcę kółka! 
 wreszcie zjarzyles
wreszcie zjarzyles 
 Bo ja nie zrozumiałem twojego postu i tak (sorki
Bo ja nie zrozumiałem twojego postu i tak (sorki  )
)

 (−2)x też nie można narysować
(−2)x też nie można narysować  Ja chcę szlaczki!
Ja chcę szlaczki!
 PS przez Ciebie ZKS mysli ze nie umiem rysowac f liniowej
PS przez Ciebie ZKS mysli ze nie umiem rysowac f liniowej 

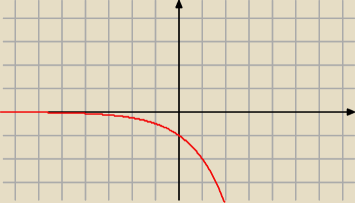



 ?
y = (−2)x
?
y = (−2)x 


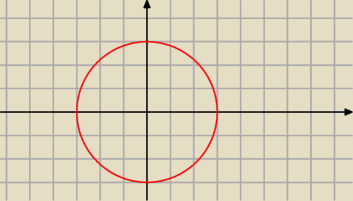


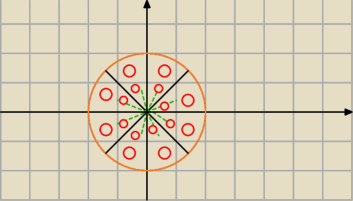
 kto zamawiał pizzę?
kto zamawiał pizzę?


 Super!
Super!

 Źle to nazwał
Źle to nazwał 

 Wykres jakiej funkcji pozwala na narysowanie takiego deseniku?
Wykres jakiej funkcji pozwala na narysowanie takiego deseniku? 

 Dziękuję za miłe słowa
Dziękuję za miłe słowa  Dodam, że wykresy można rysować i bez narysowania układu współrzędnych −− gdy nie ma
narysowanego układu, to lewy dolny róg prostokąta rysunku ma współrzędne (−3,5; −2), a prawy
górny −− (3,5; 2). Teoretycznie można to wykorzystać do rysowania ,,zwykłych'' geometrycznych
rysunków. Dziedzinę można zawęzić np. do (0,1) dodając 0*arccos(x/pi).
Jeśli chodzi o wzory typu x2+y2=9, to w ogólnym przypadku nie jest to tak prosta sprawa jak z
y=f(x) −− tutaj trzeba znajdować rozwiązania podanego równania... Dużo łatwiej byłoby dodać
rysowanie krzywych parametrycznych.
−−−−
A teraz kilka uwag ogólnych.
Bez zaglądania do kodu trudno się pewnie domyślić, jakich można używać funkcji, wypiszę je więc
tutaj. Oto nazwy funkcji jednej zmiennej:
'sin', 'cos', 'tg', 'ctg', 'arcsin', 'arccos', 'arctg', 'arcctg', 'exp', 'ln', 'log', 'sinh',
'cosh', 'tgh', 'ctgh', 'abs', 'sqrt', 'p', 'p2', 'p3', 'p4', 'p5', 'p6', 'p7', 'p8', 'p9'
I jedyna funkcja dwóch zmiennych: 'u', 'U' (występująca pod dwoma nazwami), oznaczająca ułamek:
u(x,y)=x/y.
Do tego dochodzą standardowe działania: +−*/^, oraz standardowa notacja np. '|x+3|' na wartość
bezwzględną.
Są dwie zdefiniowane stałe: 'e' oraz 'pi'.
Par nawiasów {} oraz () można używać wymiennie. Np. 'sin(2x)' daje taki sam efekt jak 'sin{2x}'
Dodam, że wykresy można rysować i bez narysowania układu współrzędnych −− gdy nie ma
narysowanego układu, to lewy dolny róg prostokąta rysunku ma współrzędne (−3,5; −2), a prawy
górny −− (3,5; 2). Teoretycznie można to wykorzystać do rysowania ,,zwykłych'' geometrycznych
rysunków. Dziedzinę można zawęzić np. do (0,1) dodając 0*arccos(x/pi).
Jeśli chodzi o wzory typu x2+y2=9, to w ogólnym przypadku nie jest to tak prosta sprawa jak z
y=f(x) −− tutaj trzeba znajdować rozwiązania podanego równania... Dużo łatwiej byłoby dodać
rysowanie krzywych parametrycznych.
−−−−
A teraz kilka uwag ogólnych.
Bez zaglądania do kodu trudno się pewnie domyślić, jakich można używać funkcji, wypiszę je więc
tutaj. Oto nazwy funkcji jednej zmiennej:
'sin', 'cos', 'tg', 'ctg', 'arcsin', 'arccos', 'arctg', 'arcctg', 'exp', 'ln', 'log', 'sinh',
'cosh', 'tgh', 'ctgh', 'abs', 'sqrt', 'p', 'p2', 'p3', 'p4', 'p5', 'p6', 'p7', 'p8', 'p9'
I jedyna funkcja dwóch zmiennych: 'u', 'U' (występująca pod dwoma nazwami), oznaczająca ułamek:
u(x,y)=x/y.
Do tego dochodzą standardowe działania: +−*/^, oraz standardowa notacja np. '|x+3|' na wartość
bezwzględną.
Są dwie zdefiniowane stałe: 'e' oraz 'pi'.
Par nawiasów {} oraz () można używać wymiennie. Np. 'sin(2x)' daje taki sam efekt jak 'sin{2x}'
| 1 | ||
Można używać notacji podobnej jak w edytorze, np. U(1)(2+3x) na | ||
| 2+3x |
 ). Dzięki temu można wkleić wpisany wzór z edytora do okienka na wzór i na
ogół rysowanie wykresu zadziała.
Można używać skróconej notacji, np. 'sin x', ale tylko wtedy, gdy argumentem funkcji jest
pojedyncza zmienna. Np. 'sin x' jest OK, ale 'sin 2x' lub 'sin 2' nie.
Poprawne jest też np. 'sin x^2', ale jest interpretowane jako (sin x)2
Zmienną nie musi być x, zmienną może być jakikolwiek napis (pod warunkiem, że nie jest on nazwą
funkcji lub stałej, czyli np. 'e', 'p' i 'u' są zabronione), ale we wzorze może być tylko
jedna zmienna (wykresów funkcji 2 zmiennych nie da się rysować).
Np. '2+3y' da taki sam efekt jak '2+3x' albo '2+3*zmienna'.
Z kolei 'x+t' da błąd.
W tej chwili nie ma wygodnej metody obcinania dziedziny. Można sobie jednak poradzić np.
dodając 0*arcsin(...) i wpisując odpowiednie wyrażenie pod ...
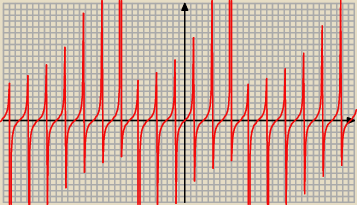
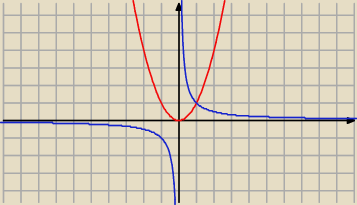
Rysunki bywają brzydkie, gdy funkcja ma asymptotę. Dla przykładu u góry brzydki rysunek y=tg x.
Ten akurat rysunek da się poprawić przez wybranie wiekszej kratki.
Uwagi dla programistów: wzór '2*−3' jest niepoprawny. Wzór '1e+9' jest poprawny, ale
interpretowany jako '1*e + 9'
). Dzięki temu można wkleić wpisany wzór z edytora do okienka na wzór i na
ogół rysowanie wykresu zadziała.
Można używać skróconej notacji, np. 'sin x', ale tylko wtedy, gdy argumentem funkcji jest
pojedyncza zmienna. Np. 'sin x' jest OK, ale 'sin 2x' lub 'sin 2' nie.
Poprawne jest też np. 'sin x^2', ale jest interpretowane jako (sin x)2
Zmienną nie musi być x, zmienną może być jakikolwiek napis (pod warunkiem, że nie jest on nazwą
funkcji lub stałej, czyli np. 'e', 'p' i 'u' są zabronione), ale we wzorze może być tylko
jedna zmienna (wykresów funkcji 2 zmiennych nie da się rysować).
Np. '2+3y' da taki sam efekt jak '2+3x' albo '2+3*zmienna'.
Z kolei 'x+t' da błąd.
W tej chwili nie ma wygodnej metody obcinania dziedziny. Można sobie jednak poradzić np.
dodając 0*arcsin(...) i wpisując odpowiednie wyrażenie pod ...
Rysunki bywają brzydkie, gdy funkcja ma asymptotę. Dla przykładu u góry brzydki rysunek y=tg x.
Ten akurat rysunek da się poprawić przez wybranie wiekszej kratki.
Uwagi dla programistów: wzór '2*−3' jest niepoprawny. Wzór '1e+9' jest poprawny, ale
interpretowany jako '1*e + 9'  To chyba tyle. Miłego rysowania!
To chyba tyle. Miłego rysowania! 
 a to
a to  ?
?



 Może by Jakubie dodać przy textboxie z listą dostępnych funkcji. Coś na wzór "Kliknij po więcej
przykładów".
Zmiany na forum bardzo na plus.
Może by Jakubie dodać przy textboxie z listą dostępnych funkcji. Coś na wzór "Kliknij po więcej
przykładów".
Zmiany na forum bardzo na plus. 

 To super sprawa
To super sprawa  ! Fajna rzecz z tymi funkcjami − b, Jakubie serdeczne dzięki
! Fajna rzecz z tymi funkcjami − b, Jakubie serdeczne dzięki  !
!
 P.S Spacja się nie wcisnęła
P.S Spacja się nie wcisnęła
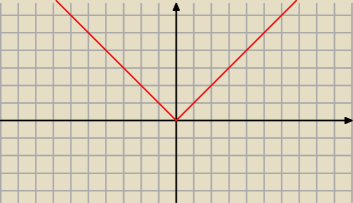
 dla Gustliczka
dla Gustliczka 
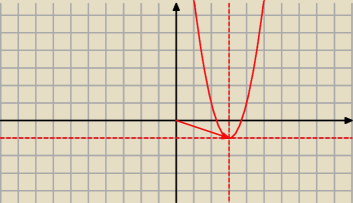 Postać kanoniczna funkcji kwadratowej − przesuwanie paraboli
y=2x2 T w→=[3, −1] ⇒ y=2*(x−3)2−1
Postać kanoniczna funkcji kwadratowej − przesuwanie paraboli
y=2x2 T w→=[3, −1] ⇒ y=2*(x−3)2−1

 ! Pozdrawiam
! Pozdrawiam  Tak sobie sprawdzam rysowanie wykresów funkcji − bardzo fajna i pożyteczna rzecz.
Tak sobie sprawdzam rysowanie wykresów funkcji − bardzo fajna i pożyteczna rzecz.
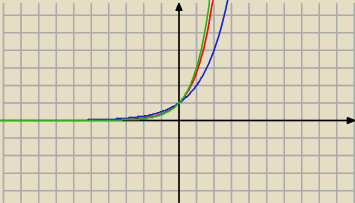 y=2x
y=ex
y=3x
y=2x
y=ex
y=3x
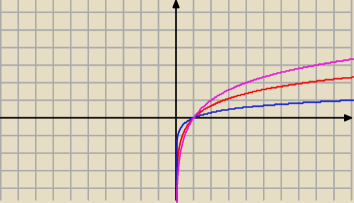 y=logx
y=lnx
y=log2x
Funkcje logarytmiczne:
logarytm dziesiętny
y=logx wpisujemy y=log(x)
logarytm naturalny
y=lnx wpisujemy y=ln(x)
logarytm o dowolnej podstawie
y=logx
y=lnx
y=log2x
Funkcje logarytmiczne:
logarytm dziesiętny
y=logx wpisujemy y=log(x)
logarytm naturalny
y=lnx wpisujemy y=ln(x)
logarytm o dowolnej podstawie
| logbx | ||
y=logax korzystamy ze wzpru na zmianę podstawy logarytmu logax= | ||
| logba |
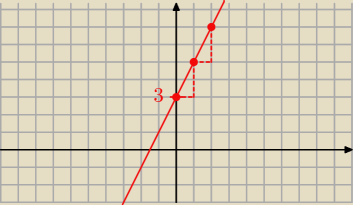 Metoda "schodkowa" rysowania wykresów funkcji liniowej. Na rys. funkcja y=2x+3.
Metoda "schodkowa" rysowania wykresów funkcji liniowej. Na rys. funkcja y=2x+3.
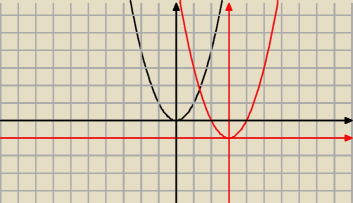 Dwa wykresy na jednym rysunku przesunięte wzgledem siebie, funkcja y=x2.
Dwa wykresy na jednym rysunku przesunięte wzgledem siebie, funkcja y=x2.

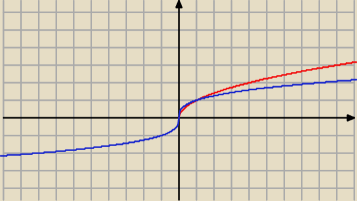 Pierwiastki
y=√x wpisujemy y=p(x)
y=3√x wpisujemy y=p3(x)
Pierwiastki
y=√x wpisujemy y=p(x)
y=3√x wpisujemy y=p3(x)
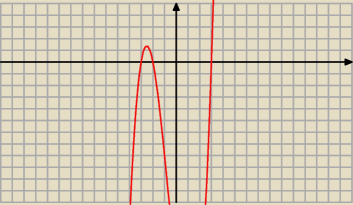 Wielomian
y=x3+2x2−9x−18
Wielomian
y=x3+2x2−9x−18
 ale w sumie taka instrukcja jak wprowadzac funkcje
ale w sumie taka instrukcja jak wprowadzac funkcje 
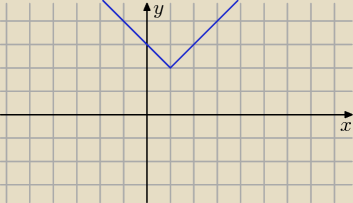 y=|x−1|+2
y=|x−1|+2
 W sumie mogłem sytać o wektor przesunięcia
W sumie mogłem sytać o wektor przesunięcia  .
.
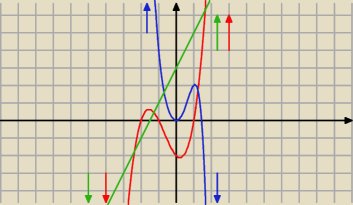 TO MOŻE UŁATWIĆ ROZWIAZYWANIE NIERÓWNOŚCI WIELOMIANOWYCH I SPRAWDZENIE, CZY WYKRES JEST DOBRZE
NARYSOWANY
TO MOŻE UŁATWIĆ ROZWIAZYWANIE NIERÓWNOŚCI WIELOMIANOWYCH I SPRAWDZENIE, CZY WYKRES JEST DOBRZE
NARYSOWANY  !
Ciekawa własność wielomianów − wielomiany stopni nieparzystych mają "ramiona" wykresów
skierowane w przeciwne strony − jedno ramię w górę a drugie w dół. Jest to analogia do funkcji
liniowej.
Prawe ramię zawsze zachowuje się jak ramiona paraboli niezależnie od stopnia wielomianu i jego
parzystości − współczynnik "kierunkowy" (czyli a − pierwszy wyraz wielomianu) dodatni − prawe
ramię w górę, współczynnik "kierunkowy" a ujemny − prawe ramię w dół.
Na rysunku
y=2x+3
y=x3+2x*2−x−2
y=−x5+3x2
!
Ciekawa własność wielomianów − wielomiany stopni nieparzystych mają "ramiona" wykresów
skierowane w przeciwne strony − jedno ramię w górę a drugie w dół. Jest to analogia do funkcji
liniowej.
Prawe ramię zawsze zachowuje się jak ramiona paraboli niezależnie od stopnia wielomianu i jego
parzystości − współczynnik "kierunkowy" (czyli a − pierwszy wyraz wielomianu) dodatni − prawe
ramię w górę, współczynnik "kierunkowy" a ujemny − prawe ramię w dół.
Na rysunku
y=2x+3
y=x3+2x*2−x−2
y=−x5+3x2
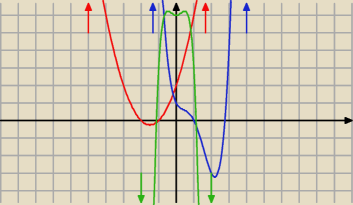 A tak zachowują się wykresy wielomianów stopni parzystych − oba ramiona w tę samą stronę albo w
górę (gdy a>0) albo w dół (gdy a<0) − jak parabola, a oznacza oczywiście współczynnik
"kierunkowy", czyli pierwszy wyraz wielomianu.
y=x2+3x+2
y=x4−4x3+4x2−2x+1
y=−x6−4x4+2x2+6
A tak zachowują się wykresy wielomianów stopni parzystych − oba ramiona w tę samą stronę albo w
górę (gdy a>0) albo w dół (gdy a<0) − jak parabola, a oznacza oczywiście współczynnik
"kierunkowy", czyli pierwszy wyraz wielomianu.
y=x2+3x+2
y=x4−4x3+4x2−2x+1
y=−x6−4x4+2x2+6
 .
.
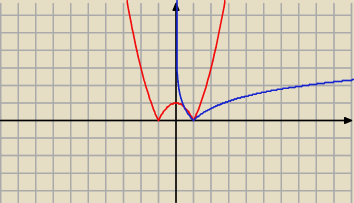 Funkcje z wartościami bezwzględnymi:
y=|x2−1|
y=|lnx|
Funkcje z wartościami bezwzględnymi:
y=|x2−1|
y=|lnx|
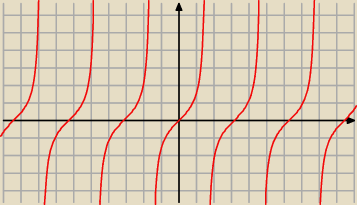 y=tgx
y=tgx
 Dobre
Dobre 
 Miodzio,miodzio,miodzio
Miodzio,miodzio,miodzio  Wreszcie nie będzie problemów z rysowaniem wykresów wielomianów
Wreszcie nie będzie problemów z rysowaniem wykresów wielomianów 

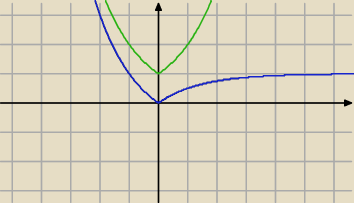
 leniwa się zrobiłam, to przecież łatwo rozpisać na dwie funkcje i gotowe
leniwa się zrobiłam, to przecież łatwo rozpisać na dwie funkcje i gotowe
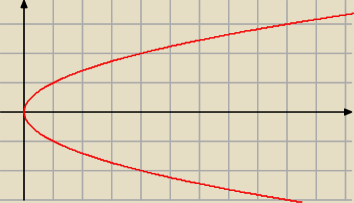
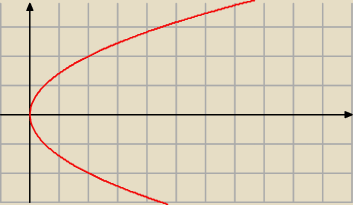 dlaczego miałyby się nie złączyć ?
to jest właśnie tak narysowane
dlaczego miałyby się nie złączyć ?
to jest właśnie tak narysowane
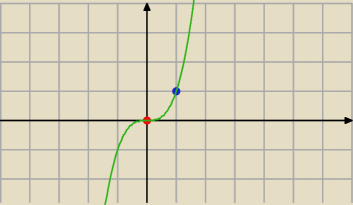 najpierw kratki
ostatnia ikona w środkowym rzędzie
dwa kliki; pierwszy: początek układu; drugi: pierwszy punkt kratowy
kropki pokazują gdzie kliknęłam
dopiero potem wykres
najpierw kratki
ostatnia ikona w środkowym rzędzie
dwa kliki; pierwszy: początek układu; drugi: pierwszy punkt kratowy
kropki pokazują gdzie kliknęłam
dopiero potem wykres
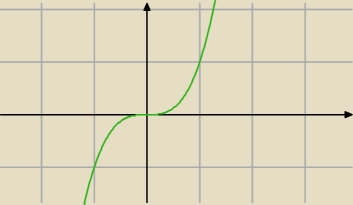 P.S. wykres jest mądry; sam dopasuje się do kratek
P.S. wykres jest mądry; sam dopasuje się do kratek
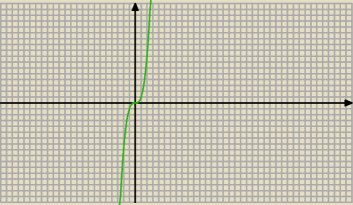
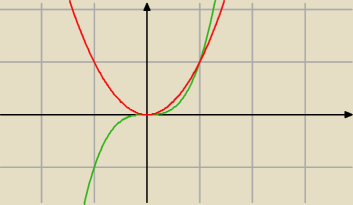 y = x3
y = x2
jeszcze większa skala byłaby wskazana
y = x3
y = x2
jeszcze większa skala byłaby wskazana
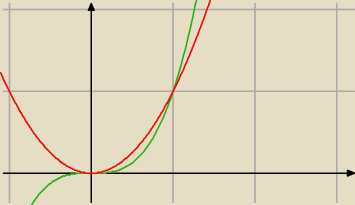 teraz już dobrze widać co i jak
teraz już dobrze widać co i jak
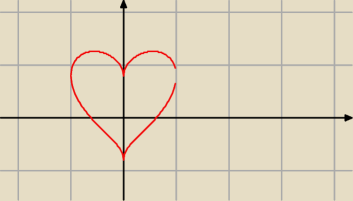 dla Basi
dla Basi 