najwieksza i najmniejsza wartosc w przedziale ewelka: mialam obl najw i najm wartosc funkcji w przedziale [0,2] f(x)=−x⁴+6x³−4x²−2 wyszlo ze najmniejsza = −2 w x=0 a najwieksza =46 w x=2 dobrze czy zle ?

ZKS: A liczone były ekstrema?

Basia: niestety źle napisz najpierw jak policzyłaś pochodną

ewelka: aa czyli najpierw liczymy pochodna i pod nia podstawiamy te punkty ? pochodna = 4x³−18x²−8x

ZKS: Najpierw liczysz ekstremum funkcji.

Basia: nic nie podstawiamy szukamy ekstremów i patrzymy czy któreś należy do zadanego przedziału gdyby żadne nie należało to zdecydują wartości funkcji na końcach przedziału, ale dopiero wtedy

ewelka: a moglabys mi to rozwiazac , pokazac jak co po kolei ? bardzo bym byla wdzieczna..

Ajtek: Błędnie policzona pochodna: f'(x)=−4x³+18x²−8x

ewelka: ajj tak, zle popatrzylam na znaki,, i co dalej z tym robic ?

ZKS: Zobacz tutaj jak policzyć ekstremum i jak sprawdzać czy jest to minimum czy maksimum 387.

Basia: pochodną źle policzyłaś f(x) = −x⁴+6x³−4x²−2 f'(x) = −4x³+18x²−8x = −2x(2x²−9x+4) = −2x*2(x−¹₂)(x−4) = −4x(x−¹₂)(x−4) rysujesz sobie wykres i masz x∊(−∞;0) ⇒ f'(x)>0 ⇒ f.rośnie x∊(0;¹₂) ⇒ f'(x)<0 ⇒ f.maleje x∊(¹₂;4) ⇒ f'(x)>0 ⇒ f.rośnie x∊(4;+∞) ⇒ f'(x)<0 ⇒ f.maleje czyli: x_max1 = 0

	1
xmin =
	2

x_max2 = 4 Twój przedział to [0;2] czyli x_min do niego należy czyli wartością najmniejszą jest f(¹₂) to już sobie policz natomiast wartość największa to albo f(0), albo f(2) (albo obie, bo mogą być równe) trzeba policzyć i porównać

Ajtek: Basia miałaś oczywiście na myśli "x_max2 do niego nie należy" .

Basia: nic nie piszę o x_max2, a to, że x_max1=0∊[0;2] nie przesądza o wartości największej w tym przedziale

Ajtek: Przepraszam, nie doczytałem dokładnie.

ewelka: okej. tylko ja nie rozumiem dlaczego np w przedziale (0,1/2) maleje funkcja jak i od (4,+niesk)

Basia: narysuj wykresy: y = −4x y = x − ¹₂ y = x−4 poprowadź proste pomocnicze przez miejsca zerowe i patrz co jest w kolejnych przedziałach dodatnie, a co ujemne kolejno będzie: (+)*(+)*(+) = (+) (−)*(+)*(+) = (−) (−)*(−)*(+) = (+) (−)*(−)*(−) = (−)

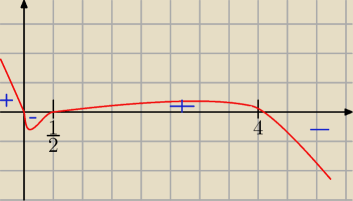
Aga1.: Oto wykres pochodnej. f(x)maleje w przedziałach, gdzie pochodna przyjmuje wartości ujemne.

ewelka: kurde tak tego nie zrozumiem w sensie ten y=−4, y=x−1/2 , nie wiem nadal , przykro mi a jak policzyc ktora jest najwieksza ? podstawic pod pochodna wyliczona czy jak ?

ewelka: dziekuje za ten wykres ! pomogl mi !

ewelka: tylko z tymi wartosciami jeszcze ktora czy 0 czy 2 bedzie najwieksza , jak policzyc?

ZKS: Wstawiasz w miejsce x odpowiednio 0 a później 2 i sprawdzasz która wartość jest większa.

ewelka: ale do pochodnej czy do funkcji podtsawowej ?

ZKS: Do funkcji bo musisz sprawdzić jej wartości w danych punktach.

ewelka: wyszlo ze w dla x=0 wyszlo 2, a dla x=2 wyszlo 22 wiec najw bedzie w x=2