pochodna nataszka15: jak obl z tego pochodna? wzor f(x)=f'g*fg' tylko pochodna z 'e^−x to jest e^x? f(x)=e^x+e^−x

nataszka15: wzor f(x)= f'g+fg', pomylke tam zrobilam

Artur_z_miasta_Neptuna: (e^−x)' = −e^−x moja droga

Artur_z_miasta_Neptuna: jak już to (f*g)' = f' * g + f * g' a mając (f(x) + g(x) )' = f' + g'

nataszka15: i korzystam ze wzoru f(x)= f' +g' ?

Artur_z_miasta_Neptuna: https://matematykaszkolna.pl/strona/359.html zapraszam do zapoznania się

nataszka15: wlasnie o to mi chodzilo, dziekuje, nie na ten przyklad spojrzalam

Artur_z_miasta_Neptuna: a jak wygląda wzór funki h(x) = f(x) + g(x) = e^x + e^−x ... a więc ... tak, z tego korzystasz

nataszka15: czyli wyszlo ze pochodna wynosi e^x−e^−x. Jak mam okreslic monotonicznosc tej funkcji?

nataszka15: wzor wyglada tak: f(x)= e^x+e^−x

Artur_z_miasta_Neptuna: monotoniczność 1) badasz czy pochodna ma miejsca zerowe. 2) wyznacz te miejsca 3) szkicujesz wykres f' 4) na podstawie wykresu odczytujesz monotoniczność funkcji f(x)

nataszka15: mam w odp tak ,ze : D = R, f malejaca w (−niesk, 0), f rosnaca w (0,niesk), f min.lok w x = 0 równe 2. nie wiem skad sie np tak 2 wziela i w ogole

Artur_z_miasta_Neptuna: f posiada minimum lokalne w x=0 równe 2 ....... czyli: funkcja przyjmuje minimum lokalne dla x₀=0 a wartość funkcji w tym punkcie wynosi 2 ... czyli f(0) = 2

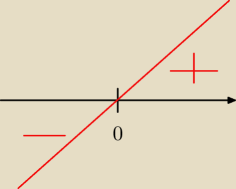
Artur_z_miasta_Neptuna: 1)

	1
ex − e−x = 0 ⇔ ex = e−x ⇔ ex =		⇔ e2x = 1 ⇔ e2x = e0 ⇔ 2x=0 ⇔ x=0
	ex

2) x=0 3) patrz rysunek 4) f'>0 ⇒ f↗ w (0 ; +∞) f'<0 ⇒ f↘ w (−∞ ; 0) f(0) = e⁰ + e⁻⁰ = 1+1 = 2

nataszka15: dziekuje Ci jestes wielki