tryg
bumblebee: Mam otóż problem takiej natury, że jestem w stanie bez problemu rozwiazac wiekszosc rownan
trygonometrycznych, ale klopotow nastrecza mi napisanie odpowiedzi... czy moglby mi ktos
wytlumaczyc po kolei malymi kroczkami jak dziecku

co i jak, np na tym przykladzie

(2sin
2x−1)(sinx+1)=0, dla x nalezacego do <0, 2π>
3 maj 17:43
bumblebee: ja bym to napisal tak, ze:
| | √2 | | √2 | |
sinx= |
| ⋁ sinx=− |
| ⋁ sinx=−1 |
| | 2 | | 2 | |
no i co dalej


3 maj 17:45
bumblebee: | | π | | π | | 3π | |
czyli x= |
| +2kπ v x=− |
| +2kπ v x= |
| , czy tak  no ale wiem ze to nie wsyzstko bo |
| | 4 | | 4 | | 2 | |
trzeba jeszcze ustalic z tego miejsca zerowe z przedzialu ktory mamy dany..
3 maj 17:48
@Basia:
Musisz sobie naszkicować (albo jeszcze lepiej znaleźć dobrze narysowany) wykres danej
f.trygonometrycznej. W tym wypadku sinusa. W przedziale <0;2π>
Jeżeli przez punkt (
π4;
√2/2) poprowadzisz prostą równoległą do OX zobaczysz, że
przecina ona wykres sinusa w jeszcze jednym punkcie.
Ten punkt to π−
π4 =
3π4, bo wykres sinusa w <0;π> jest symetryczny względem prostej
x =
π2.
To wynika także z wzorów redukcyjnych:
sin(π−x) = sinx ⇒
sin
π4 =
√2/2 to sin
π4 = sin(π−
π4) = sin
3π4 =
√2/2
Patrzysz teraz na przedział <π;2π>
−
√2/2 sinus przyjmie dla
π+
π4 i π+
3π4
czyli dla
x =
5π4 i x=
7π4
To też wynika z wzorów redukcyjnych:
sin(x+π) = −sinx
Ale pamiętanie o wzorach redukcyjnych jest trudne.
Lepiej nauczyć się szybkiego szkicowania wykresu w przedziale <0;2π> i odczytywania z niego
tych wartości tak jak opisałam.
Wiem, że to może nie być całkiem jasne. Szczególnie bez rysunku.
Dlatego najpierw wykres.
3 maj 18:14
Jakub: Dobrze napisałeś te równania z sinusami tylko, nie do końca dobrze rozwiązałeś;
| | π | | π | | 3π | |
x = |
| ∨ x = π− |
| = |
| |
| | 4 | | 4 | | 4 | |
| | π | | 5π | | π | | 7π | |
x = π + |
| = |
| ∨ x = 2π − |
| = |
| |
| | 4 | | 4 | | 4 | | 4 | |
sin x = −1
| | √2 | |
Narysuj sobie wykres sinusa i następnie patrz, gdzie przyjmuje wartości |
| , |
| | 2 | |
| | √2 | |
− |
| , −1. Tylko uważaj, aby się ograniczać tylko do przedziału <0,2π>. |
| | 2 | |
Rozwiązywanie równań trygonometrycznych z wykresem jest najprostsze. W ogóle poczytaj
rozwiązania tych zadań
1578. Powodzenia.
3 maj 18:19
Jakub: No to myślimy Basia tak samo

3 maj 18:20
Bogdan:
Dobry wieczór.
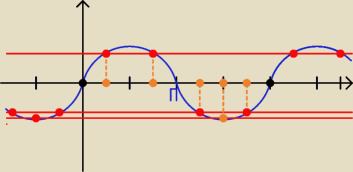
Dobrze rozwiązałeś. Trzeba dobrać takie k, aby rozwiązania zawarły się w podanym
przedziale, można je zobaczyć na rysunku.
(2sin
2x − 1)(sinx + 1) = 0, dla x należącego do <0, 2π>
| | 1 | |
2(sin2x − |
| )(sinx + 1) = 0 |
| | 2 | |
| | √2 | | √2 | |
2(sinx − |
| ) (sinx + |
| ) (sinx + 1) = 0 |
| | 2 | | 2 | |
| | √2 | | −√2 | |
sinx = |
| lub sinx = |
| lub sinx = −1. |
| | 2 | | 2 | |
| | π | | 3π | | 5π | | 3π | | 7π | |
Dla x ∊ <0, 2π> x ∊ { |
| , |
| , |
| , |
| , |
| } |
| | 4 | | 4 | | 4 | | 2 | | 4 | |
Na rysunku niebieska linia to wykres y = sinx,
| | √2 | |
górna czerwona linia to wykres y = |
| , |
| | 2 | |
| | −√2 | |
poniżej kolejna czerwona linia to wykres y = |
| , |
| | 2 | |
najniższa czerwona linia to wykres y = −1
3 maj 18:30
Bogdan:
Witam Basiu i Jakubie. Miłego wieczoru życzę.
3 maj 18:33
bumblebee: ok dziekuje za wytlumaczenie, teraz to tylko musze przeanalizowac

3 maj 18:37
bumblebee: kurcze wszystko rozumiem

3 maj 18:52
 co i jak, np na tym przykladzie
co i jak, np na tym przykladzie (2sin2x−1)(sinx+1)=0, dla x nalezacego do <0, 2π>
(2sin2x−1)(sinx+1)=0, dla x nalezacego do <0, 2π>


 no ale wiem ze to nie wsyzstko bo
no ale wiem ze to nie wsyzstko bo
 Dobry wieczór.
Dobrze rozwiązałeś. Trzeba dobrać takie k, aby rozwiązania zawarły się w podanym
przedziale, można je zobaczyć na rysunku.
(2sin2x − 1)(sinx + 1) = 0, dla x należącego do <0, 2π>
Dobry wieczór.
Dobrze rozwiązałeś. Trzeba dobrać takie k, aby rozwiązania zawarły się w podanym
przedziale, można je zobaczyć na rysunku.
(2sin2x − 1)(sinx + 1) = 0, dla x należącego do <0, 2π>

