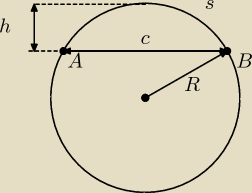
Pilne zadanie na okręgu Jacek: Potrzebuję obliczyć dane okręgu odcinek "s" (po okręgu, pomiędzy punktami A i B) i promień "R". Posiadam dane: h=30 c=250 Pozdrawiam

Artur_z_miasta_Neptuna:

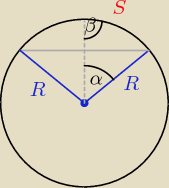
	c   2		125		25		25
tgβ =		=		=		⇒ arctg(		) = 76,5o
	h		30		6		6

2β = 2* 76,5^o = 153^o 360−2α = 2*(2β) = 306^o ⇔ 2α = 54^o ⇔ α = 27^o

	27
a więc ... 's' to jest 2πR*		= ....
	360

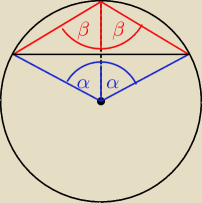
Artur_z_miasta_Neptuna: chyba że 'S jest lukiem o kącie 2α ... to odpowiednio 2* to co wyszło wyżej

	54
czyli 2πR*		= ...
	360

Artur_z_miasta_Neptuna:

Jacek: Artur ja się kompletnie w tym nie orientuję

Artur_z_miasta_Neptuna: obliczasz kąt β ... korzystając z arctg zauważasz ... że górny trójkąt (czerwone ramiona) to trójkąt równoramienny korzystasz z tw. o kącie opartym na tym samym łuku: https://matematykaszkolna.pl/strona/465.html stąd wyznaczasz 360−2α = 2* (2β) stąd wyznaczasz 2α a następnie wyznaczasz długość łuku S: https://matematykaszkolna.pl/strona/474.html

Jacek: muszę to to chyba kilka razy przerobić żeby zrozumieć

Jacek: a jak obliczyć średnicę?

Artur_z_miasta_Neptuna: pisałeś, że 'posiadam dane: h = 30 c = 250' !

Jacek: tak potrzebuję dokładnie obliczyć średnicę okręgu oraz odcinek s mając dane j.w.

Jacek: h=30mm s=250mm

Artur_z_miasta_Neptuna: skoro masz wyznaczone 2α ... to wyznaczasz α.

	c   2		125
sin α =		⇔ R =		= ....
	R		sin 27o

i już masz promień

Jacek: czyli wychodzi mi, że R wynosi ≈275,34

Artur_z_miasta_Neptuna: tak

Jacek: pierdoły wychodzą mi przy s mianowicie ≈23,06, a przecież wiem, że ten łuk jest dłuży niz c które wynosi 30

Artur_z_miasta_Neptuna: http://www.wolframalpha.com/input/?i=2pi*%28125%2Fsin27%29*54%2F360 pozdrawiam

pigor: mnie te z to wychodzi , coś tu nie gra mi z danymi , albo ja jestem taki głupi, bo z tw. Pitagorasa : (R−30)²+(¹₂*250)²=R² ⇒ R≈ 275,41 > c=250 kto mi powie co jest grane

pigor: a już wiem , zasugerowałem się rysunkiem po prostu h w stosunku do c jest małe , wtedy jest o. k. , czyli to R jest dobre , no to dalej np. z tw. cosinusów jeśli α − miara ką środkowego opartego na tym łuku

	2R2−c2		c2
to cosα=		= 1−		≈ 1−0,4120= 0,5880 ⇒ α ≈ 0,9422 (w radianach) ,
	2R2		2R2

zatem s=α*R = 0,9422 *275,41 ≈ 259,5 . ...

pigor: nawet wygląda ten wynik na przyzwoity (możliwy , ) ale niech ktoś sprawdzi, bo mogłem się walnąć. ...

Jacek: s może wynieść 25,95 i z tym bym się zgodził

Artur_z_miasta_Neptuna: Jacek −−−− jak S może wynieść 1/10 prostej na której ten łuk jest oparty zastanów się .... odcinek |AB| = 250 ... więc łuk |AB| musi być większy −−− nie ma tutaj zakrzywiania czasoprzestrzeni Pigor −−− wyszło mi tyle samo (kwestia zaokrągleń)

Artur_z_miasta_Neptuna: Jacek −−− przesuń przecinek i będziesz miał prawidłowy wynik

Jacek: to fakt