zadania
Saizou : to może jakieś zadanko na późne przedpołudnie

1 sie 11:39
Saizou : poziom rozszerzony kl I LO
1 sie 11:42
Artur_z_miasta_Neptuna:
Saizou −−− Ty jesteś chyba jakiś niewyżyty

1 sie 11:44
Artur_z_miasta_Neptuna:
Krzysiek zaraz wrzuci swoje zadania (patrz jego temat) ... to będziesz miał
1 sie 11:44
Saizou : trochę, trzeba się dokształcić żeby dobrze napisać maturę za 2 lata im wcześniej się zacznie
naukę tym więcej zadań się przeliczy i będzie się miało większą wiedzę

1 sie 11:51
Mila: Sześcian o krawędzi 10 cm pomalowano na czerwono a następnie rozcięto na sześcianiki
jednostkowe.
Oblicz ile sześcianików ma pomalowane na czerwono:
a) 3 scianki
b) 2 ścianki
c) jedną ściankę.
1 sie 16:46
AS:
1. Rozwiązać układ równań
| x*y | | 12 | | y*z | | 18 | | z*x | | 36 | |
| = |
| , |
| = |
| , |
| = |
| |
| x + y | | 5 | | y + z | | 5 | | z + x | | 13 | |
2. Uprość wyrażenie
(a + b − c)
3 + (b + c − a)
3 + (c + a − b)
3 − (a + b + c)
3
3. Zbudować konstrukcyjnie trójkąt, mając dane jego obwód
i dwa kąty wewnętrzne.
1 sie 17:01
Saizou : yyy co to jest sześcian jednostkowy

1 sie 17:13
picia:
mysle ze 1x1x1

1 sie 17:14
Mila: Sześcian o krawędzi 1cm.
1 sie 17:14
Patryk: a) 8 ?
1 sie 17:21
Saizou :
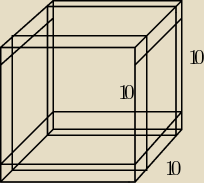
wszystkich sześcianów jednostkowych jest
v=10*10*10=1000
zauważmy, że dwie ściany pomalowane będzie miał sześcian który jest stworzony ze styku ścian:
zatem
−na przedniej ścianie jest ich:32
− na ścianie z tyłu : 32
− na prawej 16
− na lewej 16
−na górnej 0
na dolnej 0 , wówczas sześcianów pomalowanych na dwóch stron jest 96
pomalowanych z jednej strony będzie:
8*8*6=384
a pomalowanych z trzech stron będzie 8
1 sie 17:27
Mila: a) 8 (wierzchołkowe sześcianiki)
b) 12*8=96 ( na każdej krawędzi 8)
c) 6*(8*8)=384
Bardzo ładnie, Błażej(?) jesteś myślącym licealistą.
1 sie 17:36
Saizou : o widzę że się po troszku sławny staję na tym forum

zadanie było proste jak ktoś ma dobre wyobrażenie przestrzenne
1 sie 17:42
Saizou : układ równań ma rozwiązanie: x=4 y=6 z=9
1 sie 20:00
Saizou : a uproszczenie to: −24abc
1 sie 20:02
Saizou : to co ciąg dalszy zmagań


2 sie 20:00
AS:
1. Wykazać,że jeśli a,b,c są miarami boków trójkąta prostokątnego
o przeciwprostokątnej c, to równanie x2 − 2*(a2 + b2) + c4 = 0
ma tylko jeden pierwiastek podwójny.
2. Wykazać,że jeżeli a,b,c są miarami boków trójkąta rozwartokątnego
w którym c leży naprzeciw kąta rozwartego,to równanie
x2 − 2*c*x + a2 + b2 = 0 ma dwa pierwiastki dodatnie.
3. Ile wynosi iloczyn pierwiastków równania dwukwadratowego
a*x4 + b*x2 + c = 0 w którym b2 − 4*a*c > 0.
2 sie 20:21
Saizou : w tym pierwszym dochodzę do momentu
x2−c2(2+c2)=0 i dalej nie wiem co mam zrobić, może jakaś podpowiedź
2 sie 20:32
Saizou : x2=c2(2+x2)
lxl=c√2+x2
zatem równanie ma jeden pierwiastek podwójny
2 sie 20:34
Saizou : 3/
t=x
2, t∊C
at
2+bt+c=0
zatem że delta jest większa od zera możemy zastosować wzory Viete'a
wówczas
| | c | | c | |
x1*x2=√ |
| , gdzie |
| >0 |
| | a | | a | |
2 sie 20:46
Saizou : a do drugiego może jakaś podpowiedź

2 sie 21:05
Eta:
Hej
Saizou 
Odpuść sobie zad.2 rozwiążesz go jak przerobisz ciągi

2 sie 21:40
Eta:
Zaraz Ci napiszę parę innych zadań

chcesz?
2 sie 21:41
Saizou : Witam Panią

oczywiście
Eto
2 sie 21:48
Eta:
zad 1/ Wykaż,że ostatnią cyfrą liczby 4
760+2
2012 jest
0
zad2/W trapezie ABCD , gdzie podstawy a= |AB| , b= |CD| i wysokość h= |DF|
przedłużono ramiona, które przecięły się w punkcie
E
Wyznacz pole trójkąta DEC
zad3/ Dany jest trapez ABCD ( AB II CD).
Wiedząc,że |AD|= |DC| i |AC|= BC| i |AD|= |DC|+|BC|
Wyznacz miary kątów tego trapezu
zad 4/ W trójkącie równoramiennym o podstawie
a i ramionach
b
Kąt między ramionami ma miarę
20o
Wykaż, że długości boków spełniają równość a
3+b
3= 3ab
2
Powodzenia

2 sie 21:57
rumpek: 
2 sie 22:00
Eta:
O co biega? ....
rumpek 
2 sie 22:02
rumpek: aaa nic

2 sie 22:07
2 sie 22:09
2 sie 22:10
Eta:
2/ gitara

2 sie 22:12
nikt : Nawet kartki nie musiałem wyjąć

Rzeczywiście proste zadanie

2 sie 22:13
Saizou : a ja siedzę nadal nad pierwszym i dochodzę do momentu
21520+22012=21520(1+2492)
2 sie 22:17
Eta:
Kurczę tam ma być [C [8]]
670 ( sorry

2 sie 22:18
Eta:
8670
2 sie 22:19
nikt : 
2 sie 22:20
Eta:


2 sie 22:21
Saizou : to tera to robi się proste:
8670+22012=22010+22012=22010(1+22)=22010*5
22010 jest zawsze parzyste, a iloczyn liczby parzystej z liczbą 5 ma zawsze na miejscu
jedności 0
cnu
2 sie 22:22
Eta:

2 sie 22:24
Eta:
Krótko mówiąc i elegancko

Taka liczba jest podzielna przez
10
2 sie 22:25
Eta:
@
nikt możesz dawać zad,4/

2 sie 22:29
nikt : mogę zrobić ?
2 sie 22:30
Eta: Możesz

2 sie 22:35
nikt : Próbuję

2 sie 22:37
Eta:
Słone? czy słodkie? ....

2 sie 22:37
nikt : Nie mam żadnego punktu zaczepienia

Czekam na
Saizou
2 sie 22:44
Eta:


2 sie 22:45
Eta:
To wbij haczyk w ścianę

2 sie 22:45
Saizou : jestem na razie na drugim, ale gdzieś błąd popełniłem i go szukam
2 sie 22:46
Saizou : wnerwiłem się i nie rysuję, bo coś idzie nie tak

| ax | | (a+b)h | | (x−h)b | |
| = |
| + |
|
|
| 2 | | 2 | | 2 | |
| | | | bh2 | |
zatem PCDE= |
| = |
| |
| | 2 | | 2(a−b) | |
2 sie 22:54
Saizou : z zadanie 3 jest coś nie tak bo
Wiedząc,że |AD|= |DC| i |AC|= BC| i |AD|= |DC|+|BC| jest nie do wykonania
2 sie 22:57
Eta:
Ech

chochlik
|AB| = |DC|+|BC|
2 sie 23:00
nikt : Chyba zrobiłem 4 xD
2 sie 23:02
nikt : Mam wrzucać to "coś" ?
2 sie 23:02
Eta:
Możesz, bo
Saizou jest dopiero w 1 LO

2 sie 23:05
Saizou : dajcie mi szanse

2 sie 23:06
nikt : ale tylko proszę mnie nie wyśmiać

Rysunek chyba jest zbędny

2 sie 23:06
nikt : 
2 sie 23:06
Eta:
Ok.........
nikt poczekaj na
Saizou 
2 sie 23:07
nikt : ale moje rozwiązanie jest strasznie naciągane

2 sie 23:10
Saizou : to zajmę się 4 a trzecie zrobię później
2 sie 23:11
Eta:
Nie ma rozwiązań "naciąganych" !


2 sie 23:12
nikt : Cholercia

Nie mam rozwiązania

Za to policzyłem wartość sin10
o 
2 sie 23:21
Eta:

2 sie 23:23
Saizou : ja próbowałem przyrównać pola
2 sie 23:25
nikt : MAM

Teraz to już nawet nie jest naciągany

Nie potrzebnie liczyłem wzorami Cardano

2 sie 23:25
Eta:

2 sie 23:26
nikt : Ja idę na jakieś 30 min z forum

2 sie 23:29
Saizou : poddaje się, nie mam pomysłu co do zadanie 4
2 sie 23:36
nikt : pisać czwarte czy jeszcze chcesz popróbować?
2 sie 23:54
Saizou : nie ja się poddaje
2 sie 23:57
Eta:
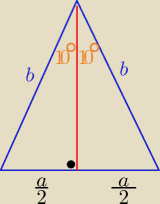 1 sposób
1 sposób
| | a | | 1 | |
sin10o= |
| |
| = sin30o= sin(3*10o) |
| | 2b | | 2 | |
korzystam ze wzoru
sin3α= 3sinα− 4sin3α
| | 1 | | a | | a3 | |
zatem : |
| = 3* |
| −4* |
| /* 2b3 |
| | 2 | | 2b | | 8b3 | |
b
3= 3ab
2− a
3 ⇒ a
3+b
3=3ab
2
c.n.u
Miłych snów


2 sie 23:58
Saizou : Miłych snów Eto
2 sie 23:59
nikt : Ja zrobiłem tak :
a
3 + b
3 = 3ab
2 inaczej :
a
3 − 3ab
2 + b
3 = 0
| | b | | b | |
1 − 3( |
| )2 + ( |
| )3 = 0 |
| | a | | a | |
Teraz przejdźmy do dowodu. Zauważmy że z twierdzenia sinusów mamy że :
| b | | sin80o | | 2 * sin10o * cos10o | |
| = |
| = |
| = |
| a | | sin20o | | 2 * sin10o * sin20o | |
zatem wystarczy wykazać że :
| | 1 | | 1 | |
1 − 3*( |
| )2 + ( |
| )3 = 0 |
| | 2sin10o | | 2sin10o | |
Istotnie :
| | 6 | | 1 | |
1 − |
| + |
| = 0 |
| | 8sin210o | | 8sin310o | |
8sin
3 10
o − 6sin10
o + 1 = 0
teraz korzystamy ze wzoru na sinus kąta potrójnego :
sin3x = 3sinx − 4sin
3x
i mamy że :
−2(−4sin
3 10
o + 3sin10
o) + 1 = 0
−2 * sin30
o + 1 = 0
−1 + 1 = 0
0 = 0
c.k.d.
3 sie 00:02
Eta:

3 sie 00:04
nikt : ale mogę tak o sobie przekształcać to co mam udowodnić ?
3 sie 00:05
rumpek: jeżeli dochodzisz do prawdy do tak (w tym przypadku 0 = 0) L = P, lecz są przypadki, gdy jest
to zabronione

ale tu wygląda

3 sie 00:06
rumpek: do = to*
3 sie 00:06
Eta:

3 sie 00:07
Vax: Po prostu jeżeli przekształcasz równoważnie to możesz.
3 sie 00:07
nikt : Bardzo interesujące zadanko moim zdaniem

Takie nietypowe

3 sie 00:11
Vax: Jak ktoś chce, to mam pod ręką takie fajne zadanko:
Wykaż, że jeżeli dla pewnych ustalonych a,b,c ∊ ℛ zachodzi:
|ax+by+cz| + |bx+cy+az| + |cx+ay+bz| = |x|+|y|+|z|
Dla dowolnych x,y,z ∊ ℛ, to dwie spośród a,b,c są równe 0, a trzecia jest równa ± 1.
3 sie 00:18
AS:
1. Wykazać,że jeśli a,b,c są miarami boków trójkąta prostokątnego
o przeciwprostokątnej c, to równanie x2 − 2*(a2 + b2)*x + c4 = 0 ma
tylko jeden pierwiastek podwójny.
2. Wykazać,że jeżeli a,b,c są miarami boków trójkąta rozwartokątnego
w którym c leży naprzeciw kąta rozwartego,to równanie
x2 − 2*c*x + a2 + b2 = 0 ma dwa pierwiastki dodatnie.
Zad. 1
Ponieważ z warunków zadania wiemy,że mowa jest o trójkącie prostokątnym
to a2 + b2 = c2 i nasze równanie ma postać
x2 − 2*c2*x + c4 = 0
Δ = 4*c4 − 4*c4 = 0
Wniosek: istnieje jeden pierwiastek podwójny
Uwaga: w temacie pierwotnym zabrakło x − pardon.
Zad. 2
Δ = 4*c2 − 4*(a2 + b2) = 4*(c2 − (a2 + b2)) > 0
gdyż c2 > a2 + b2
3 sie 09:51
AS:
1. Wykreślić konstrukcyjnie trzy okręgi wzajemnie styczne
znając położenie ich środków .(tzn.znane są ich odległości p,q,r)
2. Dowieść,że jeżeli
| | (p − b)*(p − c) | | (p − c)*(p − a) | |
x2 = |
| , y2 = |
| |
| | p*(p − a) | | p*(p − b) | |
| | (p − a)*(p − b) | |
z2 = |
| |
| | p*(p − c) | |
gdzie 2p = a + b + c
to x*y + y*z + z*x = 1
| | n4 | | n3 | | n2 | |
3. Wykaż,że wyrażenie |
| + |
| + |
| |
| | 4 | | 2 | | 4 | |
jest dla każdego całkowitego n kwadratem liczby całkowitej.
3 sie 09:59
Kejt: sępię się na te zadanka.. mogę się jakimś poczęstować?
3 sie 12:10
Eta:
zad3/ jest banalne

Dawaj
Kejt ten dowód

3 sie 13:47
Mila: Kejt, chyba na obiedzie.
Eto, gdzie nasza Basia, czy wiosłuje w Londynie?
3 sie 16:37
Godzio: Vax, coś w tę stronę

?
|ax+by+cz| + |bx+cy+az| + |cx+ay+bz| = |x|+|y|+|z|
|ax+by+cz| + |bx+cy+az| + |cx+ay+bz| ≤
|ax| + |by| + |cz| + |bx| + |cy| + |az| + |cx| + |ay|+ |bz| =
= (|a| + |b| + |c|)(|x| + |y| + |z|), zatem:
|x|+|y|+|z| ≤ (|a| + |b| + |c|)(|x| + |y| + |z|) ⇒ |a| + |b| + |c| ≥ 1
3 sie 22:22
lisa: Vax : Jest tylko jeden mały problem (nie żebym się czepiała) : jeżeli x=y=z, to a=b=c= 1/3 też
spełniają warunki zadania. To byłby kontrprzykład.
3 sie 23:00
Vax: | | 1 | |
Ale to ma zachodzić dla wszystkich rzeczywistych x, dla a=b=c= |
| łatwo podać taką |
| | 3 | |
trójkę (x,y,z), że to nie zachodzi

4 sie 00:03
Vax: rzeczywistych x,y,z*
4 sie 00:05
Vax: rzeczywistych x,y,z*
4 sie 00:06
Vax: Godzio, raczej radziłbym w tym zadaniu posprawdzać co się dzieje dla jakichś szczególnych
trójek (x,y,z), np dla x=y=z, albo x=y=0 itd

Jbc jutro po południu postaram się wrzucić
dowód tego.
4 sie 00:11
Godzio:
No to nie mam pomysłu

Takie wstawianie ? Dziwne, no nic, ja lecę spać

4 sie 00:14
lisa: Ok, rzeczywiście "dla dowolnych" ...(chyba za dużo zadanek na dziś rozwiązałam i już nie
rozumiem co czytam) No cóż

Nie wrzucaj jeszcze tego dowodu, to pobawię się tym trochę
jutro.
4 sie 00:26
AS:
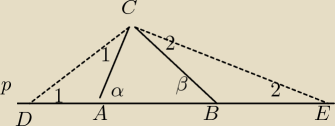
Widzę,że zadania konstrukcyjne nie cieszą się powodzeniem.
A szkoda.Każde z nich wymaga odrębnego podejścia.
Podaję szkic rozwiązania
Zadanie 1
Zbudować konstrukcyjnie trójkąt, mając dane jego obwód i dwa kąty wewnętrzne.
Zacząć trzeba od analizy zadania
Niech ΔABC będzie tym poszukiwanym.
Na prostej p odkładam odcinki AD = AC , BE = BC.
Wtedy odcinek DE jest obwodem naszego trójkąta.
Trójkąty DAC i BEC są równoramienne mające po dwa kąty równe
<1 + <1 + 180 − α = 180 => <1 = α/2
<2 + <2 + 180 − β = 180 => <2 = β/2
Rozwiązanie
1. Na prostej p odkładam odcinek DE = obwodowi trójkąta.
2. Wykonuję konstrukcje podziału kątów α i β na połowy.
3. Przy punkcie D odkładam kąt 1 = α/2 a przy punkcie E kąt 2 = β/2
4. Przedłużenia ramion tych kątów wyznaczą punkt C
5. Przy boku DC odkładam kąt α/2 , jego ramię wyznaczy punkt A
6. Przy boku CE odkładam kąt β/2 , jego ramię wyznaczy punkt B
W ten sposób wyznaczyłem szukany trójkat.Są 4 rozwiązania
Zadanie 2
Wykreślić konstrukcyjnie trzy okręgi wzajemnie styczne znając położenie ich środków .
(tzn.znane są ich odległości p,q,r)
Oznaczając szukane okręgi przez O1(A,r1) , O2(B,r2) , O3(C,r3) mamy
r1 + r2 = p , r2 + r3 = q , r1 + r3 = r
Rozwiązując ten układ równań,znajdziemy
r1 = 1/2(p + r − q) , r2 = 1/2(p + q − r) , r3 = 1/2(q + r − p)
Wystarczy teraz na prostej odłożyć kolejno odcinki p i r , umniejszyć o q
i wziąć połowę tego odcinka,by otrzymać r1
Analogicznie znajdziemy promienie r2 i r3
4 sie 09:50
Eta:
@
Saizou 
Czekam na rozwiązanie zad.3/ ......... z kątami trapezu

4 sie 21:44
Saizou : całkowicie o nim zapomniałem
Eto 
4 sie 21:46
Saizou :
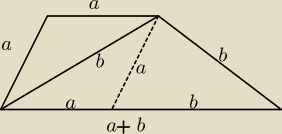
na razie mam rysunek

4 sie 21:49
Eta:
I pięknie

4 sie 21:54
Saizou :
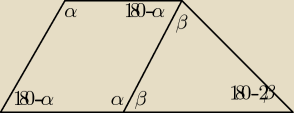
β=180−α
180−2(180−α)=180−360+2α=−180+2α
180−α+180−α=360−2α
4 sie 22:11
Eta:
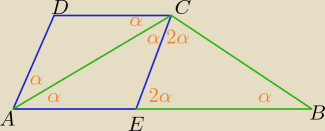
A teraz ? .........

4 sie 22:17
Saizou : α=36
4α=144
2α=72
∠D =180−72=108
4 sie 22:19
Eta:
No wreszcie! ......


4 sie 22:19
Eta:
zad4/ Wiedząc,że a, b>0 i a
2+b
2= 6ab
wyznacz wartość:
4 sie 22:21
Saizou : bo ubzdurałem sobie że kąt alfa powinien być tam gdzie go zaznaczyłem

4 sie 22:22
Eta:

4 sie 22:23
Saizou : teraz jestem trochę zajęty ale jak znajdę czas to to postaram się zrobić
4 sie 22:26
Saizou : a
2+b
2=6ab
(a−b)
2=
√4ab
la−bl=2
√ab tu mam pytanie, trzeba rozpatrzeć 2 przypadki

(a+b)
2=8ab
la+bl=
√8ab
a+b=
√8ab
4 sie 23:06
Saizou : dla la−bl nieujemnego:
dla la−bl ujemnego:
4 sie 23:15
rumpek: Saizou 151917 zostawiłem tu dla Ciebie dowodzik

tam z tym trójkątem (koniec
postów)
4 sie 23:25
Saizou : a prosta k przechodzi przez środek boku

4 sie 23:31
rumpek: nie

4 sie 23:34
Saizou : czyli inaczej mówiąc mam wykazać, że AE=DC, bo z tego wyniknie że AD+AE=CD
4 sie 23:41
rumpek: nie utrudniaj sobie

4 sie 23:48
Godzio: To ja dodam zadanie. Może się przebije w tym natłoku
 Zad. 1
Zad. 1
Wyznacz długości boków a,b,c trójkąta mająca dane środkowe: s
1,s
2,s
3.
4 sie 23:50
Saizou :
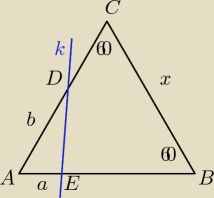
Korzystając z rysunku i własności podanych na nim, wykaż, że a + b = x, czyli:
|BC| = |AC| = |AB| = |AE| + |AD|
4 sie 23:53
Saizou : Godzio niestety ale musisz poczekać, bo jeszcze zadanie od Mili muszę zrobić
4 sie 23:53
Godzio:
Wiem wiem

Ja dopiero będę w poniedziałek wieczorem. Do tego czasu chyba już będzie.
4 sie 23:54
Saizou : ja idę spać bo dzisiaj to już nic nie wymyślę
Miłej nocy wszystkim

5 sie 00:05
Eta:
Dobranoc


5 sie 00:23
5 sie 00:29
Saizou : jakaś podpowiedź do trójkąta

5 sie 12:13





 wszystkich sześcianów jednostkowych jest
v=10*10*10=1000
zauważmy, że dwie ściany pomalowane będzie miał sześcian który jest stworzony ze styku ścian:
zatem
−na przedniej ścianie jest ich:32
− na ścianie z tyłu : 32
− na prawej 16
− na lewej 16
−na górnej 0
na dolnej 0 , wówczas sześcianów pomalowanych na dwóch stron jest 96
pomalowanych z jednej strony będzie:
8*8*6=384
a pomalowanych z trzech stron będzie 8
wszystkich sześcianów jednostkowych jest
v=10*10*10=1000
zauważmy, że dwie ściany pomalowane będzie miał sześcian który jest stworzony ze styku ścian:
zatem
−na przedniej ścianie jest ich:32
− na ścianie z tyłu : 32
− na prawej 16
− na lewej 16
−na górnej 0
na dolnej 0 , wówczas sześcianów pomalowanych na dwóch stron jest 96
pomalowanych z jednej strony będzie:
8*8*6=384
a pomalowanych z trzech stron będzie 8
 zadanie było proste jak ktoś ma dobre wyobrażenie przestrzenne
zadanie było proste jak ktoś ma dobre wyobrażenie przestrzenne



 Odpuść sobie zad.2 rozwiążesz go jak przerobisz ciągi
Odpuść sobie zad.2 rozwiążesz go jak przerobisz ciągi 
 chcesz?
chcesz?
 oczywiście Eto
oczywiście Eto








 Rzeczywiście proste zadanie
Rzeczywiście proste zadanie 





 Taka liczba jest podzielna przez 10
Taka liczba jest podzielna przez 10




 Czekam na Saizou
Czekam na Saizou




 chochlik |AB| = |DC|+|BC|
chochlik |AB| = |DC|+|BC|


 Rysunek chyba jest zbędny
Rysunek chyba jest zbędny 





 Nie mam rozwiązania
Nie mam rozwiązania  Za to policzyłem wartość sin10o
Za to policzyłem wartość sin10o 

 Teraz to już nawet nie jest naciągany
Teraz to już nawet nie jest naciągany  Nie potrzebnie liczyłem wzorami Cardano
Nie potrzebnie liczyłem wzorami Cardano 


 1 sposób
1 sposób



 ale tu wygląda
ale tu wygląda 

 Takie nietypowe
Takie nietypowe 
 Dawaj Kejt ten dowód
Dawaj Kejt ten dowód 
 ?
|ax+by+cz| + |bx+cy+az| + |cx+ay+bz| = |x|+|y|+|z|
|ax+by+cz| + |bx+cy+az| + |cx+ay+bz| ≤
|ax| + |by| + |cz| + |bx| + |cy| + |az| + |cx| + |ay|+ |bz| =
= (|a| + |b| + |c|)(|x| + |y| + |z|), zatem:
|x|+|y|+|z| ≤ (|a| + |b| + |c|)(|x| + |y| + |z|) ⇒ |a| + |b| + |c| ≥ 1
?
|ax+by+cz| + |bx+cy+az| + |cx+ay+bz| = |x|+|y|+|z|
|ax+by+cz| + |bx+cy+az| + |cx+ay+bz| ≤
|ax| + |by| + |cz| + |bx| + |cy| + |az| + |cx| + |ay|+ |bz| =
= (|a| + |b| + |c|)(|x| + |y| + |z|), zatem:
|x|+|y|+|z| ≤ (|a| + |b| + |c|)(|x| + |y| + |z|) ⇒ |a| + |b| + |c| ≥ 1

 Jbc jutro po południu postaram się wrzucić
dowód tego.
Jbc jutro po południu postaram się wrzucić
dowód tego.
 Takie wstawianie ? Dziwne, no nic, ja lecę spać
Takie wstawianie ? Dziwne, no nic, ja lecę spać 
 Nie wrzucaj jeszcze tego dowodu, to pobawię się tym trochę
jutro.
Nie wrzucaj jeszcze tego dowodu, to pobawię się tym trochę
jutro.
 Widzę,że zadania konstrukcyjne nie cieszą się powodzeniem.
A szkoda.Każde z nich wymaga odrębnego podejścia.
Podaję szkic rozwiązania
Zadanie 1
Zbudować konstrukcyjnie trójkąt, mając dane jego obwód i dwa kąty wewnętrzne.
Zacząć trzeba od analizy zadania
Niech ΔABC będzie tym poszukiwanym.
Na prostej p odkładam odcinki AD = AC , BE = BC.
Wtedy odcinek DE jest obwodem naszego trójkąta.
Trójkąty DAC i BEC są równoramienne mające po dwa kąty równe
<1 + <1 + 180 − α = 180 => <1 = α/2
<2 + <2 + 180 − β = 180 => <2 = β/2
Rozwiązanie
1. Na prostej p odkładam odcinek DE = obwodowi trójkąta.
2. Wykonuję konstrukcje podziału kątów α i β na połowy.
3. Przy punkcie D odkładam kąt 1 = α/2 a przy punkcie E kąt 2 = β/2
4. Przedłużenia ramion tych kątów wyznaczą punkt C
5. Przy boku DC odkładam kąt α/2 , jego ramię wyznaczy punkt A
6. Przy boku CE odkładam kąt β/2 , jego ramię wyznaczy punkt B
W ten sposób wyznaczyłem szukany trójkat.Są 4 rozwiązania
Zadanie 2
Wykreślić konstrukcyjnie trzy okręgi wzajemnie styczne znając położenie ich środków .
(tzn.znane są ich odległości p,q,r)
Oznaczając szukane okręgi przez O1(A,r1) , O2(B,r2) , O3(C,r3) mamy
r1 + r2 = p , r2 + r3 = q , r1 + r3 = r
Rozwiązując ten układ równań,znajdziemy
r1 = 1/2(p + r − q) , r2 = 1/2(p + q − r) , r3 = 1/2(q + r − p)
Wystarczy teraz na prostej odłożyć kolejno odcinki p i r , umniejszyć o q
i wziąć połowę tego odcinka,by otrzymać r1
Analogicznie znajdziemy promienie r2 i r3
Widzę,że zadania konstrukcyjne nie cieszą się powodzeniem.
A szkoda.Każde z nich wymaga odrębnego podejścia.
Podaję szkic rozwiązania
Zadanie 1
Zbudować konstrukcyjnie trójkąt, mając dane jego obwód i dwa kąty wewnętrzne.
Zacząć trzeba od analizy zadania
Niech ΔABC będzie tym poszukiwanym.
Na prostej p odkładam odcinki AD = AC , BE = BC.
Wtedy odcinek DE jest obwodem naszego trójkąta.
Trójkąty DAC i BEC są równoramienne mające po dwa kąty równe
<1 + <1 + 180 − α = 180 => <1 = α/2
<2 + <2 + 180 − β = 180 => <2 = β/2
Rozwiązanie
1. Na prostej p odkładam odcinek DE = obwodowi trójkąta.
2. Wykonuję konstrukcje podziału kątów α i β na połowy.
3. Przy punkcie D odkładam kąt 1 = α/2 a przy punkcie E kąt 2 = β/2
4. Przedłużenia ramion tych kątów wyznaczą punkt C
5. Przy boku DC odkładam kąt α/2 , jego ramię wyznaczy punkt A
6. Przy boku CE odkładam kąt β/2 , jego ramię wyznaczy punkt B
W ten sposób wyznaczyłem szukany trójkat.Są 4 rozwiązania
Zadanie 2
Wykreślić konstrukcyjnie trzy okręgi wzajemnie styczne znając położenie ich środków .
(tzn.znane są ich odległości p,q,r)
Oznaczając szukane okręgi przez O1(A,r1) , O2(B,r2) , O3(C,r3) mamy
r1 + r2 = p , r2 + r3 = q , r1 + r3 = r
Rozwiązując ten układ równań,znajdziemy
r1 = 1/2(p + r − q) , r2 = 1/2(p + q − r) , r3 = 1/2(q + r − p)
Wystarczy teraz na prostej odłożyć kolejno odcinki p i r , umniejszyć o q
i wziąć połowę tego odcinka,by otrzymać r1
Analogicznie znajdziemy promienie r2 i r3
 Czekam na rozwiązanie zad.3/ ......... z kątami trapezu
Czekam na rozwiązanie zad.3/ ......... z kątami trapezu 

 na razie mam rysunek
na razie mam rysunek 

 β=180−α
180−2(180−α)=180−360+2α=−180+2α
180−α+180−α=360−2α
β=180−α
180−2(180−α)=180−360+2α=−180+2α
180−α+180−α=360−2α
 A teraz ? .........
A teraz ? ......... 




 (a+b)2=8ab
la+bl=√8ab
a+b=√8ab
(a+b)2=8ab
la+bl=√8ab
a+b=√8ab



 Zad. 1
Wyznacz długości boków a,b,c trójkąta mająca dane środkowe: s1,s2,s3.
Zad. 1
Wyznacz długości boków a,b,c trójkąta mająca dane środkowe: s1,s2,s3.
 Korzystając z rysunku i własności podanych na nim, wykaż, że a + b = x, czyli:
|BC| = |AC| = |AB| = |AE| + |AD|
Korzystając z rysunku i własności podanych na nim, wykaż, że a + b = x, czyli:
|BC| = |AC| = |AB| = |AE| + |AD|
 Ja dopiero będę w poniedziałek wieczorem. Do tego czasu chyba już będzie.
Ja dopiero będę w poniedziałek wieczorem. Do tego czasu chyba już będzie.








