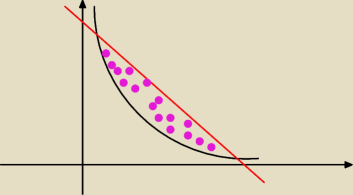
skorygujcie prosze vcx: Pole obszaru ograniczone y=⁶_x i y=5−x to całka podwójna taka: _⁶x∫^5−x ₋₁∫⁰ (5−x)− ⁶_x dx dy

Basia: dlaczego podwójna ? przecież masz dwie funkcje jednej zmiennej i wszystko dzieje się na płaszczyźnie znajdź punkty wspólne hiperboli i prostej i będzie całka _a∫^b [ 5−x − ⁶_x ] dx

Basia: ⁶_x = 5−x /*x 6 = 5x − x² x² − 5x + 6 = 0 Δ=1 x₁ = 2 x₂ = 3 a = 2 b=3 i tyle

vcx: aaa bo ja żle narysowałam sobie wykres na kartce i zrobiłam taki głupi błąd, że az wstyd się przyznac Basiu. Dziękuje bardzo za pomoc i mam pytanie, dlaczego nie całka podwójna? Wiem, napisałaś, że " dwie funkcje jednej zmiennej i wszystko dzieje się na płaszczyźnie", czyli gdybym miałam jeszcze np jedną zmienną i pole występowało by w trójwymiarze to dopiero była by całka podwójna? Albo jak wygląda przykładowe zadanie z całką podwójną tzn jak np wygląda zapis obszaru (np. 1<x<2 i <4<y<4 i tu liczymy podwójną)? Szukam i nie mogę nigdzie trafić. A punty a i b to są punkty tak, że a ogranicza a więc ta mniejsza wartosc z osi y, b ta wyższa? I jakie przykładowe funkcje moga być podane które ograniczają obszar i mamy go obliczyć? Mogłabyś coś dla mnie wymyślić, bardzo prosze, bo chcialabym poćwiczyć z podówjnymi

Basia: poszukaj na tej stronie; było ostatnio sporo zadań

Basia: tu coś jest i chyba bardzo proste, a nie jest rozwiązane https://matematykaszkolna.pl/forum/151158.html wrzuć do wyszukiwarki "szukaj na forum" (na górze strony) słowa "całka podwójna" sporo znajdziesz

Basia: całka podwójna to całka z jakiejś funkcji (na ogół dwóch zmiennych) liczona po obszarze, który jest jakąś częścią płaszczyzny (najczęściej XOY) np. po kole, albo po trójkącie, albo po prostokącie (wtedy łatwiutko) wymyślać od ręki nie będę, bo coś pozornie prostego może się okazać koszmarne dlatego doradzam przeszukanie forum całka potrójna to całka z jakiejś funkcji (na ogół trzech zmiennych) liczona po jakimś fragmencie przestrzeni trójwymiarowej np. po kuli

Krzysiek: ∫∫_D dxdy to wtedy liczysz pole obszaru D gdy: D={(x,y) , x∊[a,b],y∊[c,d]} to wtedy ∫∫_D dxdy to pole prostokąta o boku 'b−a' i 'd−c' ∫_a^b f(x)dx − to jest to pole pod wykresem funkcji f(x) ograniczone funkcją y=0 dla x∊[a,b] więc tak naprawdę jak liczymy pole to liczymy całkę podwójną:

	6
∫ab [5−x−		]dx =∫ab (∫5−x6/x dy )dx
	x