Środkowe trójkąta. Dowód...
V.Abel: Udowodnij, że jeśli środkowe trójkąta przecinają się w jednym punkcie, to ich środkowe dzielą
się w stosunku 2:1.
Proszę o pomoc....
19 cze 23:19
Mila:
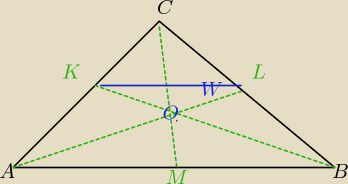
K, L,M środki boków Δ.
Odcinek KL jest równoległy AB na podstawie tw. odwrotnego do twierdzenia Talesa i
W takim razie czworokąt ABLK jest trapezem.
ΔKLO jest podobny doΔABO w skali 1:2.
|LO| : |AO|=1 : 2
|KO| : OB|=1 : 2
analogicznie można wykazać, że |OM| : |OC|=1:2
c.n.w
jest wiele dowodów , najczęsciej podawany jest w wersji wektorowej.
20 cze 00:23
Mila:
Zadanie źle sformułowane.
Środkowa trójkąta to prosta zawierająca wierzchołek trójkąta i środek przeciwległego boku.
Każdy trójkąt ma trzy środkowe, które przecinają się w jednym punkcie, będącym środkiem
ciężkości (środkiem masy, barycentrum) trójkąta
Punkt ten dzieli każdą ze środkowych na dwie części, przy czym odcinek łączący barycentrum z
wierzchołkiem jest dwa razy dłuższy od odcinka łączącego barycentrum ze środkiem boku.
20 cze 15:04
Mila: Definicja środkowej, zobacz wikipedia.
20 cze 16:14
V.Abel: Znam definicję środkowej, dzięki Mila

A wiesz może jak to zrobić na zasadzie podobieństwa pól trójkątów ? . .
20 cze 21:54
b.: zadanie jest dobrze (choc dziwnie) sformulowane
20 cze 22:04
V.Abel: Za treść nie odpowiadam, bo nie ja układałem zadanie

A mogłabyś napisać też wektorową wersję, ja wiem, że mógłbym sobie go poszukać, ale liczę na
rzetelne i (w ogóle jakieś

) tłumaczenie

. Naprawdę bardzo proszę . . .
20 cze 22:04
20 cze 22:14
Mila:
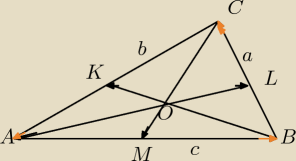
suma wektorów dla ΔABC
c
→+a
→+b
→=0
środkowe
b
→=−c
→−a
→
Pomijam strzałki przy nazwie wektorów.
W ΔABO:
c=k*S
a−m*S
b k, m liczby , a,c ,S
a,S
b to wektory
| | 1 | | 1 | |
c=k(c+1/2a)−m( |
| a− |
| c) |
| | 2 | | 2 | |
c= kc+0,5 ka−0,5ma+0,5 mc
c=(k*c+0,5m*c)+(0,5k*a−0,5m*a)
c
→=(k+0,5m)*c
→+(0,5k−0,5m)*a
równość będzie prawdziwa, gdy
k+0,5m=1
i 0,5k−0,5m=0
z drugiego k=m
k+0,5k=1
wykazaliśmy, że c
→=k*S
a→−m*S
b→ =
| | 2 | | 1 | |
czyli AO = |
| Sa stąd OL= |
| Sa |
| | 3 | | 3 | |
| | 2 | | 1 | |
OB= |
| Sb i OK= |
| S</div> |
| | 3 | | 3 | |
Srodkowe dzielą się w stosunku 2:1.
21 cze 00:16
Mila: Vax na pewno zna kilka wersji dowodu, może dołączy?
21 cze 10:07
V.Abel: Ok, dzięki za pomoc

21 cze 21:26
Mila: 
powodzenia na lekcjach.
21 cze 22:22
Maitner: Mam nadzieję, że nie będzie to dla Ciebie w żaden sposób obraźliwe, ale czy mógłbym prosić o
trzymanie się jednej konwencji w rozwiązaniu? W sensie np. używanie ułamków zwykłych i
dziesiętnych.
4 mar 21:23
5-latek : Alez gościu bez jaj
czy dla ucznia szkoły sredniej stanowi to az tak wielki problem (zamiana ułamka dziesiętnego
na zwykly ?
jeśli tak to wroc do podstawówki
4 mar 21:28
Mila:
Tak, zapamiętam.
4 mar 22:18
PW: Ale się tu dziwacy kręcą − do zadania sprzed 4 lat takie subtelne uwagi ... Malejemy do szeptu.
4 mar 23:47
Mila:
Zauważyłam od pewnego czasu , że pojawiają się w stosunku do mnie różne dziwne uwagi.
Trzeba zniknąć z forum.

4 mar 23:52
 K, L,M środki boków Δ.
Odcinek KL jest równoległy AB na podstawie tw. odwrotnego do twierdzenia Talesa i
K, L,M środki boków Δ.
Odcinek KL jest równoległy AB na podstawie tw. odwrotnego do twierdzenia Talesa i
 A wiesz może jak to zrobić na zasadzie podobieństwa pól trójkątów ? . .
A wiesz może jak to zrobić na zasadzie podobieństwa pól trójkątów ? . .
 A mogłabyś napisać też wektorową wersję, ja wiem, że mógłbym sobie go poszukać, ale liczę na
rzetelne i (w ogóle jakieś
A mogłabyś napisać też wektorową wersję, ja wiem, że mógłbym sobie go poszukać, ale liczę na
rzetelne i (w ogóle jakieś  ) tłumaczenie
) tłumaczenie  . Naprawdę bardzo proszę . . .
. Naprawdę bardzo proszę . . .
 suma wektorów dla ΔABC
c→+a→+b→=0
środkowe
suma wektorów dla ΔABC
c→+a→+b→=0
środkowe

 powodzenia na lekcjach.
powodzenia na lekcjach.
