Zadania maturalne
Bogdan:
Zadania maturalne.
| | 1 | | 4 | | 8 | |
1. Rozwiązać równanie: x3 + 4x2 + 8x + |
| + |
| + |
| = 70 |
| | x3 | | x2 | | x | |
2. Wyrazy ciągu (a
n) spełniają warunki: a
1 = 1 i a
n+1 = 2a
n + 1. Obliczyć a
2010
3. Wyznaczyć współrzędne środka ciężkości trójkąta ABC, dla A = (x
1, y
1), B = (x
2, y
2),
C = (x
3, y
3)

14 sie 17:43
AS:
Zad.1
| | 1 | | 1 | | 1 | |
x3 + |
| + 4*(x2 + |
| ) + 8*(x + |
| ) = 70 |
| | x3 | | x2 | | x | |
Podstawiam
| | 1 | | 1 | | 1 | |
(x + |
| )2 = x2 + 2 + |
| → x2 + |
| = u2 − 2 |
| | x | | x2 | | x2 | |
| | 1 | | 1 | | 1 | |
x3 + |
| = (x + |
| )*(x2 − 1 + |
| ) = u*(u2 − 3) |
| | x3 | | x | | x2 | |
Stąd równanie
u
3 − 3*u + 4*u
2 − 8 + 8*u = 70
u
3 + 4*u
2 + 5*u − 78 = 0
Równanie to ma jedyny pierwiastek rzeczywisty u = 3
| | 1 | |
Teraz wystarczy rowziązać równanie x + |
| = 3 |
| | x | |
14 sie 19:15
Godzio:
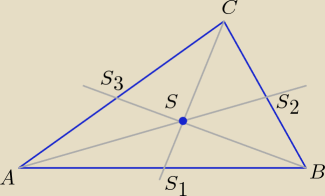
A(x
1,y
2)
B(x
2,y
3)
C(x
3,y
3)
| | x1 + x2 | | y1 + y2 | |
S1( |
| , |
| ) |
| | 2 | | 2 | |
| | x2 + x3 | | y2 + y3 | |
S2( |
| , |
| ) |
| | 2 | | 2 | |
| | x3 + x1 | | y3 + y1 | |
S3( |
| , |
| ) |
| | 2 | | 2 | |
prosta przechodząca przez S
1 i C :
| y1 + y2 | | x1 + x2 | |
| = a * |
| + b |
| 2 | | 2 | |
y
3 = ax
3 + b −
−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−
| y1 + y2 − 2y3 | | x1 + x2 − 2x3 | |
| = a( |
| |
| 2 | | 2 | |
| | y1 + y2 − 2y3 | |
a = |
| |
| | x1 + x2 − 2x3 | |
| | y1 + y2 − 2y3 | |
b = y3 − x3 * |
| |
| | x1 + x2 − 2x3 | |
| | y3x1 +y3x2 − 2x3y3 −y1x3 − y2 x3 + 2y3 x3 | |
b = |
| |
| | x1 + x2 − 2x3 | |
| | y3x1 + y3x2 − y1x3 − y2x3 | |
b = |
| |
| | x1 + x2 − 2x3 | |
| | y1 + y2 − 2y3 | |
y = |
| * x + |
| | x1 + x2 − 2x3 | |
| y3x1 + y3x2 − y1x3 − y2x3 | |
| |
| x1 + x2 − 2x3 | |
prosta AS
2 :
| y2 + y3 | | x2 + x3 | |
| = a * |
| + b |
| 2 | | 2 | |
y
1 = ax
1 + b −
−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−
| | y2 + y3 − 2y1 | |
a = |
| |
| | x2 + x3 − 2x1 | |
| | x2y1 + x3y1 − 2x1y1 − y2x1 − y3x1 − 2x1y1 | |
b = |
| |
| | x2 + x3 − 2x1 | |
| | x2y1 + x3y1 − y2x1 − y3x1 | |
b = |
| |
| | x2 + x3 − 2x1 | |
| | y2 + y3 − 2y1 | |
y = |
| x + |
| | x2 + x3 − 2x1 | |
| | x2y1 + x3y1 − y2x1 − y3x1 | |
|
| |
| | x2 + x3 − 2x1 | |
Punkt przecięcia to tych prostych to S:
| y2 + y3 − 2y1 | |
| *x + |
| x2 + x3 − 2x1 | |
| | x2y1 + x3y1 − y2x1 − y3x1 | |
|
| = |
| | x2 + x3 − 2x1 | |
| | y1 + y2 − 2y3 | |
|
| * x + |
| | x1 + x2 − 2x3 | |
| y3x1 + y3x2 − y1x3 − y2x3 | |
| |
| x1 + x2 − 2x3 | |
| | y2 + y3 − 2y1 | | y1 + y2 − 2y3 | |
x( |
| − |
| ) = |
| | x2 + x3 − 2x1 | | x1 + x2 − 2x3 | |
| y3x1 + y3x2 − y1x3 − y2x3 | |
| − |
| x1 + x2 − 2x3 | |
| x2y1 + x3y1 − y2x1 − y3x1 | |
| |
| x2 + x3 − 2x1 | |
x((y
2+y
3−2y
1)(x
1+x
2−2x
3) − (y
1+y
2−2y
3)(x
2+x
3−2x
1))=
(y
3x
1+y
3x
2−y
1x
3−y
2x
3)(x
1+x
3−2x
1) −
(x
2y
1+x
3y
1−y
2x
1−y
3x
1)(x
1+x
2−2x
3)
x = ((y
3x
1+y
3x
2−y
1x
3−y
2x
3)(x
2+x
3−2x
1) −
(x
2y
1+x
3y
1−y
2x
1−y
3x
1)(x
1+x
2−2x
3)) /
( (y
2+y
3−2y
1)(x
1+x
2−2x
3) − (y
1+y
2−2y
3)(x
2+x
3−2x
1) )
−y
2x
2x
3+y
2x
2x
1−y
2x
32+y
2x
12+2y
3x
22−y
3x
2x
3+y
3x
3x
1−
2y
3x
12−y
1x
22−y
1x
2x
1+y
1x
32+y
1x
3x
1
/
y
2x
1 + x
2y
2 − 2x
3y
2+y
3x
1+y
3x
2−2x
3y
3− 2y
1x
1 − 2y
1x
2 + 4y
1x
3
− y
1x
2 − y
1x
3 + 2x
1y
1−y
2x
2−y
2x
3+2x
1y
2+2x
2y
3+2x
3y
3−4x
1y
3
y
2(−x
2x
3+x
2x
1−x
32+x
12)+y
3(x
22−x
2x
3+x
3x
1− x
12)+y
1(−x
22−x
2x
1+x
32+x
3x
1)
/
3y
2x
1 − 3x
3y
2−3y
3x
1+3y
3x
2 − 3y
1x
2 + 3y
1x
3
y
2(x
1−x
3)(x
1+x
2+x
3)−y
3(x
1−x
2)(x
1+x
2+x
3)−y
1(x
2−x
3)(x
2+x
3+x
1)
/
3y
2(x
1 − x
3) −3y
3(x
1−x
2) − 3y
1(x
2 − x
3)
| y2(x1−x3)−y3(x1−x2)−y1(x2−x3) | |
| |
| y2(x1 − x3) −y3(x1−x2) − y1(x2 − x3) | |
i wracając do podstawienia musi wyjść
Nic nie mówcie

14 sie 20:28
AS:
Środek ciężkości trójkąta leży na ptzecięciu się dwóch środkowych.
Ponadto punkt przecięcia się środkowych dzieli każdą z środkowych
na dwa odcinki w stosunku 2:1 (licząc od wierzchołka)
| | x1 + x2 | |
Środek odcinka AB(xs,ys) gdzie xs = |
| ,podobnie dla ys |
| | 2 | |
Podział odcinka w danym stosunku jak łatwo wykazać,wyrażą się wzorem
Dla k = 2 mamy
| | | | x1 + x2 + x3 | |
xk = |
| = |
| |
| | 1 + 2 | | 3 | |
Podobnie wyliczamy yk
14 sie 20:57
Kejt:
a1=1
a2=3
a3=7
a4=15
są to więc potęgi dwójki pomniejszone o 1.
an=2n−1
a2010=22010−1
dobrze?
14 sie 21:42
Bogdan:
 Zadanie 1 i 3
Zadanie 1 i 3.
As to as, od razu widać po sposobie rozwiązania
 Zadanie 3
Zadanie 3.
S = (a, b) to środek ciężkości trójkąta, czyli punkt przecięcia jego środkowych.
| | x1 + x2 | | y1 + y2 | |
D = ( |
| , |
| ) to środek boku AB |
| | 2 | | 2 | |
Zastosujemy wektory (pomijam znak → nad nazwą wektora).
| | x1 + x2 | | y1 + y2 | |
CS = [a − x3, b − y3], CD = [ |
| − x3, |
| − y3] |
| | 2 | | 2 | |
| | 2 | | x1 + x2 | | 2 | | y1 + y2 | |
⇒ [a − x3, b − y3] = [ |
| ( |
| − x3), |
| ( |
| − y3)] |
| | 3 | | 2 | | 3 | | 2 | |
| | 2 | | x1 + x2 | | x1 + x2 + x3 | |
a − x3 = |
| ( |
| − x3) ⇒ a = |
| |
| | 3 | | 2 | | 3 | |
| | 2 | | y1 + y2 | | y1 + y2 + y3 | |
b − y3 = |
| ( |
| − y3) ⇒ b = |
| |
| | 3 | | 2 | | 3 | |
14 sie 22:01
Bogdan:
Zadanie 2.
Dobrze
Kejt 
.
W bardziej rozbudowanym rozwiązaniu znalazłby się jeszcze dowód stwierdzenia:
"są to więc potęgi dwójki pomniejszone o 1", np. dowód indukcyjny.
14 sie 22:05
Kejt: mogę dołączyć ;>
a1=1
21−1=1
a2=3
22−1=3
a3=7
23−1=7
a4=15
24−1=15
tak wystarczy?
14 sie 22:07
Bogdan:
To nie jest dowód, to jest spostrzeżenie. Pokazałaś prawdziwość spostrzeżenia
dla n = 1, 2, 3 i 4 i nic więcej. Dowód powinien zawierać prawdziwość tezy dla
dowolnych wartości n.
14 sie 22:17
AS: Do Bogdana
Dziękuję za opinię,upadłem z zawrotu głowy.
Serdecznie pozdrawiam.
15 sie 07:59
Kejt: Bogdanie mógłbyś proszę napisać to bardziej rozbudowane rozwiązanie?
15 sie 12:34
Bogdan:
Zadanie 2. Wyrazy ciągu (an) spełniają warunki: a1 = 1 i an+1 = 2an + 1.
Obliczyć a2010
Ciąg (an) jest podany w postaci rekurencyjnej.
a1 = 1, a2 = 3, a3 = 7, a4 = 15, ...
Zauważam, że kolejne wyrazy ciągu powstają przez odjęcie jedynki od potęgi dwójki, czyli
an = 2n − 1 i n∊N+
Wykażę, że wzór ogólny ciągu (an): an = 2n − 1 jest prawdziwy dla każdej wartości n.
Stosuję indukcję matematyczną.
Krok 1. Sprawdzenie dla n = 1, 2, 3
Wzór rekurencyjny Wzór ogólny
a1 = 1 a1 = 21 − 1 = 1
a2 = 2*1 + 1 = 3 a 2 = 22 − 1 = 3
a3 = 2*3 + 1 = 7 a3 = 23 − 1 = 7
Krok 2. Założenie dla n = k
(co interpretujemy następująco: wzór jest prawdziwy dla n = 1, 2, 3, ... , k)
ak = 2k − 1 = 2*2k−1 + 1
Krok 3. Teza dla n = k + 1
(co interpretujemy następująco: jeśli wzór jest prawdziwy dla n = 1, 2, 3, ... , k, to jest
również prawdziwy dla następnej po k liczby naturalnej, czyli dla n = k + 1)
ak+1 = 2k+1 − 1 = 2ak + 1
Krok 4. Dowód.
ak+1 = 2k+1 − 1 = 2k*2 − 1 = 2k*2 − 2 + 1 = 2(2k − 1) + 1 = 2*ak + 1
co należało wykazać.
a2010 = 22010 − 1
PS. Zapis dowodu jest za bardzo łopatologiczny, ale chciałem, żeby był zrozumiały.
15 sie 13:57

 A(x1,y2)
B(x2,y3)
C(x3,y3)
A(x1,y2)
B(x2,y3)
C(x3,y3)
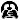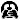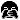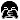

 Zadanie 1 i 3.
As to as, od razu widać po sposobie rozwiązania
Zadanie 1 i 3.
As to as, od razu widać po sposobie rozwiązania  Zadanie 3.
S = (a, b) to środek ciężkości trójkąta, czyli punkt przecięcia jego środkowych.
Zadanie 3.
S = (a, b) to środek ciężkości trójkąta, czyli punkt przecięcia jego środkowych.
 .
W bardziej rozbudowanym rozwiązaniu znalazłby się jeszcze dowód stwierdzenia:
"są to więc potęgi dwójki pomniejszone o 1", np. dowód indukcyjny.
.
W bardziej rozbudowanym rozwiązaniu znalazłby się jeszcze dowód stwierdzenia:
"są to więc potęgi dwójki pomniejszone o 1", np. dowód indukcyjny.