Matura rozszerzona
Koczer: Witam. Zdaje matematykę rozszerzoną. Może jest ktoś chętny na rozwiązywanie zadań z
wszystkich działów oprócz logarytmów i stereometrii]]
braz
28 kwi 20:33
Koczer: sorki za błędy bo przypadkiem mi się wysłało bez edycji

28 kwi 20:34
Koczer: Moze pierwsze zadanie dam z gazety wyborczej z przykladowych zadan matury rozszerzonej:
sin2x+4sin2xcos2x−3cos2x=0
28 kwi 20:36
Mickej: zdajesz rozszerzoną i nie wiesz jak to rozwiązać

?
np można tak skorzystaj z 1 trygonometrycznej
cos
x=1−sin
2x podstaw i uprość jak sie da i zobacz co ci wyjdzie
28 kwi 20:42
Koczer: Nie no ja wiem jak to rozwiazac... ale myslalem ze na poczatek takie wystarczy

28 kwi 20:45
@Basia:
sin2x + 4sin2xcos2x − 3cos2x =
1−cos2x + 4(1−cos2x)cos2x − 3cos2x =
1−cos2x + 4cos2x − 4cos4x − 3cos2x =
−4cos4x +1
1− 4cos4x = 0
(1−2cos2x)(1+2cos2x) = 0
1+2cos2x ≠0 ⇒
1−2cos2x = 0
(1−√2cosx)(1+√2cosx) = 0
dalej już sobie na pewno poradzisz
28 kwi 20:45
Koczer: mi wyszło:
4sin4x−8sin2x+3=0
i teraz:
sin2x=t
4t2−8t+3=0
28 kwi 20:47
Mickej: a ja pojadę tak
sin2x+sin2xcos2x−3cos2x(1−sin2x)=0
sin2x(1+cosx)−3cos2x(cos2x)=0
(1−cos2x)(1+cos2x)−3cos4x=0
1−cos4x−3cos4x=0
4cos4x−1=0
(2cos2x−1)(2cos2+1)=0
(√2cosx−1)(√2cosx+1)(cos2x+1)=0 a dalej to już oczywista oczywistość
28 kwi 20:48
@Basia: Też dobrze. Wynik będzie taki sam.
28 kwi 20:49
Klara: 
ja idento

28 kwi 20:49
28 kwi 20:50
Koczer: to moze ktos da jakies zadanie teraz

28 kwi 20:51
Mickej: tylko że t2 odpada nie dałeś założenia że t∊<0;1>
28 kwi 20:51
Koczer: założenie t∊<0;2π>
28 kwi 20:52
Mickej: wykułem dzisiaj 4 strony A4 na pamięć na prezentacje na polski i już nie mysle

a to założenie t∊<0;2π> jest błędne
28 kwi 20:55
Koczer: ja za polski biore sie po matmie az bo mam 15 maja...

28 kwi 20:57
Koczer: to da ktos kolejne zadanie?

28 kwi 20:57
Mickej: a ja 6 od razu na samym początku
28 kwi 20:57
Mickej:
Masz baw się
Korzystając z definicji, udowodnij że funkcja o równaniu f(x)=x3−x+4 jest rosnąca w przedziale
(1;∞)
poziom trudności średni oceniam na 4 pkt
28 kwi 20:59
Mariusz: może macie ochote na wielomiany


28 kwi 20:59
Mickej: o daj mariusz dodaj jak masz fajne
28 kwi 21:00
Klara:
1sinx − 1sin4x = 0 w przedziale <−π,π>
28 kwi 21:01
Koczer: moga byc wielomiany

28 kwi 21:02
Mariusz: może coś w tym stylu na poczatek, zaraz dam drugie
wykaz że nierówność x6+x4+2x2>=0 jest spełniona przez każdą liczbę rzeczywistą x
28 kwi 21:02
Mickej: Klara fajne zadanie ale strasznie dużo pisania

28 kwi 21:03
Mickej: co do
x6+x4+2x2≥0
x2(x4+x2+2)≥0 a to oczywiste ale co do wykazania to raczej indukcja lub coś w tym stylu a w
takie rzeczy to ja się juz dzisiaj nie bawie
28 kwi 21:06
Klara:
Do zad Mariusza:
x
2( x
4 +x
2 +2) ≥0
x
2 ≥0 dla x€R i x
4 +x
2 +2 ≥0 też dla x€R


28 kwi 21:07
Koczer: x
2(x
4+x
2+2)≥0
nie tak duzo pisania

28 kwi 21:09
Koczer: Dziesiec ksiazek ustawiono w sposob losowy na polce. Oblicz prawdopodobienstwo zdarzenia, ze
trzy okreslone ksiazki znajduja sie obok siebie.
28 kwi 21:13
Klara: zad/
Dla jakiej wartości parametru "m" odwrotność sumy kwadratów
pierwiastków równania
x2 −3mx +m −4=0
jest największa?
28 kwi 21:14
28 kwi 21:14
Koczer: tak?
28 kwi 21:14
Krzysiek: @Basia:
sin2x + 4sin2xcos2x − 3cos2x =
1−cos2x + 4(1−cos2x)cos2x − 3cos2x =
1−cos2x + 4cos2x − 4cos4x − 3cos2x
Zdaje mi się, że masz tu błęda, bo 4(1−cos2x)cos2x to wcale nie jest 4cos2x − 4cos4x, bo
przecież 4*1 to po prostu 4, a nie wiem skąd tam cos wytrzasnęłaś. 4−4cos2x*cos2x, czyli
4−4cos4x tak chyba będzie, tylko co teraz z tym zrobić, jeśli cos2x się nie skrócą i nie
znikną?
28 kwi 21:17
Koczer: a jak zrobić to z odwrotnością sumy kwadratów?
28 kwi 21:18
Mickej: Klara to trygonometri rozwiązanie to
| | 2 | |
x=− |
| π   |
| | 3 | |
28 kwi 21:20
Krzysiek: Koczer, ja inaczej rozumiem to twoje zadanie. Ω owszem 10!, ale A to według mnie będzie 8
możliwych miejsc na położenie tych trzech książek w kolejności (środkowa może być na miejscach
2,3,4,5,6,7,8,9), reszta możliwości to rozstawienie reszty siedmiu książek na miejscach, czyli
7!, co w sumie da 8!
28 kwi 21:29
Koczer: dajcie jeszcze jakies zadania

28 kwi 21:29
Koczer: tak Krzysiek, masz racje

28 kwi 21:30
Mickej: ale nie zapominajcie że te 3 książki zmieniają się też miejscami czyli
8!*3! czyż nie

28 kwi 21:36
@Basia: Zadanie z prawdopodobieństwa.
Koczer całkiem nie trafił.
Krzysiek już bliżej, ale jeszcze nie w dziesiątkę.
Wybieram trzy miejsca obok siebie. 8 sposobów (zgadzam się z Krzyśkiem), ale nie zostało
określone w jaki sposób mają stać te 3 książki czyli mogę je ustawić na 3! sposobów,
pozostałe 7 oczywiście na 7! sposobów
razem: 8*3*7! = 3*8!
28 kwi 21:37
Klara:
Rozwiazać równanie:
x4 +3 − I 3x3 +x I =0
28 kwi 21:48
Mickej: co do zadanie klary rozumiem że odwrotność sumy kwadratów
to coś takiego
| 1 | |
| =max czyli max dla q=min czyli dla wierzchołka |
| 9m2−2m+8 | |
28 kwi 21:48
Mickej: rozwiązania równania to
x=3
x=−3
x=1
x=−1
28 kwi 21:52
Krzysiek: a ja teraz zrozumiałem tak, że jest 10 miejsc na książki i 10 książek, powiedzmy, że a,b,c... i
tak 10 liter i chodzi o to, żeby a,b,c lub b,c,d lub e,f,g stały koło siebie i jeżeli tak, to
A=7!*(wariacja 3 elementów bez powtórzeń ze zbioru 10 elementowego, czyli 10!/(10−3)!
28 kwi 21:53
13LateK: mickej nie rozumiem, możesz jakos twoje rozwiązanie objaśnić


28 kwi 21:59
Mickej: ale które

bo jest ich kilka

28 kwi 21:59
13LateK: czemu masz 1 podzielone przed deltę?
28 kwi 22:00
Mickej: to nie jest delta

to z wzorów viet'a jest
28 kwi 22:02
Klara: Mickej

m=
19 
znajdź błąd

28 kwi 22:04
@Basia:
@ Krzysiek
"trzy określone książki"
czyli np. a,e,i i żadne inne
@ Mickej
Przerywnik w zadaniach rachunkowych
b.: To jeszcze jedno zadanko (dla licealistów): czy istnieje funkcja f:R−>R, która każdą
wartość y∊R przyjmuje dokładnie dwa razy?
28 kwi 22:05
Mickej: no widać jak byk jaki błąd zrobiłem
przy wierzchołku pomnożyłem b*2 a nie a

ale tak to rozwiązanie jest poprawne bo
28 kwi 22:06
Klara:
Mickej

Odp; poprawne do równania z modułem
podaj jak do tego doszedłeś?... niech inni zobaczą

28 kwi 22:07
Klara: Tak , teraz OK

pamietaj o tym na maturze

28 kwi 22:08
Mickej: na ten przerywnik ide się popluskać w wodzie bo już nieprzyjemnie pachnę

28 kwi 22:09
daveustro: chyba dla f(x)=|x| dokładnie dwa razy przyjmuje ten sam y, tak

28 kwi 22:10
daveustro:
28 kwi 22:12
Klara: To teraz takie króciutkie

oblicz 90% liczby
1,2(4)
28 kwi 22:12
13LateK: no jak to mickej... przeciez ten trzeci ułaamek 1/9m2−2m+8 to delta jest
28 kwi 22:20
Bogdan:
f(x)=|x|, wartość y = 0 jest tylko raz, a np. wartość y = −1 ani razu, podobnie jak każdą
wartość y < 0.
28 kwi 22:23
Mickej: według mnie nie istnieje taka funkcja
28 kwi 22:26
Mickej: ale muszę się zastanowić
28 kwi 22:26
Mickej: delta to by było
9m2−4m+16 a to chyba nie to samo co 9m2−2m+8
28 kwi 22:28
Mickej: klara w twoim zadaniu wystarczy usunąć okres

28 kwi 22:29
Klara: Jak usuniesz "okres" ....... to dzieci nie będzie


28 kwi 22:31
Krzysiek: Jak to nie? f(x)=|x|−∞

28 kwi 22:31
Mickej:
f(x)=log
|x|2 sie liczy

28 kwi 22:34
Mickej: funkcja
f(x)=log|x|2 nie jest określona dla całego r ale przyjmuje każdą wartość 2 razy a nie o taki
okres mi chodziło Klaro
28 kwi 22:35
28 kwi 22:36
Mickej: Krzysiek dla −
∞ będzie jeden raz przyjęta wartość tylko

28 kwi 22:36
Mickej: żeby nie było
| | 4 | | 4 | |
1,2(4)=1,2+ |
| + |
| ....... |
| | 100 | | 1000 | |
q={1}{10}
a dale to już chyba każdy wie jak
| | 1 | |
1,2+ |
| ..................... |
| | 9 | |
28 kwi 22:42
Bogdan:
Czy istnieje funkcja f:R−>R, która każdą wartość y∊R przyjmuje dokładnie dwa razy?
Np. f(x) = ctgx dla x ∊ (−π, 0)⋃(0, π)
28 kwi 22:42
Mickej: heh faktycznie
28 kwi 22:43
Klara: 
28 kwi 22:43
ciemny :(:
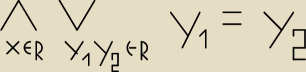
28 kwi 22:51
ciemny :(: wiec bedzie to f(x)=|x| oraz każda parzysta potęga iksa np. f(x)=x2 lub f(x)=x4 ...
28 kwi 22:53
Mickej: To żeby Klara się nie czepiała
x4 +3 − I 3x3 +x I =0
x4 +3 = I 3x3 +x I
3x3+x=x4+3 lub 3x3+x=−x4−3 a dalej to już prosty rozkład
na czynniki
28 kwi 22:53
Bogdan:
Nie wiem, czy ten problem już kiedyś tu się pojawił, warto go jednak przed maturą
przypomnieć.
Mając dane liczby; a, b, c rozwiązać równanie: asinx + bcosx + c = 0, a ≠ 0, b ≠ 0, c ≠ 0.
Należy podać ograniczenia, schemat postępowania oraz rozwiązanie.
28 kwi 22:54
Mickej: ciemny ale x2 nie przyjmuje wartosci −1 np a ma przyjmować każdą wartość 2 razy czyli tak jak
Bogdan proponuje ctgx w danym przedziale lub mój logarytm
28 kwi 22:54
ciemny :(: dodatkowo jeszcze dając " − " przed x to bedzie tak samo


tylko ramiona w dól...
28 kwi 22:54
ciemny :(: Aha

28 kwi 22:56
@Basia: Ona ma być określona na całym zbiorze R.
Przykład Bogdana nie spełnia tego warunku.
Taka, która każdą swoją wartość przyjmuje dokładnie dwa razy dałoby się chyba znaleźć.
(ale pewna nie jestem)
Jeżeli jednak ma być dodatkowo surjekcją czyli każdą wartość rzeczywistą przyjmować
dokładnie dwa razy to sprawa staje się nieco bardziej skomplikowana.
b. tego nie sprecyzował.
28 kwi 22:56
ciemny :(: Mickej ale po przeniesieniu wart. bezwzgl. zapomniales przed nia minusa

28 kwi 22:57
ciemny :(: o przepraszam moja pomylka MICKEJ

sorry
28 kwi 22:59
@Basia: Gdyby nie musiała być określona na całym R to byłoby bardzo proste.
itd.itd.
ale one nie są określone dla x=0 i nie spełniają warunków zadania
28 kwi 23:00
Mickej: Znowu zadanie za które nie wiem jak się zabrać

28 kwi 23:00
Mickej: co do tego zadania
asinx + bcosx + c = 0 to mogę sobie podstawić pod sin i cos jakieś wartosci


28 kwi 23:07
Bogdan:
Świadomie zrezygnowałem z przyjęcia dla x zbioru R ograniczając dziedzinę
przedziałem x∊(−π, 0)⋃(0, π) dla funkcji f(x) = ctgx chcąc pokazać przykład funkcji
przyjmującej każdą wartość y dokładnie 2 razy.
28 kwi 23:07
ciemny :(: To musi byc cos takiego ze prosta x1 = − x1 ale nie wiem czy takie cos istnieje
28 kwi 23:08
Bogdan:
asinx + bcosx + c = 0
Nie chodzi o podstawienie jakiejś wartości, ale o pokazanie schematu rozwiązywania,
czyli algorytmu dla tego równania.
28 kwi 23:09
Mickej: ciemny ty to jesteś ciemny

28 kwi 23:09
Mickej: aha chyba że tak
28 kwi 23:12
ciemny :(: −x4−3−3x3−x = 0
x3(−x−3)+(−x−3) = 0
(x3 +1) (−x−3) = 0
x3=−1 x=−3
x=−1
ale jak zrobic ta czesc :
x4 + 3 = 3x3 + x
28 kwi 23:13
ciemny :(: to zes mnie podsumował

28 kwi 23:13
Mickej:
asinx+bcosx+c=0
asinx+c=−bcosx ()2
a2sin2x+2acsinx+c2=b2cos2x
a2sin2x+2acsinx+c2=b2−b2sin2x
(a2+b2)sin2+2acsinx+c2−b2=0
sin=t t∊<−1;1>
(a2+b2)t2+2act+c2−b2=0
Δ=4(ac)2−4(a2+b2)(c2−b2)
28 kwi 23:17
Mickej: czy chodziło o coś w tym stylu

?
28 kwi 23:17
@Basia: Nie jestem pewna czy dobrze interpretuję to zadanie, ale moim zdaniem takiej określonej na
całym R nie ma.
28 kwi 23:19
dpelczar: asin(x) + bcos(x) +c = 0
asin(x) = −c − bcos(x)
TYLKO CO DALEJ...

28 kwi 23:20
Mickej: x4 + 3 = 3x3 + x
x4 + 3 − 3x3 − x=0
x3(x−1)−1(x−3)=0
(x3−1)(x−3) tak
28 kwi 23:25
Klara: dpelczar
obustronnie podnieść do kwadratu

następnie skorzystać z jedynki tryg.
i doprowadzić równanie do jednej zmiennej np; sinx
28 kwi 23:37
Mickej: czy mojego algorytmu nikt nie widzi czy nikt nie chce powiedzieć czy jest dobry czy zły

?
28 kwi 23:38
Klara: Mickej

w tym równaniu rozpatrzeć przedziałami
tylko dla x≥0 i x<0
bo 3x
3 +x = x( 3x
2 +1)....... dalej już wiesz

28 kwi 23:39
Klara: Oooo Mickej

.... mamy te same
algorytmy 
28 kwi 23:41
Mickej: mi takich rzeczy nie musisz tłumaczyć

przecież rozwiązałem to wyrzej
28 kwi 23:43
Klara: Oczywiście pomyłkowo napisałam ,że
c przenosimy na prawo
ma być bcosx na prawo

28 kwi 23:44
daveustro: Mickej, wyjdzie −3, −1, 1, 3

x
4 − 3x
3 − x + 3 = 0
(x
3 − 1) (x − 3) = 0
x = 1 v x = 3
a '−1' i '−3' to z tego drugiego założenia Ci wyjdzie
zgadza się?

28 kwi 23:44
Mickej: tak

taki wynik podałem jakieś 40 postów temu
28 kwi 23:44
28 kwi 23:45
Mickej: no no

ale równania wole liczyć z tego że
|a|=b to
a=b lub a=−b
szybciej niż rozpatrywać na przedziały

28 kwi 23:46
daveustro: no więc w czym tkwi problem?
w ogóle skąd Ci się wzięło
x3(x−1)−1(x−3)=0
x3 (x − 1) − 1(x − 3) = x4 − x3 −x +3
czyli trochę brakuje... a konkretnie −2x3
28 kwi 23:47
Klara:
Do Mickej

28 kwi 23:47
daveustro: Klara dzięki za wsparcie

28 kwi 23:48
Mickej: nie patrzyłem co pisze

myślałem nad czymś innym

28 kwi 23:48
Mickej: Hmmm nie zaproszę was na naszej klasie
28 kwi 23:49
daveustro: a co do przedziałów to się ich tak od pierwszej klasy liceum nauczyłem i w sumie najłatwiej mi
jest tak chyba

i (jak widać) skuteczniej

w ogóle skąd masz dobre wyniki przy złych
obliczeniach?


28 kwi 23:49
daveustro: cholera, jak ja się pokażę z tak marną liczbą znajomej na naszej klasie rodzinie

Mickej nie
rób mi tego

Mam nadzieję, że chociaż Klara mnie wspomoże, żeby się nie wstydzić przed
familią ubogiej listy...

28 kwi 23:51
Mickej: w pamięci sobie policzyłem ale źle przepisałem

Ludzie nie akceptujcie jego zaproszeń na
naszej−klasie.pl
28 kwi 23:52
Mickej: szukałem Klara ale nie znalazłem:( na n−k
28 kwi 23:54
dpelczar: Nie wazne ile masz znajomych na naszej klasie − mozesz ich miec tysiące...
Wazne jakich tych znajomych masz − NIE LICZY SIE ILOSC

LICZY SIE JAKOŚĆ

28 kwi 23:54
Mickej: heh to jasna sprawa przecież

28 kwi 23:55
Bogdan:
asinx + bcosx + c = 0
asinx + bcosx = −c dzielimy obustronnie przez a
| | b | | sinα | |
Podstawienie: |
| = tgα = |
| |
| | a | | cosα | |
| | sinα | | −c | |
sinx + |
| * cosx = |
| mnożymy obustronnie przez cosα |
| | cosα | | a | |
| | −c | |
sinx cosα + sinα cosx = |
| * cosα |
| | a | |
| | −c | | −c | |
Jeśli |
| * cosα ∊ <−1, 1> to przyjmujemy |
| * cosα = sinβ, |
| | a | | a | |
| | −c | |
jeśli |
| * cosα nie należy do przedziału <−1, 1> , to równanie jest sprzeczne. |
| | a | |
sin(x + α) = sinβ
x + α = β + k*2π lub x + α = π − β + k*2π
Przykład:
4sinx + 5cosx − 6 = 0 dzielimy obustronnie przez 4
| 5 | | sin51o20' | |
| = tg51o20' = |
| |
| 4 | | cos51o20' | |
| | sin51o20' | | 3 | |
sinx + |
| * cosx = |
| mnożymy obustronnie przez cos51o20' |
| | cos51o20' | | 2 | |
| | 3 | |
sinx cos51o20' + sin51o20' cosx = |
| * cos51o20' |
| | 2 | |
| 3 | |
| * cos51o20' = 1,25 * 0,6248 = 0,9372 = sin69o35' |
| 2 | |
sin(x + 51
o20') = sin69
o35'
x + 51
o20' = 69
o35' + k*360
o lub x + 51
o20' = 180
o − 69
o35' + k*360
o
x = 18
o15' + k*360
o lub x = 59
o05' + k*360
o
28 kwi 23:55
Mickej: dlatego Klare zaakceptuje w swoich znajomych a ciebie już nie

28 kwi 23:55
Klara: A ja własnie zaaakceptuję

dawaj namiary
daveustro
tylko jak mnie zobaczysz , to nie spadnij z fotela


28 kwi 23:56
28 kwi 23:57
Mickej: widzę właśnie Hmm w sumie tak bym nie kombinował ale już będę wiedział na przyszłość jak to
robić
28 kwi 23:58
Klara: Takiego zad. na maturze i tak nie będzie

Musiałaby trwać co najmniej .... 5godzin pisania
29 kwi 00:01
Mickej: dobra spadam

a wy już dzieci też się zbierajcie do łóżeczek bo późna godzinka już jest
29 kwi 00:02
dpelczar: Dzieki za kolejny wspolny dzien z zadaniami i z wasza pomocą

to do zobaczenia

Dobranoc
29 kwi 00:07
29 kwi 00:11
dpelczar: A ja mam takie zadanie − nie potrafiłem go zrobić bo Δ pochodnej jest mniejsza od zera...

Rozwiązać:
x
3 − 2,5x
2 + 5x −2 = 0 Wiem ze trzeba skorzystac z pierwiastków wymiernych − powiedzcie po
koleji jak...

Nigdy tego nie obiłem i dlatego nie wiem...
29 kwi 10:31
29 kwi 10:41
tim: Mogę ja?

. Matury nie piszę (za 5 lat), ale mogę?

29 kwi 10:47
tim: (za 4 już

*)
29 kwi 10:48
tim: Nie ma sprzeciwów, więc piszę.
Korzystając z wzoru na długość środkowej wyliczamy, że:
długość środkowej opadającej na bok c wynosi:
długość środkowej opadającej na bok a wynosi:
Skoro
d
1 =d
2 d
1, d
2, a, b, c ∊ dodatnie
zatem
| 1 | | 1 | |
| √2a2 + 2b2 − c2 = |
| √2c2 + 2b2 − a2 *2 |
| 2 | | 2 | |
√2a2 + 2b2 − c2 =
√2c2 + 2b2 − a2 2
2a
2 + 2b
2 − c
2 = 2c
2 + 2b
2 − a
2
3a
2 = 3c
2 :3
a
2 = c
2 √
a =
29 kwi 10:53
daveustro:  tim
tim dawaj

29 kwi 10:53
daveustro: Możesz rysunek? Łatwiej będzie zrozumieć

29 kwi 10:54
Mickej: Delpczar co do tego równania mówiłem ci już że pierwiastkiem jest
x={1}{2} a dalej to możesz dzielić lub inne czary odprawiać

29 kwi 10:56
tim:
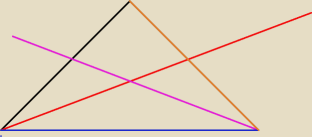
różowe − d
1
czerwone − d
2
niebieskie − b
czarne − c
pomarańczowe/brązowe − a
29 kwi 10:56
29 kwi 10:57
daveustro: Mickej a jak ten pierwiastek znalazłeś?
29 kwi 10:57
BigMax:
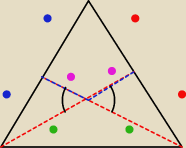
A można to zrobić tak? :
Kolorowe kropki oznaczają odcinki równej długości.
Miedz środkowymi jest zaznaczony kąt α. Środkowe przecinają się w środku ciężkości trójkąta
który dzieli każda środkową w stosunku 2:1 a jako że środkowe mają takie same długości myślę,
że te dwa trójkąty są identyczne ( cecha bok bok kąt − coś takiego) więc jeżeli mają połowy
boków takie same to boki też są równej długości. Jak sądzicie?
29 kwi 11:07
BigMax: Ja mam problem z takim zdaniem:
Na okręgu zaznaczono sześć równych punktów. Następnie w sposób losowy poprowadzono trzy
cięciwy, których końcami są zaznaczone punkty. Oblicz prawdopodobieństwo otrzymania trójkąta.
Zasiadłem do tego i na początku obliczyłem ile można zrobić w takim wypadku prostych:
| | | |
i teraz liczyłem Ω = | = 13*7*5 |
| | |
Ale liczby zdarzeń A nie mogę policzyć liczby zdarzeń A
29 kwi 11:17
Krzysiek: | | 1 | |
Twoje zadanie daveustro: x3 − 2,5x2 + 5x −2 = 0 ma pierwiastek |
| bo najpierw sprawdzamy |
| | 2 | |
wszystkie dzielniki wyrazu wolnego, czyli −2, czyli 1,−1,2,−2. Nie wychodzi zero, to patrzymy
na ułamki pierwszego wyrazu(w tym wypadku 1, którego oczywiście normalnie nie piszemy przed
| | 1 | | 1 | | 1 | |
x3), więc |
| i − |
| . Dalej już proste, dzielisz cały wielomian przez x− |
| |
| | 2 | | 2 | | 2 | |
schematem hornera i cacy.
29 kwi 11:39
Mickej: już mu to 2 razy mówiłem ale chyba nie wie jak się zabrać za dzielenie

29 kwi 11:47
29 kwi 11:50
Bogdan:
Krzysiek, jest trochę inaczej, patrz tu
121.
W mianowniku wyrażenia jest dzielnik współczynnika przy najwyższej potędze,
a nie dzielnik wyrazu wolnego.
x
3 − 2,5x
2 + 5x − 2 = 0 mnożymy obustronnie przez 2.
2x
3 − 5x
2 + 10x − 4 = 0
p € {1, −1, 2, −2, 4, −4}
q € {1, −1, 2, −2}
| p | | 1 | | −1 | |
| € {1, −1, |
| , |
| , 2, −2, 4, −4} |
| q | | 2 | | 2 | |
29 kwi 13:07
Krzysiek: Racja. Troche to dziwne, bo jak się trafi na jakiś złośliwy przykład to może i godzinę szukać
tej liczby, bo jak nie wyjdzie z pomnożenia całego wielomianu przez 2 tak jak to zrobiłeś, to
może wyjdzie jak pomnoże przez 32 i wtedy mam możliwości do sprawdzenia na cały dzień. Mam
nadzieje, że na maturze zawsze tak dobierają przykłady zeby się ładnie rozwiązywały.
29 kwi 13:14
Krzysiek: Bogdan, to zadanie co rozwiązywałe, skąd to się wzięło?
| | b | | sinα | |
Podstawienie: |
| =tgα= |
|
|
| | a | | cosα | |
Te litery a,b,c to boki trójkątów i można je tak wykorzystywać?
29 kwi 13:23
Bogdan:
a, b, c to nie boki trójkąta. To liczby będące współczynnikami równania asinx + bcosx + c = 0,
tak, jak w równaniu kwadratowym ax
2 + bx + c = 0 oznaczenia a, b, c to współczynniki
| | ax + b | |
albo |
| oznaczenia a, b, c, d to współczynniki. |
| | cx + d | |
29 kwi 13:54
Bogdan:
Podałem pewien algorytm rozwiązywania równania trygonometrycznego i przyjąłem
oznaczenia a, b, c. Mogłem przyjąć inne, np.: msinx + ncosx + k = 0 albo psinx + qcosx + t = 0.
29 kwi 13:56
Mickej: No ile można czekać gdzie ci maturzyści z zadankami

29 kwi 15:24
tim: No właśnie.. cisza taka.. [przed burzą]
29 kwi 15:24
Mickej: Gdzie moja kompanka Klara Hmmmm

29 kwi 19:10
Krzysiek: Wyznacz wszystkie wartości k ∈ R , dla których pierwiastki wielomianu
W(x) = (x2 − 8x +12)⋅(x − k) są trzema kolejnymi wyrazami rosnącego ciągu
geometrycznego.
Było takie?
30 kwi 11:28
Mickej: nie nie było ale coś za proste jak na rozszerzony

30 kwi 11:39
Krzysiek: z próbnej z 2006

najpierw go źle zrozumiałem i myślałem, że trudne, a jak rzuciłem okiem na
odpowiedzi to aż się przestraszyłem, że to o to chodziło.
30 kwi 11:53
imię lub nick: Przedstaw wielomian W(x)=x4−2x3−3x2+4x−1 w postaci iloczynu dwóch wielomianów stopnia drugiego
o współczynnikach całkowitych i takich że współczynniki przy drugich potęgach są równe 1.
proste ale jakoś nie umiem wpaść jak to rozłożyć

30 kwi 11:56
Kris_garg: Krzysiek jaka jest odpowiedz do twojego ostatniego zadania ?
30 kwi 12:00
30 kwi 12:04
imię lub nick: ooo dzięki

30 kwi 12:07
Mickej: ok to wrzucać zadanka i jedziemy jakie macie

30 kwi 12:14
imię lub nick:
nie czaje jak z x2(x−1)2 robi się (x2−x)2
jak to jest?
30 kwi 12:15
Mickej: ja też wrzuce tylko podajcie jakiś dział z jakiego chcecie zadanko

30 kwi 12:16
Mickej: tak

a
2*b
2=(a*b)
2 rozumiesz


?
30 kwi 12:17
imię lub nick: aaa

no tak
to daj jakieś trudne zadanko z prawdopodobieństwa
30 kwi 12:20
Mickej: zacznijmy od czegoś prostego

Wyznacz P(A) wiedząc że P(A)*P(A')=0,25
też coś wrzućcie bo już mi się zadanka skończyły

30 kwi 12:24
imię lub nick: 12 ?
30 kwi 12:29
imię lub nick: dobra już jestem pewien

30 kwi 12:31
Mickej:
W urnie jest 5 kuli białych i 2 kule czarne. Wyciągnięto losowo bez zwracania 2 kule. Oblicz
prawdopodobieństwo wyciągnięcia kuli czarnej z pozostałych kul.
patrze i patrze i stwierdzam że nie mam trudnych zadań z tego działu
30 kwi 12:31
Bogdan:
Proponuję zadania z poprzednich matur.
Zadanie maturalne z 1999 r. podobne do pokazanego wyżej zadania Krzyśka.
Zad1 (1999).
Dana jest funkcja f(x) = x3 − (p + 3)x2 − 4x.
Dla jakiej wartości parametru p jeden z pierwiastków równania jest średnią arytmetyczną
pozostałych pierwiastków?
Zamieszczę jeszcze zadanka z innych lat.
30 kwi 12:32
Mickej:
A to może jeszcze takie
Rzucamy dwukrotnie sześcienną kostką do gry. Rozpatrzmy zdarzenia:
A−suma wyrzuconych oczek jest 8
B−w pierwszym rzucie wyrzucono liczbę nieparzystą
Czy zdarzenia A i B są niezależne

?
30 kwi 12:35
imię lub nick: są trudniejsze − z koniecznością wykorzystania wzoru na prawdopodobieństwo sumy zdarzeń itp.
30 kwi 12:36
Mickej: o to bierzemy się za to

30 kwi 12:37
Mickej: dziwne to zadanie Bogdana

30 kwi 12:45
Krzysiek: ale wiecie, że na maturze w tym roku prawdopodobieństwo jest bardzo okrojone? Nie ma żadnych
zdarzeń niezależny, prawdopodobieństwa warunkowego i całkowitego?
Mickej − jak zrobić to Twoje z kulami?
30 kwi 12:46
Mickej: najpierw pobawmy się zadaniem Bogdana a później podam ci rozwiązanie krok po kroku

30 kwi 12:49
Krzysiek: ok, na razie tyle wymyśliłem: jeśli wyciągniemy x przed nawias to na pewno 0 jest jednym z
rozwiązań i mamy równanie kwadratowe z parametrem, które ma mieć dwa pierwiastki. Mamy więc 3
| | x1+0 | |
pierwiastki, z których jeden jest średnią dwóch pozostałych. Więc |
| =x2, tak? |
| | 2 | |
30 kwi 12:54
Bogdan:
Wskazówka:
x
1, x
2, x
3 − pierwiastki równania.
Trzeba wziąć pod uwagę wszystkie przypadki:
| | x2 + x3 | | x1 + x3 | | x1 + x2 | |
x1 = |
| , x2 = |
| , x3 = |
| . |
| | 2 | | 2 | | 2 | |
30 kwi 12:59
Krzysiek: x(x
2−(p+3)x−4)
c=−4
więc iloczyn dwóch pierwiastków będzie ujemny, więc mają one różne znaki.
30 kwi 13:00
Mickej: miałem problem bo jestem baran delta wyszła z p i delta po p wychodziła ujemna i wziołem to tak
jak by nie było pierwiastków w nawiasie

30 kwi 13:02
Krzysiek: | | x2+x3 | |
1) 0= |
| , więc x3=−x2
|
| | 2 | |
| | x3+0 | |
2) x2= |
| , czyli x3=2x2
|
| | 2 | |
| | x2+0 | |
3) x3= |
| , czyli x2=2x3
|
| | 2 | |
o ile dobrze rozumiem, to opcje 2 i 3 znaczą to samo, że jeden pierwiastek od drugiego ma być
dwa razy większy(bo ich kolejność nie ma znaczenia)
30 kwi 13:06
imię lub nick: czyli x=0 lub x=2 lub x=−2 dla p = −3 tak?
30 kwi 13:07
Krzysiek: to liczymy:x
3+−x
2
wzory Viete'a:
−b=p+3
p+3=0
p=−3
30 kwi 13:10
imię lub nick: 
wtedy tylko średnia pierwiastków kwadratowego jest równa temu trzeciemu

30 kwi 13:10
Krzysiek: wyszły pierwiastki −2,0,2
Chyba wyszło, nie? No przecież tylko jeden pierwiastek ma być średnią dwóch innych i tym
pierwiastkiem jest 0
30 kwi 13:12
Mickej: ja mam tak samo jak krzysiek tylko teraz kombinuje nad wyznaczeniem wartosci p dla przypadku 2
i 3 które on napisał
30 kwi 13:13
Krzysiek: Jak probowałem liczyć inne możliwości, to mi wychodziły sprzeczności jakieś, x2=−4, więc to co
policzyłem to chyba jedyne rozwiązanie. Bogdan, osądź...
30 kwi 13:14
Krzysiek: x
2=2x
3
wzory Viete'a:
c=−4
a=1
2x
32=−4
x
2=−2, czyli x nie istnieje
30 kwi 13:17
Mickej: ładny mason to zadanie

30 kwi 13:17
Krzysiek: Jeśli mi dobrze wyszło to fajne to zadanie, bardziej na kombinowanie niż wiedzę, a że u mnie z
wiedzą kiepsko, to przynajmniej pokombinować na maturzę mogę.
30 kwi 13:18
Mickej: ale tak sie nie robi jak ty zrobiłeś

wystarczy że podstawił byś sobie to −2 i 2 to nie
wyjdzie ci według tego co zrobiłeś
30 kwi 13:21
Krzysiek: Nie rozumiem, możesz pokazać gdzie jest ten błąd. Wyznaczyłem p=−3, dla którego jeden z
| | −2+2 | |
pierwiastków, czyli 0 jest średnią dwóch pozostałych, czyli −2 i 2, bo |
| =0. |
| | 2 | |
30 kwi 13:26
Mickej: aha ale to wyszło jak 0 było srednia

no w tym twoim coś jest

30 kwi 13:26
Mickej: to uznajemy że tylko −3 jest rozwiązaniem

30 kwi 13:27
Krzysiek: A co, 0 nie może być średnią dwóch liczb? ja nic innego nie wycisnę z tego zadania, a skoro
znalazłem to o co prosili i zgadza się jeśli podstawię to p to co mam jeszcze innego robić.
Możemy jeszcze poczekać na Bogdana, bo on na pewno ma odpowiedź do tego zadania, a w
międzyczasie możesz mi wytłumaczyć to Twoje z kulkami, co Ty na co?
30 kwi 13:29
Mickej: Moimi kulkami trochę się będę krępował mówiąc o nich ale jak chcesz podam ci co trzeba zrobić i
sam rozwiążesz

30 kwi 13:32
Krzysiek: No nie za bardzo radzę sobie z takimi dwuetapowymi zadaniami z prawdopodobieństwa...
30 kwi 13:34
Krzysiek: Chyba wiem, drzewkiem się to da dosyć łatwo zrobić.
30 kwi 13:37
Mickej: Skorzystamy z wzoru na prawdopodobieństwo całkowite i wprowadzimy oznaczenia
A
1−losujemy 2 kule białe
A
2−losujemy 2 kule czarne
A
3 losujemy 1 taką 1 taką
B− następna wylosowana kula jest czarna
dalej wyznaczamy A
1 ,A
2 A
3 co nie jest chyba trudne podam ci na wszelki wypadek ile
wynoszą

znamy stan urny jaki jest po zajściu każdego z możliwych zajść teraz prawdopodobieństwo
warunkowe obliczasz i już jest

30 kwi 13:37
Krzysiek: | | 10 | | 2 | | 10 | | 1 | | 2 | |
P(A)= |
| * |
| + |
| * |
| = |
| |
| | 21 | | 5 | | 21 | | 5 | | 7 | |
30 kwi 13:41
Mickej: dokładnie

30 kwi 13:43
Mickej: nie wiem co oni dzisiaj z tymi ciągami mają pola też dała wielomian z ciągiem

30 kwi 13:43
Bogdan:
Odp.: p = −3
f(x) = x
3 − (p + 3)x − 4x ⇒ f(x) = x(x
2 − (p + 3)x − 4), a = 1, b = −(p+3), c = −4
Równanie x
2 − (p + 3)x − 4 ma 2 rozwiązania ⇔ Δ ≥ 0.
Δ = p
2 + 6p + 9 + 16 = p
2 + 6p + 25, Δ
p = 36 − 100 < 0, a więc p ∊ ℛ
x
1 = 0
| | x2 + x3 | |
0 = |
| ⇒ x2 + x3 = 0 ⇒ p + 3 = 0 (z wzorów Viete'a) ⇒ p = −3 |
| | 2 | |
| | 0 + x3 | |
x2 = |
| ⇒ x3 = 2x2 ⇒ x2*x3 = 2x22 ⇒ −4 = 2x22 (z wzorów Viete'a) |
| | 2 | |
sprzeczność.
| | 0 + x2 | |
x3 = |
| ⇒ x2 = 2x3 ⇒ x2*x3 = 2x32 ⇒ −4 = 2x32 (z wzorów Viete'a) |
| | 2 | |
sprzeczność.
30 kwi 13:46
Mickej: więc Krzyś zrobił dobrze

30 kwi 13:48
Krzysiek: Wyznacz wszystkie wartosci parametru m, dla których układ równań
x+(2−m)y=1
x−y=−2
ma rozwiązanie (a;b) spełniające warunek a*b>0
30 kwi 15:11
blebleble: | | px −3 | |
Funkcja homograficzna f jest okreslona zorem f(x) = |
| gdzie p ∊R jest parametrem i |
| | x−p | |
|p|≠
√3
| | m | |
a) dla p=1 zapisz wzor funkcji w postaci f(x) = k+ |
| gdzie k oraz m sa liczbami |
| | x−1 | |
rzeczywistymi
b) wyznacz wszystkie wartosci parametru p, dla ktorych w przedziale (p ; +
∞) funkca f jest
malejąca
30 kwi 18:42
Doma: Hej

Zapisz w postaci ułamka ile waży cukier
5gram ile to dekagramów
6 maj 20:21
Michał Szczotka: 
6 maj 20:22
Doma: ηi∊ j∊st to śmi∊szη∊
6 maj 20:25
Doma: Śmiej się puki możesz

7 maj 15:01
Doma: Ej a teraz do wszystkich

Moge pomóc w różnych ćwiczeniach lecz jak ktoś mi pomoże

7 maj 15:02
Gienia !!: A kto wie takie zadanie

1.Wpisz odpowiednie ułamki !
390 dni to ........ roku zwykłego
7 maj 15:05
Gienia !!: Czekam na odp . jeśli mnie tu nie będzie a ktoś zna odp to niech pisze na moje gg !3791361
7 maj 15:09
Gienia !!: Prosze was odpisujcie mi zależy mi na tym

7 maj 15:14
C:
13
−−−−
12
7 maj 15:18
7 maj 15:21
Gienia !!: α⊂∊∊∊∊∊∊ϱ
7 maj 15:22
7 maj 15:22
tim: Witaj Eta

7 maj 15:27
Eta: 
Timuś

7 maj 15:29
XxNikUsIaxDxX:
7 maj 15:29
XxNikUsIaxDxX: heh.. elo

'' ; **
7 maj 15:30
tim: Co za powitanie

Skończę obiadek i może jakieś zadanko się dla mnie pojawi.. Hm?
7 maj 15:31
XxNikUsIaxDxX:
7 maj 15:32
7 maj 15:33
XxNikUsIaxDxX: ta może zadam ci 1x1 =
7 maj 15:34
7 maj 15:34
7 maj 15:35
tim: Ale to po obiadku (za dwie minuty)
7 maj 15:35
Eta: Pomyślałam ,że "zwykły" ... to nie przestępny

!

7 maj 15:36
XxNikUsIaxDxX: .
7 maj 15:42
malwinkaxdlolżalkocham: cześć

mam zadanie i nie umie jego rozwiązać to takie !
5
−−−−
5 =
6
−−−−
5 =
7
−−−−−
5 =
13
−−−−−−−−
5 =
18
−−−−−−
5 =
prosze odpiszcie mi

7 maj 15:47
mika:
7 maj 15:47
7 maj 15:49
mika: elo
7 maj 15:49
malwinkaxdlolżalkocham: nie

7 maj 15:50
malwinkaxdlolżalkocham: pomoże mi ktoś ?
7 maj 15:51
tim: która klasa
7 maj 15:53
malwinkaxdlolżalkocham: π
7 maj 16:04
malwinkaxdlolżalkocham: 5 a co ?
7 maj 16:05
malwinkaxdlolżalkocham:
7 maj 16:09
malwinkaxdlolżalkocham: α
7 maj 16:13
malwinkaxdlolżalkocham: :(
7 maj 16:14
malwinkaxdlolżalkocham: δ
7 maj 16:16
Kris_garg: Trójkąt równoraminnny ostrokątny ABC o podstawie AB jest wpisany w okrąg o równaniu
x2 + y2 = 25 . Punkty A i B leża na prostej y = x − 5.
a) Oblicz współrzędne punktów A, B, C
b) Oblicz katy trójkąta ABC
7 maj 18:49
Kris_garg: Dane sa punkt A = (−4 ,32 ) B = (−36 ,16 ) Wykaż że koło o średnicy AB jest zawarte w II ćw.
prostokatnego układu współrzędnych?
7 maj 18:51
Kris_garg: Dany jest ostrosłup prawidłowy trójkątny , w którym dł krawędzi podstawy = a . Kąt miedzy
krawędzią boczna a krawędzią podstawy = 45 . Ostrosłup przecięto płaszczyzna przechodząca
przez krawędź podstawy i środek przeciwległej jej krawędzi bocznej. Sporządź rysunek i oblicz
pole przekroju?
7 maj 18:55
8 maj 08:28
Kris_garg: 

8 maj 08:34
Kris_garg: α
8 maj 08:37
Kris_garg: φωiαzdα ρoρu ' lili '
8 maj 19:06
9 maj 01:57
Eta:
Podpowiadam zad1/ dla Kris−garg
9 maj 02:08
Eta:
zad1/ A( −4, 32) B( −36,16)
IABI −−− średnica , więc S −− okręgu to środek odcinka AB
| | −4 −36 | | 32 +16 | |
zatem xS= |
| yS= |
|
|
| | 2 | | 2 | |
S( −20, 24)
r=IASI=IBSI = policz......... powinno wyjść r = 8
√5
zatem S€I IIćw. a promień r = 8
√5
czyli 8
√5<20 i 8
√5 < 24 więc okrąg musi leżeć w IIćw.
bo odległość S od obydwu osi jest większa od promienia
9 maj 02:15
Eta:
Teraz zad1/ ( poprzednie to było zad2/

9 maj 02:18
Eta:
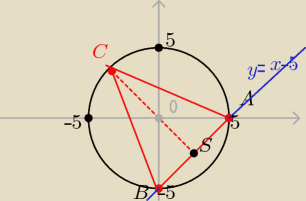
rozwiąż układ równanń prostej y = x −5 i okregu x
2 +y
2 = 25
otrzymasz punkty: A( 5,0) i B( 0,−5)
środek S odcinka AB też wyliczysz S(
52,
52)
prosta CS jest prostopadła do prostej AB i zawiera punkty S i O
bo trójkat jest równoramienny
więc równanie prostej CS : y = −x
rozwiązując układ równań prostej SC i okregu :
otrzymasz dwa punkty C
1 i C
2
Z treści zad. wiesz ,że trójkąt jest ostrokatny więc już chyba będziesz wiedzieć
który punkt C przyjąć z odp:
Jeżeli chodzi o katy tego trójkata , to prosto:
skoro jest równoramiennym więc najprościej wyliczyć kąt między ramionami
czyli <ACB bo kąty przy podstawie wtedy łatwo policzysz
zatem kąt C najłatwiej policzyś ze wzoru sinusów bo masz R −− okręgu
| | IABI | |
zatem: |
| = 2R policz IABI i obliczysz <C
|
| | sinC | |
powodzenia ..... to już banał

zad..... z ostrosłupem? ..... narysuję Ci rysunek .... i powinno pójść gładko

9 maj 02:42
9 maj 02:44
Eta:
Idę na herbatkę

9 maj 02:45
Eta:
Basia pewnie już śpi

Zad 3/ Rysuję

9 maj 02:50
Eta:
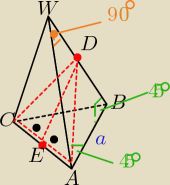
Przekrojem jest trójkat równoramienny ACD
gdzie podstawa ICAI = a i wysokością jest IDEI
ΔABW −−− jest prostokątny i równoramienny jednocześnie
więc krawędż boczna IBWI= U{a
√2{2}
bo a jest przekątną kwadratu o boku IBWI
Z ΔADW prostokątnego z tw. Pitagorasa wylicz długość IADI
następnie z trójkata EAW −− prostokatnego też z tw. Pitagorasa
wylicz IDEI −−− czyli wysokość ΔCAD
podstaw do wzoru na pole
P=
12a*IDEI ...... i to wszystko

Dobranoc Wszystkim

.... idę też do spanka!
9 maj 03:12
Kris_garg: Eta: dziękuje za pomoc w zadaniach

ale mam problem z wyliczeniem współrzędnych C jak możesz
to proszę o pomoc
9 maj 19:22
Eta:
Witam

Jaki problem? rozwiazujesz układ równań:
y= − x i x
2 +y
2 = 25
to x
2 + x
2 = 25 => 2x
2 = 25
więc C
1(
5√22,
−5√22)
C
2(
−5√22,
5√22)
Już z rys. widać ,że skoro trójkąt jest ostrokątny to tylko dla C
2
bo dla C
1 −−−− jest rozwartokątny
to wszystko

10 maj 00:13
Kris_garg: Ale mialem zacmienie wczoraj o ten błysk mi chodziło zapomniałem podnisc −x do
2 i mi nic nie
chciało wyjsc , jeszcze raz wielkie dzieki

10 maj 09:29

 ?
np można tak skorzystaj z 1 trygonometrycznej
cosx=1−sin2x podstaw i uprość jak sie da i zobacz co ci wyjdzie
?
np można tak skorzystaj z 1 trygonometrycznej
cosx=1−sin2x podstaw i uprość jak sie da i zobacz co ci wyjdzie

 ja idento
ja idento

 a to założenie t∊<0;2π> jest błędne
a to założenie t∊<0;2π> jest błędne
















 bo jest ich kilka
bo jest ich kilka
 to z wzorów viet'a jest
to z wzorów viet'a jest
 m= 19
m= 19  znajdź błąd
znajdź błąd 
 ale tak to rozwiązanie jest poprawne bo
ale tak to rozwiązanie jest poprawne bo
 Odp; poprawne do równania z modułem
podaj jak do tego doszedłeś?... niech inni zobaczą
Odp; poprawne do równania z modułem
podaj jak do tego doszedłeś?... niech inni zobaczą 
 pamietaj o tym na maturze
pamietaj o tym na maturze 



 oblicz 90% liczby 1,2(4)
oblicz 90% liczby 1,2(4)










 Tylko raz.
Ale jesteś na dobrej drodze.
Tylko raz.
Ale jesteś na dobrej drodze.



 tylko ramiona w dól...
tylko ramiona w dól...


 sorry
sorry





 ?
?

 następnie skorzystać z jedynki tryg.
i doprowadzić równanie do jednej zmiennej np; sinx
następnie skorzystać z jedynki tryg.
i doprowadzić równanie do jednej zmiennej np; sinx
 ?
?
 w tym równaniu rozpatrzeć przedziałami
tylko dla x≥0 i x<0
bo 3x3 +x = x( 3x2 +1)....... dalej już wiesz
w tym równaniu rozpatrzeć przedziałami
tylko dla x≥0 i x<0
bo 3x3 +x = x( 3x2 +1)....... dalej już wiesz
 przecież rozwiązałem to wyrzej
przecież rozwiązałem to wyrzej

 x4 − 3x3 − x + 3 = 0
(x3 − 1) (x − 3) = 0
x = 1 v x = 3
a '−1' i '−3' to z tego drugiego założenia Ci wyjdzie
zgadza się?
x4 − 3x3 − x + 3 = 0
(x3 − 1) (x − 3) = 0
x = 1 v x = 3
a '−1' i '−3' to z tego drugiego założenia Ci wyjdzie
zgadza się? 
 taki wynik podałem jakieś 40 postów temu
taki wynik podałem jakieś 40 postów temu




 ale równania wole liczyć z tego że
|a|=b to
a=b lub a=−b
szybciej niż rozpatrywać na przedziały
ale równania wole liczyć z tego że
|a|=b to
a=b lub a=−b
szybciej niż rozpatrywać na przedziały


 myślałem nad czymś innym
myślałem nad czymś innym
 i (jak widać) skuteczniej
i (jak widać) skuteczniej  w ogóle skąd masz dobre wyniki przy złych
obliczeniach?
w ogóle skąd masz dobre wyniki przy złych
obliczeniach? 

 Mickej nie
rób mi tego
Mickej nie
rób mi tego  Mam nadzieję, że chociaż Klara mnie wspomoże, żeby się nie wstydzić przed
familią ubogiej listy...
Mam nadzieję, że chociaż Klara mnie wspomoże, żeby się nie wstydzić przed
familią ubogiej listy... 
 Ludzie nie akceptujcie jego zaproszeń na
naszej−klasie.pl
Ludzie nie akceptujcie jego zaproszeń na
naszej−klasie.pl
 LICZY SIE JAKOŚĆ
LICZY SIE JAKOŚĆ


 dawaj namiary daveustro
tylko jak mnie zobaczysz , to nie spadnij z fotela
dawaj namiary daveustro
tylko jak mnie zobaczysz , to nie spadnij z fotela






 Musiałaby trwać co najmniej .... 5godzin pisania
Musiałaby trwać co najmniej .... 5godzin pisania
 a wy już dzieci też się zbierajcie do łóżeczek bo późna godzinka już jest
a wy już dzieci też się zbierajcie do łóżeczek bo późna godzinka już jest
 to do zobaczenia
to do zobaczenia  Dobranoc
Dobranoc

 Rozwiązać:
x3 − 2,5x2 + 5x −2 = 0 Wiem ze trzeba skorzystac z pierwiastków wymiernych − powiedzcie po
koleji jak...
Rozwiązać:
x3 − 2,5x2 + 5x −2 = 0 Wiem ze trzeba skorzystac z pierwiastków wymiernych − powiedzcie po
koleji jak... Nigdy tego nie obiłem i dlatego nie wiem...
Nigdy tego nie obiłem i dlatego nie wiem...
 Klara wszystkich wczoraj ładnie pożegnała, to ja dzisiaj wszystkich ładnie witam
Klara wszystkich wczoraj ładnie pożegnała, to ja dzisiaj wszystkich ładnie witam  Dzień dobry!
Dzień dobry!  Tak na początek dnia:
Udowodnij, że trójkąt, w którym dwie środkowe są równej długości, jest równoramienny.
Tak na początek dnia:
Udowodnij, że trójkąt, w którym dwie środkowe są równej długości, jest równoramienny.
 . Matury nie piszę (za 5 lat), ale mogę?
. Matury nie piszę (za 5 lat), ale mogę? 
 *)
*)
 tim dawaj
tim dawaj 


 różowe − d1
czerwone − d2
niebieskie − b
czarne − c
pomarańczowe/brązowe − a
różowe − d1
czerwone − d2
niebieskie − b
czarne − c
pomarańczowe/brązowe − a
 A można to zrobić tak? :
Kolorowe kropki oznaczają odcinki równej długości.
Miedz środkowymi jest zaznaczony kąt α. Środkowe przecinają się w środku ciężkości trójkąta
który dzieli każda środkową w stosunku 2:1 a jako że środkowe mają takie same długości myślę,
że te dwa trójkąty są identyczne ( cecha bok bok kąt − coś takiego) więc jeżeli mają połowy
boków takie same to boki też są równej długości. Jak sądzicie?
A można to zrobić tak? :
Kolorowe kropki oznaczają odcinki równej długości.
Miedz środkowymi jest zaznaczony kąt α. Środkowe przecinają się w środku ciężkości trójkąta
który dzieli każda środkową w stosunku 2:1 a jako że środkowe mają takie same długości myślę,
że te dwa trójkąty są identyczne ( cecha bok bok kąt − coś takiego) więc jeżeli mają połowy
boków takie same to boki też są równej długości. Jak sądzicie?




 najpierw go źle zrozumiałem i myślałem, że trudne, a jak rzuciłem okiem na
odpowiedzi to aż się przestraszyłem, że to o to chodziło.
najpierw go źle zrozumiałem i myślałem, że trudne, a jak rzuciłem okiem na
odpowiedzi to aż się przestraszyłem, że to o to chodziło.




 a2*b2=(a*b)2 rozumiesz
a2*b2=(a*b)2 rozumiesz
 ?
?
 no tak
to daj jakieś trudne zadanko z prawdopodobieństwa
no tak
to daj jakieś trudne zadanko z prawdopodobieństwa
 Wyznacz P(A) wiedząc że P(A)*P(A')=0,25
też coś wrzućcie bo już mi się zadanka skończyły
Wyznacz P(A) wiedząc że P(A)*P(A')=0,25
też coś wrzućcie bo już mi się zadanka skończyły

 ?
?




 wtedy tylko średnia pierwiastków kwadratowego jest równa temu trzeciemu
wtedy tylko średnia pierwiastków kwadratowego jest równa temu trzeciemu 

 wystarczy że podstawił byś sobie to −2 i 2 to nie
wyjdzie ci według tego co zrobiłeś
wystarczy że podstawił byś sobie to −2 i 2 to nie
wyjdzie ci według tego co zrobiłeś
 no w tym twoim coś jest
no w tym twoim coś jest







 Zapisz w postaci ułamka ile waży cukier
5gram ile to dekagramów
Zapisz w postaci ułamka ile waży cukier
5gram ile to dekagramów


 Moge pomóc w różnych ćwiczeniach lecz jak ktoś mi pomoże
Moge pomóc w różnych ćwiczeniach lecz jak ktoś mi pomoże 
 1.Wpisz odpowiednie ułamki !
390 dni to ........ roku zwykłego
1.Wpisz odpowiednie ułamki !
390 dni to ........ roku zwykłego










 Timuś
Timuś
 '' ; **
'' ; **
 Skończę obiadek i może jakieś zadanko się dla mnie pojawi.. Hm?
Skończę obiadek i może jakieś zadanko się dla mnie pojawi.. Hm?


 390 390
−−−−− −−−−−
365 lub 366
zalezy czy przystepny czy nie!
390 390
−−−−− −−−−−
365 lub 366
zalezy czy przystepny czy nie! 
 zad: ../forum/15685
zad: ../forum/15685
 !
! 
 mam zadanie i nie umie jego rozwiązać to takie !
5
−−−−
5 =
6
−−−−
5 =
7
−−−−−
5 =
13
−−−−−−−−
5 =
18
−−−−−−
5 =
prosze odpiszcie mi
mam zadanie i nie umie jego rozwiązać to takie !
5
−−−−
5 =
6
−−−−
5 =
7
−−−−−
5 =
13
−−−−−−−−
5 =
18
−−−−−−
5 =
prosze odpiszcie mi 





 ?
?





 !
!







 rozwiąż układ równanń prostej y = x −5 i okregu x2 +y2 = 25
otrzymasz punkty: A( 5,0) i B( 0,−5)
środek S odcinka AB też wyliczysz S( 52, 52)
prosta CS jest prostopadła do prostej AB i zawiera punkty S i O
bo trójkat jest równoramienny
więc równanie prostej CS : y = −x
rozwiązując układ równań prostej SC i okregu :
otrzymasz dwa punkty C1 i C2
Z treści zad. wiesz ,że trójkąt jest ostrokatny więc już chyba będziesz wiedzieć
który punkt C przyjąć z odp:
Jeżeli chodzi o katy tego trójkata , to prosto:
skoro jest równoramiennym więc najprościej wyliczyć kąt między ramionami
czyli <ACB bo kąty przy podstawie wtedy łatwo policzysz
rozwiąż układ równanń prostej y = x −5 i okregu x2 +y2 = 25
otrzymasz punkty: A( 5,0) i B( 0,−5)
środek S odcinka AB też wyliczysz S( 52, 52)
prosta CS jest prostopadła do prostej AB i zawiera punkty S i O
bo trójkat jest równoramienny
więc równanie prostej CS : y = −x
rozwiązując układ równań prostej SC i okregu :
otrzymasz dwa punkty C1 i C2
Z treści zad. wiesz ,że trójkąt jest ostrokatny więc już chyba będziesz wiedzieć
który punkt C przyjąć z odp:
Jeżeli chodzi o katy tego trójkata , to prosto:
skoro jest równoramiennym więc najprościej wyliczyć kąt między ramionami
czyli <ACB bo kąty przy podstawie wtedy łatwo policzysz
 zad..... z ostrosłupem? ..... narysuję Ci rysunek .... i powinno pójść gładko
zad..... z ostrosłupem? ..... narysuję Ci rysunek .... i powinno pójść gładko



 ?
Pięknie rysuje
?
Pięknie rysuje


 Zad 3/ Rysuję
Zad 3/ Rysuję
 Przekrojem jest trójkat równoramienny ACD
gdzie podstawa ICAI = a i wysokością jest IDEI
ΔABW −−− jest prostokątny i równoramienny jednocześnie
więc krawędż boczna IBWI= U{a√2{2}
bo a jest przekątną kwadratu o boku IBWI
Z ΔADW prostokątnego z tw. Pitagorasa wylicz długość IADI
następnie z trójkata EAW −− prostokatnego też z tw. Pitagorasa
wylicz IDEI −−− czyli wysokość ΔCAD
podstaw do wzoru na pole
P= 12a*IDEI ...... i to wszystko
Przekrojem jest trójkat równoramienny ACD
gdzie podstawa ICAI = a i wysokością jest IDEI
ΔABW −−− jest prostokątny i równoramienny jednocześnie
więc krawędż boczna IBWI= U{a√2{2}
bo a jest przekątną kwadratu o boku IBWI
Z ΔADW prostokątnego z tw. Pitagorasa wylicz długość IADI
następnie z trójkata EAW −− prostokatnego też z tw. Pitagorasa
wylicz IDEI −−− czyli wysokość ΔCAD
podstaw do wzoru na pole
P= 12a*IDEI ...... i to wszystko Dobranoc Wszystkim
Dobranoc Wszystkim .... idę też do spanka!
.... idę też do spanka!
 ale mam problem z wyliczeniem współrzędnych C jak możesz
to proszę o pomoc
ale mam problem z wyliczeniem współrzędnych C jak możesz
to proszę o pomoc
 Jaki problem? rozwiazujesz układ równań:
y= − x i x2 +y2 = 25
to x2 + x2 = 25 => 2x2 = 25
Jaki problem? rozwiazujesz układ równań:
y= − x i x2 +y2 = 25
to x2 + x2 = 25 => 2x2 = 25

