 leży on na osi Ox, czyli ma współrzedne C(x,0), z warunku trójkąta prostokątnego mamy:
|AC|2+|BC|2=|AB|2, liczymy wszystkie długości ze wzoru https://matematykaszkolna.pl/strona/1248.html
(x+8)2+22+(x−6)2+62=142+82
x2+16x+64+4+x2−12x+36+36=196+64
2x2+4x+140=260
2x2+4x−120=0
x2+2x−60=0
policz pierwiastki i bedziesz mieć dwa rozwiązania
leży on na osi Ox, czyli ma współrzedne C(x,0), z warunku trójkąta prostokątnego mamy:
|AC|2+|BC|2=|AB|2, liczymy wszystkie długości ze wzoru https://matematykaszkolna.pl/strona/1248.html
(x+8)2+22+(x−6)2+62=142+82
x2+16x+64+4+x2−12x+36+36=196+64
2x2+4x+140=260
2x2+4x−120=0
x2+2x−60=0
policz pierwiastki i bedziesz mieć dwa rozwiązania  Chyba nigdzie nie ma błedu rachunkowego
Chyba nigdzie nie ma błedu rachunkowego

 Brak wiedzy z wektorów robi swoje − trzeba jechać z Warszawy do Łodzi przez Nowy Jork, co
zajmie tydzień, zamiast świeżo wybudowaną A2, co zajmie najwyzej 1 godzinę...
Najprościej iloczynem skalarnym wektorów − https://matematykaszkolna.pl/strona/1629.html i https://matematykaszkolna.pl/strona/1630.html .
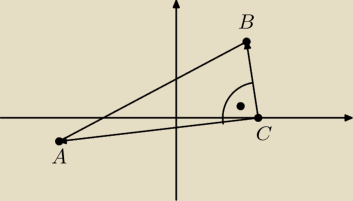
A = (−8, −2)
B = (6, 6)
C = (x, 0)
CA→=[−8−x, −2−0]=[−8−x, −2]
CB→=[6−x, 6−0]=[6−x, 6]
CA→*CB→=0 − warunek prostopadłości wektorów
CA→*CB→=(−8−x)(6−x)+(−2)*6=−48+8x−6x+x2−12=
=x2+2x−60
CA→*CB→=0 ⇔ x2+2x−60=0
Oblicz deltę, x1, x2 i otrzymasz dwa rozwiązania: C1=(x1, 0) i C2=(x2, 0)
Brak wiedzy z wektorów robi swoje − trzeba jechać z Warszawy do Łodzi przez Nowy Jork, co
zajmie tydzień, zamiast świeżo wybudowaną A2, co zajmie najwyzej 1 godzinę...
Najprościej iloczynem skalarnym wektorów − https://matematykaszkolna.pl/strona/1629.html i https://matematykaszkolna.pl/strona/1630.html .
A = (−8, −2)
B = (6, 6)
C = (x, 0)
CA→=[−8−x, −2−0]=[−8−x, −2]
CB→=[6−x, 6−0]=[6−x, 6]
CA→*CB→=0 − warunek prostopadłości wektorów
CA→*CB→=(−8−x)(6−x)+(−2)*6=−48+8x−6x+x2−12=
=x2+2x−60
CA→*CB→=0 ⇔ x2+2x−60=0
Oblicz deltę, x1, x2 i otrzymasz dwa rozwiązania: C1=(x1, 0) i C2=(x2, 0)
| −8+6 | −2+6 | |||
S=( | , | )=(−1,2) | ||
| 2 | 2 |
| −2−2√61 | ||
x1= | =1−√61 lub x2=−1+√61 | |
| 2 |