całka podwójna ania: Cześć, same całki umiem robić ale nie potrafię "ogarnąć" jak zabrać się do podwójnych. Czy ktoś na prostym przykładzie np.∫∫(x+2y)dxdy x=0 y=0 x+y=1 wytłumaczyć jak się to robi? Wiem że te 3 podane wartości to tak jakby wierzchołki trójkąta podstawy bryły której objętość liczę całkując, ale co zrobić z tym dalej? Tu na stronie niestety nie znalazłam odpowiedzi.

Bezimienny: 1. Narysuj 2. Napisz jak zmieniaja się x i y 3. Oblicz dwie całki oznaczone (iterowane)

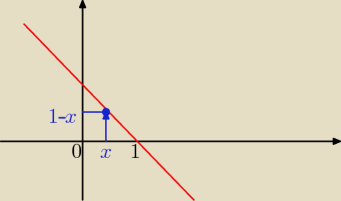
Krzysiek: zaczynasz od narysowania obszaru po którym masz całkować, potem wybierasz sobie po czym najpierw całkujesz, czy po 'x' czy po 'y' wybierzmy tak jak w przypadku całki oznaczonej pojedynczej (dygresja: jak korzystasz z tego wzoru ∫_a^b (f(x)−g(x) dx =∫_a^b (∫_g(x)^f(x) dy )dx do obliczenia pola zawartego pomiędzy funkcjami: y=f(x) , y=g(x): to tak naprawdę liczysz całkę podwójną ) po 'x' więc trzeba określić jakie funkcje 'y' ograniczają nam ten obszar, od dołu będzie to funkcja: y=0 od góry: y=1−x całkujemy po 'x' czyli: x∊[0,1] zatem całka iterowana to: ∫₀¹ (∫₀^1−x (x+2y) dy )dx

Basia: zamieniasz na całki iterowane ₀∫¹ [ ₀∫^1−x (x+2y) dy ] dx = ₀∫¹ [ xy + y² ₀|^1−x ] dx = ₀∫¹ [ x(1−x) + (1−x)² ] dx = ₀∫¹ [ x − x² + 1 − 2x + x²] dx = ₀∫¹ [−x+1] dx = [ −¹₂x² + x ] ₀|¹ = −¹₂+1 = ¹₂

Bezimienny: możesz też zapisać tak: ∫₀¹dx∫₀^1−x(x+2y)dy

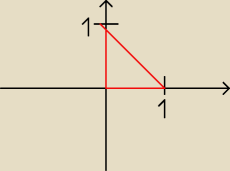
ania: x zmienia się od 0 do 1, a y to 1−x ?

Bezimienny: 0 ≤ y ≤ 1−x

Basia: właśnie tak i y zmienia się od 0 do 1−x (nie do 1 bo wtedy byłby kwadrat)

ania: dzięki, wydaje mi się że zrozumiałam, jak będę miała problemy z trudniejszymi to napiszę pozdro

Damian#UDM: A mnie zastanawia skąd w liczeniu całki w nawiasie x+2y, nie mogę tego zrozumieć

ICSP: Bo taka jest treść zadania? Jak masz zadanie: Rozwiąż równanie: x² + 5x + 4 = 0 To również pytasz dlaczego x² + 5x + 4 = 0?

Damian#UDM: No racja, pomyliłem chyba post Sorki za niedopatrzenie!

Damian#UDM: https://matematykaszkolna.pl/forum/367308.html − to miało być tutaj, lecz sprawdziłem dokładnie treść i całka tam jest taka sama, dziękuję za czujność