masakra
Humanista :):
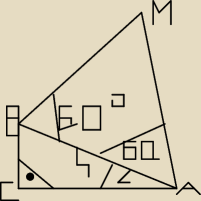
W trójkącie ABC kąt przy wierzchołku C jest prosty, przeciwprostokątna ma długość 4.
Trójkąt AMB jest równoboczny. Oblicz miary kątów ostrych trójkąta ABC, jeśli pole
trójkąta AMB jest dwa razy większe od pola trójkąta ABC.
25 kwi 12:21
dpelczar: Jesli dobrze rozumuje to:
25 kwi 12:25
tim: Mogę ja?

25 kwi 12:26
dpelczar: P
AMB = 2 * P
ABC
4
√3 = 2h
h = 2
√3
25 kwi 12:27
dpelczar: powiedz mi czy sie myle

25 kwi 12:27
dpelczar: bo teraz ma juz wszystko co mu trzeba

25 kwi 12:28
tim: Ale co to to h jest

25 kwi 12:29
dpelczar: h − wysokosc z pkt c padajaca na przeciwprostokątną − a przeciwprostokątną oznaczylem a =
4
25 kwi 12:30
tim: A obliczysz z tego kąty?

, ja to zrobiłem inaczej

25 kwi 12:31
xpt: h jest wysokością poprowadzoną na przeciwprostokątną (czyli z wierzchołka C).
Obliczenia są dobre, ale nie wiem jak to pomoże w obliczeniu zadania ;)
25 kwi 12:31
tim: No właśnie to samo myśle co xpt

25 kwi 12:31
dpelczar: kurde macie racje...

a chciałem zabłysnąć... pokarzcie jak wy to zrobiliscie

25 kwi 12:33
dpelczar: a co powiecie zeby zrobic deltoid wykorzystac dłuzsza przekątną zawierająca moje h i
jeden bok trojkąta rownobocznego

d mamy a mamy i policzymy z tego odcinek CA −...
tylko nie wiem czy dobrze mysle
25 kwi 12:37
tim: To ja

P AMB = 4
√3
a * b = 4
√3
a
2 + b
2 = 16
25 kwi 12:39
Mariusz: tak, czyli z tego co napisał Tim wynika że boki maja długość 2 i 2√3 i wszystko już
jest dane
25 kwi 12:41
tim: Potem liczysz tg, cos, sin i obliczasz dwa kąty

25 kwi 12:42
25 kwi 12:42
tim: No dawaj

25 kwi 12:44
dpelczar:
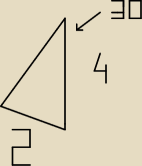
| | 1 | |
sin 30 = |
| z tego obliczylem 2   |
| | 2 | |
teraz mam h i 2 licze sin α a alfa to kąt przy wierzchołku A
25 kwi 12:46
Mariusz: ciekawe co wykombinował

25 kwi 12:46
Mariusz: ale nie wiesz czy tam jest 30
25 kwi 12:47
tim: Narysuj jak ty chcesz to h i 2 i obliczysz sin

25 kwi 12:48
tim: Mariusz: teoretycznie jak znamy boki to wiemy, gdyż jest tomtrójkąt
2280
2, 2
√3,4

25 kwi 12:48
dpelczar: albo
α = 60
0
tgα =
√3
α = 60
0
25 kwi 12:49
tim: Ok ja lece na tv

25 kwi 12:49
Mariusz: no nie wiem, jakoś nie jestem do tego przekonany, ale ok

25 kwi 12:50
dpelczar: wysokość w troj rownobocznym dzieli kąt na rowne połowy

25 kwi 12:50
dpelczar: tak mi sie wydaje − ale jesli ktos mysli ze zle to mowcie

ucze sie na błędach

25 kwi 12:51
Mariusz: no i co to nam daje, bo to to ja wiem

my musimy znaleść kąty w tym dolnym trójkącie,
więc nie możemy zakładać ile one mają bo równie dobrze mogą mieć 31 st i 59st
25 kwi 12:51
dpelczar: ja mowie ze kąt α = 60 a β=30 gdzie alfa to kąt przy wierzchołku A

25 kwi 12:53
dpelczar: ale pokarz jak ty myslisz moze ja sie myle − co sie zawsze moze zdarzyc

25 kwi 12:54
dpelczar: TIM skąd wziąłes te zależnosci


bo nie moge do tego dojsc
25 kwi 12:55
25 kwi 12:56
tim: dpelczar.. Powiedz nam powoli na rysunku, jak wyznaczyłeś, że przy A ma 30
O.

25 kwi 12:57
dpelczar: wiec
poscilem wysokosc w trojkącie rownob. i dala mi kat 300 − z rysunku wynikalo mi ze jest
to deltoid i H rownobocznego łaczyla sie z h szukanego trojkata tworzac d deltoidu
25 kwi 13:00
dpelczar: wyznaczylem ze 2 = 2

a potem to juz samo poszlo

25 kwi 13:01
dpelczar:
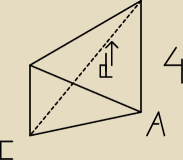
25 kwi 13:03
dpelczar: ale TIM a * b = 8
√3 a nie jak ty napisałem 4
√3 − tak mi sie wydaje

25 kwi 13:06
tim: Ale skąd wiesz, że to deltoid?

P ABM = a
2√3 / 4 = 4
√3
p ABC = a * h / 2 = 1/2 4
√3 * 2
a * h = 4
√3
25 kwi 13:17
dpelczar: teraz łąpie

w sumie masz racje

25 kwi 13:24
tim: To w końcu jest czy nie jest

[deltoid]
25 kwi 13:25
tim: Gdyby to był deltoid to:
|AB| = |AC| i kąty miałyby po 45O.
25 kwi 13:28
dpelczar: racja... kurde i tego nie wiedzalem..

a kurde matura niedlugo...
25 kwi 13:29
tim: To takie banały są, że się zapomina


25 kwi 13:30
 W trójkącie ABC kąt przy wierzchołku C jest prosty, przeciwprostokątna ma długość 4.
Trójkąt AMB jest równoboczny. Oblicz miary kątów ostrych trójkąta ABC, jeśli pole
trójkąta AMB jest dwa razy większe od pola trójkąta ABC.
W trójkącie ABC kąt przy wierzchołku C jest prosty, przeciwprostokątna ma długość 4.
Trójkąt AMB jest równoboczny. Oblicz miary kątów ostrych trójkąta ABC, jeśli pole
trójkąta AMB jest dwa razy większe od pola trójkąta ABC.




 , ja to zrobiłem inaczej
, ja to zrobiłem inaczej 

 a chciałem zabłysnąć... pokarzcie jak wy to zrobiliscie
a chciałem zabłysnąć... pokarzcie jak wy to zrobiliscie 
 d mamy a mamy i policzymy z tego odcinek CA −...
tylko nie wiem czy dobrze mysle
d mamy a mamy i policzymy z tego odcinek CA −...
tylko nie wiem czy dobrze mysle
 P AMB = 4√3
a * b = 4√3
a2 + b2 = 16
P AMB = 4√3
a * b = 4√3
a2 + b2 = 16















 ucze sie na błędach
ucze sie na błędach 
 my musimy znaleść kąty w tym dolnym trójkącie,
więc nie możemy zakładać ile one mają bo równie dobrze mogą mieć 31 st i 59st
my musimy znaleść kąty w tym dolnym trójkącie,
więc nie możemy zakładać ile one mają bo równie dobrze mogą mieć 31 st i 59st



 bo nie moge do tego dojsc
bo nie moge do tego dojsc


 a potem to juz samo poszlo
a potem to juz samo poszlo 


 P ABM = a2√3 / 4 = 4√3
p ABC = a * h / 2 = 1/2 4√3 * 2
a * h = 4√3
P ABM = a2√3 / 4 = 4√3
p ABC = a * h / 2 = 1/2 4√3 * 2
a * h = 4√3
 w sumie masz racje
w sumie masz racje 
 [deltoid]
[deltoid]
 a kurde matura niedlugo...
a kurde matura niedlugo...

