Dowody
kylo1303: Chętni na zestaw dowodów geometrycznych!
Zbieram chętnych na zestaw dowodów geometrycznych, specialnie dla nas od rumpek. Takze
wpisywac sie. Poziom dowodow: maturalny rozszerzony.
1 maj 19:19
awe: zgłaszam się

1 maj 19:20
Vax: Zgłaszam się !

1 maj 19:21
rumpek: Vax się nie liczy

[Nie jest maturzystą ]

1 maj 19:21
Vax: Eh szkoda..

1 maj 19:22
kylo1303: Ale zaliczamy go jako chetnego, takze 3ech juz jest xD
1 maj 19:22
psik: Me
1 maj 19:23
rumpek: Ok, za 30 minut coś wrzucę, wpierw znajdę

1 maj 19:24
kylo1303: rumepk Jasne, wszyscy beda wdzieczni

1 maj 19:31
loko: poproszem
1 maj 19:31
Eta:
Ja też poproszę


1 maj 19:52
Natalia: I ja!
1 maj 19:56
koło: ja również poprosze

1 maj 19:59
emagnuski: I too
1 maj 20:00
rumpek:
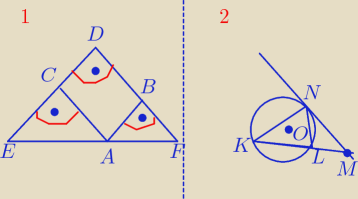 Zakres rozszerzony
Zakres rozszerzony − typowo maturalne
Zadanie 1 (3pkt)
Mając podany trapez ABCD, oraz punkt S, który jest środkiem jednego z ramion danego czworokąta.
Dany punkt połączono z wierzchołkami drugiego ramienia. Udowodnij, że pole danego trójkąta
jest dokładnie połową pola trapezu.
Zadanie 2 (3pkt)
W trójkącie ABC dana jest prosta y, która jest równoległa względem podstawy. Dana prosta
przecina się z bokami odpowiednio w punktach E i F. Pole powstałego trapezu jest równe polu
| | |CE| | |
powstałego trójkąta [mniejszego]. Uzasadnij, że zachodzi: |
| = √2 + 1. [ |AB| − |
| | |EA| | |
podstawa, |AC| i |BC| ramiona tego trójkąta]. Zadanie pisałem z pamięci, chyba dobrze
 Zadanie 3 (4pkt)
Zadanie 3 (4pkt)
Dany jest trapez od podstawach odpowiednio x i . Przekątne tego trapezu przecinają się w
punkcie O, przez ten punkt prowadzimy prostą równoległą do podstaw. Dana prosta równoległa
przecina się z ramionami odpowiednio w punktach: E i F. Uzasadnij, że odcinek |EF| jest równy
| | 2xy | |
|
| . [średnia harmoniczna] |
| | x + y | |
Zadanie 4 (4pkt)
Na rysunku [rysunek 1] mamy przedstawione: trójkąt równoramienny △DEF. Z wierzchołka A będącego
na przeciwprostokątnej |EF| poprowadzono odcinki |AC| i |AB|, są one prostopadłe odpowiednio
do boków |DF| i |DE|. Wykaż, że |AC| + |AB| = |EF|.
Zadanie 5 (4pkt)
W trapezie o podstawach a,b (a,b > 0). Wykaż, że długość odcinka łączącego środki przekątnych
Zadanie 6 (4pkt)
Uzasadnij, że dla trójkąta △ABC iloczyn długości dwóch jego boków jest równy 2hR (h − wysokość
padająca na trzeci bok) R − promień okręgu opisanego na trójkącie ABC.
Zadanie 7 (3pkt)
Patrząc na rysunek [rysunek 2] i wiedząc, że |LM| = |LN| udowodnij, że zachodzi związek |KN| =
|NM|.
Zadanie 8 (4pkt)
Na bokach AC i BC trójkąta ABC obrano punkty P i Q takie, że |AP| : |PC| = 2 :1 oraz |BQ| :
|QC| = 2 :1. Odcinki AQ i BP przecinają się w punkcie R . Wykaż, że pole czworokąta CP RQ jest
równe polu trójkąta ARP .
Zadanie 9 (2pkt)
Na przekątnej równoległoboku ABCD [przekątna BD] wybierz dowolny punkt M. Uzasadnij, że pole
trójkątów AMD oraz CDM są takie same.
Zadanie 10 (3pkt)
| | a + b − c | |
Udowodnij, że dla trójkąta prostokątnego długość promienia jest równa |
| . |
| | 2 | |
Zadanie 11 (4pkt)
W trapezie ABCD o podstawach a i b (a> b) na przedłużeniu odcinka DC zaznaczono punkt x tak,że
prosta |AX| podzieliła ten trapez na dwie części o równych polach. Wykaż, że odcinek |CX| =
Wszystkie zadania typowo maturalne

Łatwy poziom.
1 maj 20:08
rumpek: Eta no bez "jaj"


1 maj 20:08
Eta:
No dobrze

pasuję, bo to banalne

Powodzenia Wszystkim zainteresowanym


1 maj 20:13
kylo1303: Ide cos przejem a potem trzeba sie bedzie brac do roboty. Dzieki wielkie


1 maj 20:17
blogther: w zadaniu 10 długosc promienia opisanego czy wpisanego?
1 maj 20:25
Vax: Wpisanego.
1 maj 20:27
blogther: czy to z polecenia mamy sie domyslic ze promien lezy na boku tego trojkata
chyba to jednak tak bedzie
1 maj 20:27
rumpek: Wpisanego naturalnie

1 maj 20:27
blogther: w zadaniu drugim tez cos ucieło
1 maj 20:29
blogther: nie okey wszysto dobrze jestw tym zad 2
1 maj 20:30
problematyk: Jak najlepiej uczyc sie dowodow? Tzn. jakas ksiazka/strona , samemu probowac czy gotowe
analizowac ? Bo kompletnie mi to nie idzie

Z tych dowodow to z 5−6 bym zrobil, w tym 4
pamietam na pamiec

1 maj 20:30
blogther: ten trapez z zadania pierwszego to jest dowolny czy moze byc prostokatny rownoramienny
bo tam pisze ze jest podany ten trapez
1 maj 20:36
awe: dzięki wielkie
rumpek! pierwsze już zrobiłam, zaraz rozkminiam następne

1 maj 20:45
pawe:
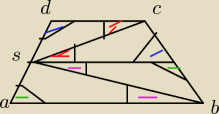
zadanie 1
pokazałem, że trapez dzieli się na 2 częśći, i te 2 częśći dzielą się na połowy, zaznaczyłem
kolorami te same kąty
czy taki dowód wystarczy?
1 maj 21:02
pawe: sorry, zadanie jest całkowicie źle, coś pomieszałem xD to moje 1
1 maj 21:05
kylo1303:
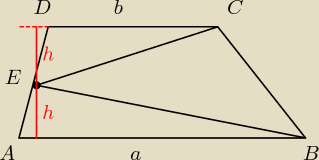
Jako ze punkt E jest polowa ramienia, wiec odcinki prostopadle do odpowiednich podstaw sa rowne
(jak ktos nie wierzy to niech pokaze to z podobienstwa trojkatow

).
| | 1 | |
PABCD= |
| *2h*(a+b)=h*(a+b)
|
| | 2 | |
| | 1 | | 1 | |
PΔCDE+PΔABE= |
| *h*(a+b)= |
| *PABCD
|
| | 2 | | 2 | |
| | 1 | | 1 | |
PΔBCE=PABCD− (PΔCDE+PΔABE)=PABCD − |
| *PABCD = |
| *PABCD c.n.u |
| | 2 | | 2 | |
1 maj 21:18
kylo1303: Zadanie 2:
Pc=2P
1
| PΔEFC | | P1 | | 1 | | √2 | |
| = |
| = |
| =k2 → k= |
|
|
| PΔABC | | 2P1 | | 2 | | 2 | |
Dalej ladnie wyjdzie.
Poki co te 2 zadania malo ambitne.
1 maj 21:25
rumpek: Zrób do zadania 2 rysunek, i dokończ.
1 maj 21:26
Dociekliwy: To ja zapytam skąd te zadania, bo szczerze mówiąc niektóre już widziałem i nie pamiętam gdzie
xD
1 maj 21:30
kylo1303:
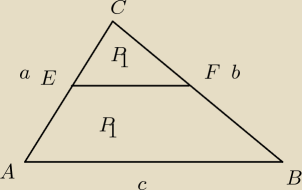
Rysunek troche nie odzwierciedla rzeczywistosci ale to bez znaczenia
|AC|=a
|BC|=b
|AB|=c
P
ABC=P
ABFE+P
EFC=2P
1
wyzej policzylem ze:
| |CE| | | | | √2 | | √2*(2+√2) | |
| = |
| = |
| = |
| |
| |EA| | | | | 2−√2 | | (2−√2)*(2+√2) | |
Prosze tato

1 maj 21:34
rumpek: 
2 pierwsze zadania z OE

podstawa

1 maj 21:36
kacper: podstawa rozszerzenia

1 maj 21:37
kylo1303: No to sie podbudowalem, zadania z podstawy nie stanowia dla mnie wiekszego
problemu <jupiii> To teraz za trzecie, po tresci wyglada trudniej.
1 maj 21:39
rumpek: 

1 maj 21:39
kylo1303: Zadanie 3 chwilowo odpuszczam bo widze tam mase podobienstwa trojkatow, a nei chce mi sie
wprowadzac tylu rownan juz na samym poczatku rozwiazywania, takze zaczalem 4.
Zadanie 4.
|EA| jest przeciwprostokatna w ΔEAC ⇒ |EA|>|AC|
|AF| jest przeciwprostokatna w ΔAFB ⇒ |AF|>|AB|
|EA|+|AF|>|AC|+|AB|
|EF|>|AC|+|AB|
Czyli rownosc |EF|=|AC|+|AB| nie zachodzi.
1 maj 21:49
kylo1303:
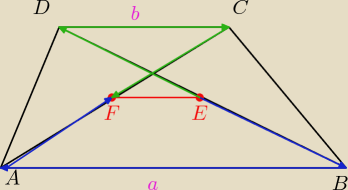
I tutaj mam problem bo nie wiem jak zapisac wektory, dlatego bede pisal w nawiasie kwadratowym
( [] ).
[EB]=−[ED]
[AF]=−[CF]
|CD|=b
|AB|=a
[EF]=[EB]+[BA]+[AF]
[EF]=[ED]+[DC]+[CF]
+ −−−−−−−−−−−−−−−−−−−−−−−−−−−−−
2[EF]=[EB]+[BA]+[AF]+[ED]+[DC]+[CF]
2[EF]=[BA]+[DC]+[EB]−[EB]+[AF]−[AF]
2[EF]=[BA]+[DC] −> zmieniam wektor [DC] na [CD]
2[EF]=[BA]−[CD]
1 maj 22:01
rumpek:
Zadanie 5 Znacznie krócej

Nie rób tego wektorowo
 Zadanie 4
Zadanie 4 No przecież sam napisałeś |EA| > |AC| ∧ |AF| > |AB| (bo przeciwprostokątne są
dłuższe) Sumując to przecież otrzymasz prawdę

1 maj 22:07
kylo1303:
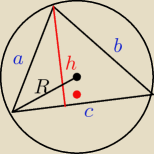
2Rhc=abc /:c (bo c>0)
2Rh=ab c.n.u
1 maj 22:08
kylo1303: W zadaniu 4 zatem jest blad w poleceniu, dales tam "=". To zadanie 5 kiedys robilem i to
wlasnie na 2 sposoby, zaraz zrobie nie−wektorowo.
1 maj 22:09
rumpek: Zadanie 6 można również dobrze z tw. sinusów i przede wszystkim ten pomysł był punktowany

1 maj 22:09
rumpek: kylo1303 no ale o co chodzi? Ty napisałeś nierówność która jest prawdziwa, nie wiem po co
ale ok. A masz udowodnić przecież
|AC| + |AB| = |EF| 
1 maj 22:10
kylo1303: | | abc | |
Na dobra sprawe to wzor |
| bierze sie z tw. sinusow takze moznaby rzec ze na jedno |
| | 4R | |
wychodzi.
1 maj 22:10
kylo1303: Hmmm... albo ja czegos nie lapie albo nie wiem. Skoro mam udowodnic ze |AC| + |AB| = |EF|, a
pokazalem ze |EF| jest wiekszy od |AC|+|AB| czyli pokazalem ze teza jest nieprawdziwa.
1 maj 22:12
rumpek: ajajajaj, dobra, moja wina
 |AC| + |AB| = |ED|
|AC| + |AB| = |ED| 
Sorki

Alfabet mi się pomieszał

1 maj 22:14
kylo1303: Dobra, to wracamy do zadania 4 a po nim bedzie zadanie 5.
1 maj 22:19
kylo1303:
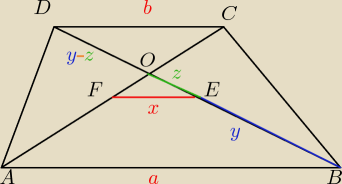
Z podobienstwa trojkatow:
oraz
az=xy+xz
bz=xy−xz
xy=az−xz
xy=bz+xz
bz+xz=az−xz
2xz=az−bz
2x=a−b
1 maj 22:29
Eta:
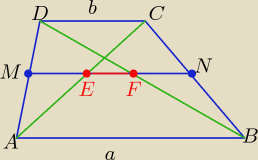
@
kylo1303
środkowa MN trapezu zawiera odcinek
EF
z podobieństwa trójkątów ACD i AEM
| | a+b | | a−b | |
|EF|= |MN| −b = |
| −b= |
| |
| | 2 | | 2 | |
c.n.u


1 maj 22:42
rumpek:
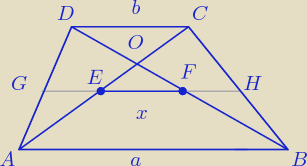
| | 1 | | 1 | |
|AG| = |
| |AD| i |BH| = |
| |CB| |
| | 2 | | 2 | |
z tw. Talesa dla trójkątów: △ADC i △ABD otrzymujemy:
| | 1 | | 1 | |
|EG| = |
| b i |FG| = |
| a |
| | 2 | | 2 | |
| | 1 | | 1 | | a − b | |
x = |FG| − |EG| = |
| a − |
| b = |
| |
| | 2 | | 2 | | 2 | |
c.n.u.

1 maj 22:42
rumpek: jasny gwint


1 maj 22:43
Eta:

1 maj 22:43
Maslanek: Z. 10
Okręgu jakiego?
1 maj 22:44
Eta:
Dorzucę takie zadanie

| | 1 | | 2 | | 4 | |
Rozwiąż równanie: x3+2x2+4x+ |
| + |
| + |
| = 44 |
| | x3 | | x2 | | x | |
1 maj 22:50
kylo1303: Hmm... no nie da sie ukryc ze wasz sposob krotszy. W ogole przeoczylem ze to polowa
boku xD Chwilowo robie sobie przerwe ale dzisiaj postaram sie wrzucic jeszcze ze 2−3 dowody,
wszystkich raczej nei zrobie bo planuje napisac esej z angielskiego zeby miec material do
opracowywania.
1 maj 22:51
rumpek: Eta 
zadania "wykaż, że geometryczne"

1 maj 22:51
Eta:
Oj tam, oj tam

1 maj 22:52
Maslanek: | | 1 | | 1 | | 1 | |
x3 + |
| + 2(x2 + |
| ) + 4(x+ |
| ) = |
| | x3 | | x2 | | x | |
| | 1 | | 1 | | 1 | | 1 | |
= (x+ |
| ) (x2 − 1 + |
| ) + 2((x+ |
| )2 − 2) + 4(x+ |
| ) = |
| | x | | x2 | | x | | x | |
| | 1 | | 1 | | 2 | |
= (x+ |
| ) (x2 − 1 + |
| + 2x + |
| − 4 + 4) = |
| | x | | x2 | | x | |
| | 1 | | 1 | | 1 | |
= (x+ |
| ) ((x+ |
| )2 − 2 + 2(x+ |
| ) − 1) = |
| | x | | x | | x | |
Niech t =x+1/x
t (t
2 − 2 + 2t −1) =44
t
3 + 2t
2 − 3t − 44 = 0
Dobrze póki co?
Gdzieś błąd jest, bo nie wychodzą mi pierwiastki wymierne

1 maj 23:01
Maslanek: Dobra...
Już wiem gdzie

t
3 − 3t + 2t
2 − 4 + 4t =44
t
3 + 2t
2 + t − 48 = 0
t=3.
Dalej (t−3)(t
2+5t+16) = 0
t=3
x
2 − 3x + 1 = 0
1 maj 23:06
Eta:
| | 1 | | 1 | | 1 | |
x+ |
| =t x2+ |
| = t2−2 x3+ |
| = t3−3t |
| | x | | x2 | | x3 | |
t
3−3t+2(t
2−2)+4t−4=44
1 maj 23:10
Eta:


1 maj 23:11
Maslanek: Jedno −4 za dużo na końcu Eta

1 maj 23:12
Maslanek: 

1 maj 23:12
1 maj 23:12
Eta:
Faktycznie

1 maj 23:13
Maslanek: Ja jabłek za darmo nie rozdaję

1 maj 23:14
rumpek: Ecie jabłko "żydzisz"

?
1 maj 23:21
Maslanek: Oj, oj. Etmafia

1 maj 23:22
kylo1303:
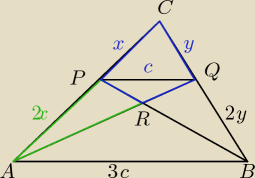
Sry za przestoj ale mialem przerwe, ale widze ze bede potrzebowal jej wiecej. Robilem zadanie 8
i dowodzilem ze czworokat jest rowny ABR a nie APR... jak nietrudno zgadnac nie chcialo mi
wyjsc. W kazdym badz razie rozwiazanie:
Zadanie 8
W trojkatach ABR i RQB wysokosc jest taka sama.
| AR | | 1 | | PRQB | | 1 | |
| = |
| → |
| = |
|
|
| RQ | | 3 | | PABR | | 3 | |
P
APR=P
RBQ (wspolna podstawa i wysokosc i potem odjac PRQ− nie chce mi sie pisac i
dowodzic oddzielnie)
P
PQR=P
1
| | 8 | |
PABQP=P1 + 3P1 + 3P1 + 9P1= 16P1 = |
| PABC
|
| | 9 | |
| | 1 | | 1 | | 1 | |
PPRQC=( |
| + |
| ) * PABC= |
| PABC
|
| | 9 | | 18 | | 6 | |
Ehh.. Masakra. Pisanie tego zajelo mi chyba z 20minut, nie wiem nawet czy to logiczne jest.
Teraz to chyba bede pisal tylko sposob rozwiazania bo cos takiego to nie na moje sily. +
pewnie dalo sie 100 razy krocej, ale w zeszycie jak wprowadzilem ladne oznaczenia to duzo duzo
krocej zajelo.
1 maj 23:29
psik:
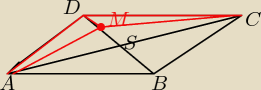
No więc Trójkąty te mają wspólny bok |DM|. Wprowadzę pewne kąty:
∡DSC = β , ∡DSA = 180
o − β
Policzę te pola następująco:
P
ΔAMD = P
ΔASD − P
ΔASM
P
ΔDMC = P
ΔDSC − P
ΔCSM
| | 1 | |
PΔASD = |
| |AS|*|DS|*sin(180o − β) |
| | 2 | |
| | 1 | |
PΔDSC = |
| |DS|*|SC|*sinβ |
| | 2 | |
| | 1 | |
PΔASM = |
| |AS|*|DM|*sin(180o − β) |
| | 2 | |
| | 1 | |
PΔCSM = |
| |DM|*|SC|*sinβ |
| | 2 | |
| | 1 | | 1 | |
PΔAMD = PΔASD − PΔASM = |
| |AS|*|DS|*sin(180o − β) − |
| |AS|*|DM|*sin(180o |
| | 2 | | 2 | |
− β)
z wzorów redukcyjnych : sin(180
o − β) = sinβ, bo sinus kąta w trójkącie zawsze jest dodatni.
| 1 | | 1 | |
| |AS|*|DS|*sinβ − |
| |AS|*|DM|*sinβ |
| 2 | | 2 | |
| | 1 | | 1 | |
PΔDMC = PΔDSC − PΔCSM = |
| |DS|*|SC|*sinβ − |
| |DM|*|SC|*sinβ |
| | 2 | | 2 | |
| | 1 | |
a ponieważ |AS| = |SC| = |
| |AC| ( połowa przekątnej ) to otrzymaliśmy dokładnie taki sam |
| | 2 | |
wzór na pole obu trójkątów, czyli P
ΔDMC = P
ΔAMD , c.n.u. Uff
1 maj 23:30
psik: Kylo ty chociaż zad. za 4 pkt. Ja robiłem zad. 9, za 2

1 maj 23:32
kylo1303: Heh, dla mnie to niewielka roznica. Ale skoro za 2pkt to pewnie dalo sie krocej. Normalnie to
mi w miare sprawnie idzie to pisanie, ale ostatnio zauwazylem ze wieczorami mozg wysiada. Przy
czym kiedys bylo calkiem inaczej, wieczorkiem dopiero siadalem do roboty. Mysle ze wynika to z
tego ze teraz w dzien cos robie, a kiedys to po calym dniu leniuchowania mozg byl wypoczety.
Ja to na dzisiaj pasuje z dowodami, jutro zajme sie reszta.
1 maj 23:37
psik: W 9 można też było wykazać przystawanie trójkątów ale nie wiem jak

1 maj 23:44
rumpek:
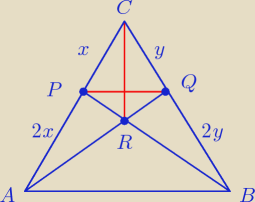 Zadanie 8
Zadanie 8
T: P
CPRQ = P
ARP
* P
ARP = 2P
CRR
(mają tę samą wysokość opuszczoną na podstawę oraz podstawy są w stosunkach 2 : 1)
** P
BRQ = 2P
CQR
(mają tę samą wysokość opuszczoną na podstawę oraz podstawy są w stosunkach 2 : 1)
| | 1 | | 1 | |
PCPRQ = PCPR + PCQR = |
| PARP + |
| PBRQ |
| | 2 | | 2 | |
Pozostało udowodnić tylko, że P
△ARP = P
△BRQ, nie jest to trudne, ponieważ:
Rozpatrzmy trójkąty: △ABQ i △ABP mają one równą podstawę i tę samą wysokość, zatem są równe:
P
△ABQ = P
△ABP ⇒ P
△ARP + P
△ARB = P
△BRQ + P
△ABR ⇒
P△ARP = P△BRQ
| | 1 | | 1 | |
Zatem: PCPRQ = |
| P△ARP + |
| P△ARP = P△ARP |
| | 2 | | 2 | |
c.n.u.

1 maj 23:47
psik: A jak z 9?
1 maj 23:50
rumpek:
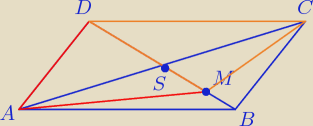 psik
psik u Ciebie? A co jeśli punkt będzie leżał poza punktem S? Tak jak w tym wypadku

?
2 maj 00:02
Henio:
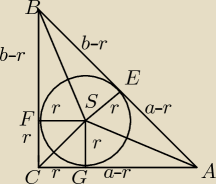
zadanie 10
△ASG jest przystający △AES bkb
△CGS jest przystający △CSF bkb
△FSB jest przystający △SEB bkb
więc
c=a−r+b−r
−2r=c−a−b
2r=a+b−c
2 maj 09:53
Daniel: zadanie 10.
podstawa ?
2 maj 10:11
Henio: podstawa to a
przyprostokątna z lewej to b
przeciwprostokątna to c
2 maj 10:38
Daniel: się pytałem o poziom

, bo dziecinnie proste

2 maj 10:45
rumpek: Zadanie 1,2, 10 to poziom podstawowy, reszta była brana z rozszerzonego. Napisałem, że zadania
typowo maturalne − najlepsze 3, 11, 8 (już zrobiłem).
2 maj 10:50
Daniel: a ja walcze z tym 11

, czuje ze zaraz wyjdzie
2 maj 10:52
Eta:
Zostało jeszcze parę zadań do rozwiązania!

2 maj 20:05
kylo1303: To dobrze, czekaja na mnie

Ale to dopiero wieczorem, tj za 1−2h. Najwazniejsze mecze
ligi hiszpanskiej sie zaczely wiec zadania musza poczekac.
2 maj 20:19
rumpek: Te najciekawsze nie zostały ruszone

Dobra idę na film "Wieczny student"

2 maj 20:36
Maslanek: A co zostało?

2 maj 20:41
kylo1303: Tzn jesli chodzi o mnie to zostaly mi jeszcze 3,4,9,10,11. Postaram sie dzisiaj zrobic.
2 maj 21:10
kylo1303: Kurde... w zadaniu 11 wyszlo mi cos takiego:
| | a*(−b) | |
|CX|= |
| czyli gdzies mi ucieklo jedno "a"  Zaraz sprobujemy znalezc blad. |
| | a+b | |
2 maj 21:34
kylo1303: Dobra, Zadanie 11 is done.
2 maj 21:51
kylo1303: 10 i 9 tez poszlo, jeszcze tylko 3 i 4.
2 maj 22:03
kylo1303: Ehh.. juz widze czemu mialem problemuy z 4 wczoraj. W zadaniu nie ma wspomniane ze to
trojkat prostokatny, dopeiro teraz na rysunku zauwazylem. Przydaloby sie takie informacje w
tresci dawac

2 maj 22:06
kylo1303: W sumie to jesy "przeciwprostokatna" ale chyba musialem to uznac za blad czy cos

To teraz pewnie bez wiekszych problemow pojdzie.
Sry ze pisze post pod postem xD
2 maj 22:08
kylo1303: Zadanie 4 is done. Zostalo jeszcze jedynie zadanie 3. Gdyby ktos chcial rozwiazanie to
moge napisac, ale tak o wszystkich to nie chce mi sie tracic czasu i zdrowia na wklepywanie
formulek.
2 maj 22:09
kylo1303: rumpek Zrobiles zadanie 3?
3 maj 14:54
rumpek: Jakbym nie zrobił to bym go nie dał

3 maj 15:14
kylo1303: W zadaniu sporo mozna zdzialac z podobienstwa trojkatow, ale brakuje mi chyba jednego
rownania czy czegos. I tutaj wlasnie sie zaczalem zastanawiac czy przypadkiem punkt przeciecia
przekatnych nie dzieli tego boku na polowy. Wydaje mi sie ze tak jest ale nie mam pewnosci

W kazdym badz razie jak ci sie zechce to mozesz napisac rozwiazanie xD
3 maj 15:19
rumpek: Koło 18 − 19 napisze

teraz powtarzam polski <

>
3 maj 15:23
kylo1303: Jakby co to czekam na dowod, przy czym nie pospieszam− tylko przypominam xD
4 maj 15:28
Godzio:
Zadanie 3 ?
5 maj 19:32
5 maj 19:36
kylo1303: Ano zadanie 3. Nawet udalo mi sie udowodnic ze EO i FO sa sobie rowne

5 maj 19:37
Godzio:
To robię, ciekawe czy wyjdzie

5 maj 19:38
kylo1303: Tak na dobra sprawe to mi wyszlo, ale dopiero po przeczytaniu rozwiazania (tzn przeczytalem
jak ktos robil i wtedy sam ponownie podszedlem do zadania, znajac sposob wykazalem) xD
Ale chce wiedziec czy jest inny sposob, moze latwiejszy.
5 maj 19:45
Godzio:
| y | | h | |
| = |
| , h = h1 + h2 (to wysokości trójkątów na jakie dzielą przekątne trapez) |
| EO | | h2 | |
| y | | h1 | | h1 | | y | |
| = |
| + 1, ale z podobieństwa wiemy, że |
| = |
| |
| EO | | h2 | | h2 | | x | |
| | xy | |
EO = |
| , ponieważ EO = OF to długość szukane odcinka to: |
| | y + x | |
A to, że EO = OF już sobie udowodniłeś, więc dowodu nie pisze

5 maj 20:01
kylo1303: Juz widze ze krotszy, zaraz przeanalizuje i moge podac "swoje rozwiazanie" (nie tak znowu
moje, ale powiedzmy ze po prostu inne)
5 maj 20:03
kylo1303: W sumie to zasada rozwiazywania podobna, tylko w moim nie korzystalem z wysokosci tylko z bokow
i troche wiecej zamieniania bylo. Ale tez trzeba bylo "rozlozyc" dlugi bok na sume dwoch i
rozwiazac. Dzieki wielkie
Godziu 
5 maj 20:19
rumpek: Jest git


Można inaczej: zauważyć, że trójkąty są podobne wyznaczamy h w zależności:
h = h
1 + h
2 i porównujemy pola

5 maj 20:20
letarg: Mógłby ktoś podrzucić jakąś wskazówkę do 11

? Męczę się z tym już kupę czasu i nadal nic...
6 maj 18:00
Kacper:

29 sie 18:01
daras: gdzie są chłopcy z tamtych lat

jasne kwiaty

29 sie 18:04
Dziadek Mróz:
Kąt prosty jest prosty bo ma 90o. Serio
29 sie 18:11
:): Inne kąty są już nieco trudniejsze?
29 sie 18:16
Janek191:

29 sie 19:04
Eta:
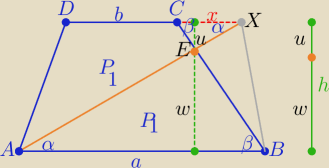
Zad.11/ ( treść zadania wyżej podana przez
rumpek
| | a(a−b) | |
Mamy wykazać,że |CX|=x= |
| |
| | a+b | |
Dowód:
| | a+b | |
P(trapezu)=2P1 ⇒ 2P1= |
| *h ⇒ 4P1=(a+b)(w+u) |
| | 2 | |
Trójkąty ABE i CEX są podobne z cechy (kkk) to:
P(ABE)= P
1 ⇒ 2P
1=a*w to 4P
1=2aw
zatem: 2aw=(a+b)(w+u) ⇒ aw−bw=au+bu ⇒ (a−b)w=(a+b)u
| | w | | a+b | | a | | a+b | | a(a−b) | |
to |
| = |
| ⇒ |
| = |
| ⇒ |CX|= x= |
| |
| | u | | a−b | | x | | a−b | | a+b | |
c.n.w.
30 sie 13:53
daras: η jesteś niezawodna ! Kacper odgrzebał link sprzed 3 lat

30 sie 13:58
30 sie 14:08
Eta:
I dobrze,że "wykopał" to zadanie , bo nie zostało do tej pory rozwiązane

30 sie 14:10
Kacper:
Ja je znalazłem przypadkiem jak szukałem zadań z geometrii
 Eta
Eta 
Wakacje na mnie źle działają

zapominam wiele ciekawych rzeczy i proste zadania stają się
trudne

30 sie 14:13
daras: η o co Ty mnie ciągle podejrzewasz ?
to piękna piosenka Marleny Dietrich, spolszczona przez Sławę Przybylską− znasz ?

30 sie 14:16
daras: ja nie miałem wakacji więc nadal proste zadania rozwiązuję w pamięci, byle nie geometryczne
bo tutaj nie umiem rysować

30 sie 14:18
Eta: 
30 sie 18:31


 [Nie jest maturzystą ]
[Nie jest maturzystą ] 






 Zakres rozszerzony − typowo maturalne
Zadanie 1 (3pkt)
Mając podany trapez ABCD, oraz punkt S, który jest środkiem jednego z ramion danego czworokąta.
Dany punkt połączono z wierzchołkami drugiego ramienia. Udowodnij, że pole danego trójkąta
jest dokładnie połową pola trapezu.
Zadanie 2 (3pkt)
W trójkącie ABC dana jest prosta y, która jest równoległa względem podstawy. Dana prosta
przecina się z bokami odpowiednio w punktach E i F. Pole powstałego trapezu jest równe polu
Zakres rozszerzony − typowo maturalne
Zadanie 1 (3pkt)
Mając podany trapez ABCD, oraz punkt S, który jest środkiem jednego z ramion danego czworokąta.
Dany punkt połączono z wierzchołkami drugiego ramienia. Udowodnij, że pole danego trójkąta
jest dokładnie połową pola trapezu.
Zadanie 2 (3pkt)
W trójkącie ABC dana jest prosta y, która jest równoległa względem podstawy. Dana prosta
przecina się z bokami odpowiednio w punktach E i F. Pole powstałego trapezu jest równe polu
 Zadanie 3 (4pkt)
Dany jest trapez od podstawach odpowiednio x i . Przekątne tego trapezu przecinają się w
punkcie O, przez ten punkt prowadzimy prostą równoległą do podstaw. Dana prosta równoległa
przecina się z ramionami odpowiednio w punktach: E i F. Uzasadnij, że odcinek |EF| jest równy
Zadanie 3 (4pkt)
Dany jest trapez od podstawach odpowiednio x i . Przekątne tego trapezu przecinają się w
punkcie O, przez ten punkt prowadzimy prostą równoległą do podstaw. Dana prosta równoległa
przecina się z ramionami odpowiednio w punktach: E i F. Uzasadnij, że odcinek |EF| jest równy
 Łatwy poziom.
Łatwy poziom.


 pasuję, bo to banalne
pasuję, bo to banalne  Powodzenia Wszystkim zainteresowanym
Powodzenia Wszystkim zainteresowanym 




 Z tych dowodow to z 5−6 bym zrobil, w tym 4
pamietam na pamiec
Z tych dowodow to z 5−6 bym zrobil, w tym 4
pamietam na pamiec 

 zadanie 1
pokazałem, że trapez dzieli się na 2 częśći, i te 2 częśći dzielą się na połowy, zaznaczyłem
kolorami te same kąty
czy taki dowód wystarczy?
zadanie 1
pokazałem, że trapez dzieli się na 2 częśći, i te 2 częśći dzielą się na połowy, zaznaczyłem
kolorami te same kąty
czy taki dowód wystarczy?
 Jako ze punkt E jest polowa ramienia, wiec odcinki prostopadle do odpowiednich podstaw sa rowne
(jak ktos nie wierzy to niech pokaze to z podobienstwa trojkatow
Jako ze punkt E jest polowa ramienia, wiec odcinki prostopadle do odpowiednich podstaw sa rowne
(jak ktos nie wierzy to niech pokaze to z podobienstwa trojkatow  ).
).
 Rysunek troche nie odzwierciedla rzeczywistosci ale to bez znaczenia
|AC|=a
|BC|=b
|AB|=c
PABC=PABFE+PEFC=2P1
wyzej policzylem ze:
Rysunek troche nie odzwierciedla rzeczywistosci ale to bez znaczenia
|AC|=a
|BC|=b
|AB|=c
PABC=PABFE+PEFC=2P1
wyzej policzylem ze:

 2 pierwsze zadania z OE
2 pierwsze zadania z OE  podstawa
podstawa 



 I tutaj mam problem bo nie wiem jak zapisac wektory, dlatego bede pisal w nawiasie kwadratowym
( [] ).
[EB]=−[ED]
[AF]=−[CF]
|CD|=b
|AB|=a
[EF]=[EB]+[BA]+[AF]
[EF]=[ED]+[DC]+[CF]
+ −−−−−−−−−−−−−−−−−−−−−−−−−−−−−
2[EF]=[EB]+[BA]+[AF]+[ED]+[DC]+[CF]
2[EF]=[BA]+[DC]+[EB]−[EB]+[AF]−[AF]
2[EF]=[BA]+[DC] −> zmieniam wektor [DC] na [CD]
2[EF]=[BA]−[CD]
I tutaj mam problem bo nie wiem jak zapisac wektory, dlatego bede pisal w nawiasie kwadratowym
( [] ).
[EB]=−[ED]
[AF]=−[CF]
|CD|=b
|AB|=a
[EF]=[EB]+[BA]+[AF]
[EF]=[ED]+[DC]+[CF]
+ −−−−−−−−−−−−−−−−−−−−−−−−−−−−−
2[EF]=[EB]+[BA]+[AF]+[ED]+[DC]+[CF]
2[EF]=[BA]+[DC]+[EB]−[EB]+[AF]−[AF]
2[EF]=[BA]+[DC] −> zmieniam wektor [DC] na [CD]
2[EF]=[BA]−[CD]
 Nie rób tego wektorowo
Nie rób tego wektorowo  Zadanie 4 No przecież sam napisałeś |EA| > |AC| ∧ |AF| > |AB| (bo przeciwprostokątne są
dłuższe) Sumując to przecież otrzymasz prawdę
Zadanie 4 No przecież sam napisałeś |EA| > |AC| ∧ |AF| > |AB| (bo przeciwprostokątne są
dłuższe) Sumując to przecież otrzymasz prawdę 



 |AC| + |AB| = |ED|
|AC| + |AB| = |ED|  Sorki
Sorki  Alfabet mi się pomieszał
Alfabet mi się pomieszał 
 Z podobienstwa trojkatow:
Z podobienstwa trojkatow:
 @ kylo1303
środkowa MN trapezu zawiera odcinek EF
z podobieństwa trójkątów ACD i AEM
@ kylo1303
środkowa MN trapezu zawiera odcinek EF
z podobieństwa trójkątów ACD i AEM








 zadania "wykaż, że geometryczne"
zadania "wykaż, że geometryczne" 


 t3 − 3t + 2t2 − 4 + 4t =44
t3 + 2t2 + t − 48 = 0
t=3.
Dalej (t−3)(t2+5t+16) = 0
t=3
t3 − 3t + 2t2 − 4 + 4t =44
t3 + 2t2 + t − 48 = 0
t=3.
Dalej (t−3)(t2+5t+16) = 0
t=3





 https://matematykaszkolna.pl/forum/144150.html
https://matematykaszkolna.pl/forum/144150.html


 ?
?

 Sry za przestoj ale mialem przerwe, ale widze ze bede potrzebowal jej wiecej. Robilem zadanie 8
i dowodzilem ze czworokat jest rowny ABR a nie APR... jak nietrudno zgadnac nie chcialo mi
wyjsc. W kazdym badz razie rozwiazanie:
Zadanie 8
Sry za przestoj ale mialem przerwe, ale widze ze bede potrzebowal jej wiecej. Robilem zadanie 8
i dowodzilem ze czworokat jest rowny ABR a nie APR... jak nietrudno zgadnac nie chcialo mi
wyjsc. W kazdym badz razie rozwiazanie:
Zadanie 8
 No więc Trójkąty te mają wspólny bok |DM|. Wprowadzę pewne kąty:
∡DSC = β , ∡DSA = 180o − β
Policzę te pola następująco:
PΔAMD = PΔASD − PΔASM
PΔDMC = PΔDSC − PΔCSM
No więc Trójkąty te mają wspólny bok |DM|. Wprowadzę pewne kąty:
∡DSC = β , ∡DSA = 180o − β
Policzę te pola następująco:
PΔAMD = PΔASD − PΔASM
PΔDMC = PΔDSC − PΔCSM


 Zadanie 8
T: PCPRQ = PARP
* PARP = 2PCRR
(mają tę samą wysokość opuszczoną na podstawę oraz podstawy są w stosunkach 2 : 1)
** PBRQ = 2PCQR
(mają tę samą wysokość opuszczoną na podstawę oraz podstawy są w stosunkach 2 : 1)
Zadanie 8
T: PCPRQ = PARP
* PARP = 2PCRR
(mają tę samą wysokość opuszczoną na podstawę oraz podstawy są w stosunkach 2 : 1)
** PBRQ = 2PCQR
(mają tę samą wysokość opuszczoną na podstawę oraz podstawy są w stosunkach 2 : 1)

 psik u Ciebie? A co jeśli punkt będzie leżał poza punktem S? Tak jak w tym wypadku
psik u Ciebie? A co jeśli punkt będzie leżał poza punktem S? Tak jak w tym wypadku  ?
?
 zadanie 10
△ASG jest przystający △AES bkb
△CGS jest przystający △CSF bkb
△FSB jest przystający △SEB bkb
więc
c=a−r+b−r
−2r=c−a−b
2r=a+b−c
zadanie 10
△ASG jest przystający △AES bkb
△CGS jest przystający △CSF bkb
△FSB jest przystający △SEB bkb
więc
c=a−r+b−r
−2r=c−a−b
2r=a+b−c
 , bo dziecinnie proste
, bo dziecinnie proste 
 , czuje ze zaraz wyjdzie
, czuje ze zaraz wyjdzie

 Ale to dopiero wieczorem, tj za 1−2h. Najwazniejsze mecze
ligi hiszpanskiej sie zaczely wiec zadania musza poczekac.
Ale to dopiero wieczorem, tj za 1−2h. Najwazniejsze mecze
ligi hiszpanskiej sie zaczely wiec zadania musza poczekac.
 Dobra idę na film "Wieczny student"
Dobra idę na film "Wieczny student" 

 Zaraz sprobujemy znalezc blad.
Zaraz sprobujemy znalezc blad. 
 To teraz pewnie bez wiekszych problemow pojdzie.
Sry ze pisze post pod postem xD
To teraz pewnie bez wiekszych problemow pojdzie.
Sry ze pisze post pod postem xD

 W kazdym badz razie jak ci sie zechce to mozesz napisac rozwiazanie xD
W kazdym badz razie jak ci sie zechce to mozesz napisac rozwiazanie xD
 teraz powtarzam polski <
teraz powtarzam polski < >
>





 Można inaczej: zauważyć, że trójkąty są podobne wyznaczamy h w zależności:
h = h1 + h2 i porównujemy pola
Można inaczej: zauważyć, że trójkąty są podobne wyznaczamy h w zależności:
h = h1 + h2 i porównujemy pola 
 ? Męczę się z tym już kupę czasu i nadal nic...
? Męczę się z tym już kupę czasu i nadal nic...

 jasne kwiaty
jasne kwiaty 

 Zad.11/ ( treść zadania wyżej podana przez rumpek
Zad.11/ ( treść zadania wyżej podana przez rumpek

 "gdzie są chłopcy z tamtych lat" ? (pewnie ...
"gdzie są chłopcy z tamtych lat" ? (pewnie ... 


 Eta
Eta  Wakacje na mnie źle działają
Wakacje na mnie źle działają  zapominam wiele ciekawych rzeczy i proste zadania stają się
trudne
zapominam wiele ciekawych rzeczy i proste zadania stają się
trudne 


