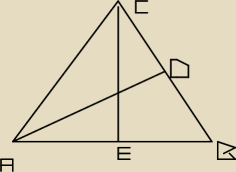
 Dany jest trójkąt równoramienny ABC, |AB| = |BC|, o obwodzie 200 cm. W trójkącie tym
poprowadzono środkowe AD i CE. Obwód trójkąta ACE jest o 20cm większy od obwodu trójkąta
ABD. Oblicz długości boków trójkąta ABC.
Dany jest trójkąt równoramienny ABC, |AB| = |BC|, o obwodzie 200 cm. W trójkącie tym
poprowadzono środkowe AD i CE. Obwód trójkąta ACE jest o 20cm większy od obwodu trójkąta
ABD. Oblicz długości boków trójkąta ABC.



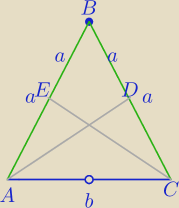 1)
4a+b=200
lΔACE=b+a+|EC|
lΔBD=3a+|AD| i |AD|=|EC|=s
2)
b+a+s−20=3a+s
b=20+2a
3)
4a+20+2a=200
6a=180
a=30
|AB|=|BC|=60
|AC|=80
======
1)
4a+b=200
lΔACE=b+a+|EC|
lΔBD=3a+|AD| i |AD|=|EC|=s
2)
b+a+s−20=3a+s
b=20+2a
3)
4a+20+2a=200
6a=180
a=30
|AB|=|BC|=60
|AC|=80
======