geometria
heeeeeeelp:
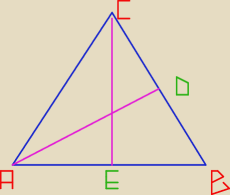
Dany jest trójkąt równoramienny ABC, |AB| = |BC|, o obwodzie 200 cm. W trójkącie tym
poprowadzono środkowe AD i CE. Obwód trójkąta ACE jest o 20cm większy od obwodu trójkąta
ABD. Oblicz długości boków trójkąta ABC.
21 kwi 18:10
tim: Masz odp?
21 kwi 18:17
heeeeeeelp: tak |AC|=80cm, |AB| = |BC| = 60cm
21 kwi 18:18
tim: Ok. Tyle mi wyszło

Już piszę.
21 kwi 18:21
tim:
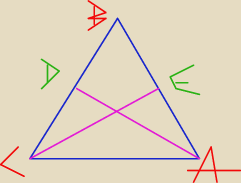
Pozwolisz, że na rysunku obrócę ten trójkąt

Wiemy, że |BC| = |BA|, wnioskuję z tego, że środkowe są równej długości (|AD| = |CE|)
Układamy układ równań:
dla x = |BC| = |BA|, y = |AC|, z = |CE| = |AD|
2x + y = 200
y + 0,5x + z = x + 0,5x + z + 20 [boki trójkątów]
Rozwiązujemy:
x = 60
|BC| = |AB| = 60
|AC| = 200 − 120 = 80
Zaraz będzie dowód równości dwusiecznych

21 kwi 18:24
tim: Środkowych*

21 kwi 18:24
tim: Długość środkowej d opadającej na bok c wynosi:
Gdzie u nas dla środkowej opadającej na |BC| =
Gdzie u nas dla środkowej opadającej na |AB| =
Są równe

21 kwi 18:26
heeeeeeelp: dzięki Tim boski jesteś

21 kwi 18:31
21 kwi 18:36
heeeeeeelp: pomożesz jeszcze z jednym ? prosze
21 kwi 18:38
tim: Które? Jak będę umiał to tak [w końcu mam tylko 14 lat]
21 kwi 18:39
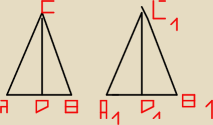
heeeeeeelp: w Trójkątach ABC i A1B1C1 poprowadzono dwusieczne CD i C1D1. Uzasadni, że trójkąt
ABC jest przystający do trójkąta A1B1C1, wiedząc, że |CD| = |C1D1|, |DA| = |D1A1|
oraz |kątCDA| = |kąt C1D1A1|
21 kwi 18:41
heeeeeeelp: tak tak a ja 8

21 kwi 18:42
tim: O to nie..

ja... Załóż nowy temat.. Bogdan powinien pomóc

21 kwi 18:42
tim: Naprawdę −.−'... Bogdan wczoraj zaświadczał

21 kwi 18:43
heeeeeeelp:
21 kwi 18:44
heeeeeeelp: ale na co mam ten temat założyć? na zadanie?
21 kwi 18:45
tim: Tak

.. Tzn. dodaj nowe zadanie

21 kwi 18:45
heeeeeeelp: ok dzięki

21 kwi 18:46
 Dany jest trójkąt równoramienny ABC, |AB| = |BC|, o obwodzie 200 cm. W trójkącie tym
poprowadzono środkowe AD i CE. Obwód trójkąta ACE jest o 20cm większy od obwodu trójkąta
ABD. Oblicz długości boków trójkąta ABC.
Dany jest trójkąt równoramienny ABC, |AB| = |BC|, o obwodzie 200 cm. W trójkącie tym
poprowadzono środkowe AD i CE. Obwód trójkąta ACE jest o 20cm większy od obwodu trójkąta
ABD. Oblicz długości boków trójkąta ABC.
 Już piszę.
Już piszę.
 Pozwolisz, że na rysunku obrócę ten trójkąt
Pozwolisz, że na rysunku obrócę ten trójkąt  Wiemy, że |BC| = |BA|, wnioskuję z tego, że środkowe są równej długości (|AD| = |CE|)
Układamy układ równań:
dla x = |BC| = |BA|, y = |AC|, z = |CE| = |AD|
2x + y = 200
y + 0,5x + z = x + 0,5x + z + 20 [boki trójkątów]
Rozwiązujemy:
x = 60
|BC| = |AB| = 60
|AC| = 200 − 120 = 80
Zaraz będzie dowód równości dwusiecznych
Wiemy, że |BC| = |BA|, wnioskuję z tego, że środkowe są równej długości (|AD| = |CE|)
Układamy układ równań:
dla x = |BC| = |BA|, y = |AC|, z = |CE| = |AD|
2x + y = 200
y + 0,5x + z = x + 0,5x + z + 20 [boki trójkątów]
Rozwiązujemy:
x = 60
|BC| = |AB| = 60
|AC| = 200 − 120 = 80
Zaraz będzie dowód równości dwusiecznych 



 Wiem
Wiem


 ja... Załóż nowy temat.. Bogdan powinien pomóc
ja... Załóż nowy temat.. Bogdan powinien pomóc 


 .. Tzn. dodaj nowe zadanie
.. Tzn. dodaj nowe zadanie 
