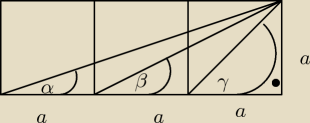
udowodnij, że ralka: Udowodnij, że α + β = γ proszę o pomoc

Ajtek:

	a
tgγ=		=1
	a

	a		1
tgβ=		=
	2a		2

	a		1
tgα=		=
	3a		3

Jeżeli α+β=γ to tgγ=tg(α+β)

	1   1   + 3   2		5   6
tg(α+β)=		=		=1
	1   1   1− *   2   3		5   6

zatem α+β=γ c.n.u.

Eta:

Ajtek: Eta witaj. Jabłuszko od Ciebie to więcej jak Nobel!

Eta: Dzięki ........... i czuj się,że dostałeś jabłkowego Nobla

Ajtek: Tak też się czuję .

Eta:

Ralka: Za zadne skarby nie mogezrozumiec rownania   tg(α+β)=... Moge prosic o wytlumaczenie?

Ajtek: Tutaj masz ten wzorek: 1543

Ralka: Ok, dzieki a nie masz moze pomyslu jak to wyprowadzic?

Ajtek: Dowód chcesz?

Ralka: Chodzi mi o to skad sie wzial ten wzor − w tablicach go nie ma, da sie go jakos na szybko wuprowadzic czyraczej trzeba zapamietac? Przepraszam za bledy ale nie pisze na komputerze..

Ajtek: To jest wzorek z rozszerzenia. Wyprowadzić go trudno w sumie nie jest, tylko najpierw trzeba zrobić dowodzik na sin(x+y) i cos(x+y). Ewentualnie przyjąć, że w.w. dowody znamy, to zrobienie będzie chwilą.

Ralka: Dobra, pobawie sie z tym dzieki za pomoc

Ajtek: Będę po 21−szej, to zerknę i ewentualnie pomogę.

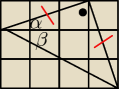
Vax: Da się bez funkcji trygonometrycznych..