planimetria Kinaa: Dany jest trapez równoramienny o kącie prostym między przekątnymi i stosunku długości podstaw 1:5. Oblicz pole i obwód tego trapezu,jeśli wiadomo że długość dłuższej podstawy jest równa 20

arti: obwód 40 a pole 96 cm²

arti: wiesz z kad?

Amber: może ktoś mi dać jakąś podpowiedź do tego zadania?

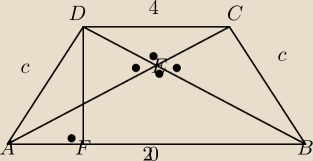
Amber: wiem, że ten obrazek nie jest za piękny, piękniej nie umiem jakaś podpowiedź? trójkąt AED i DFA są podobne i co dalej?

Amber: podbijam?

Amber: wiem, że jestem nachalna, ale mam dosyć mało czasu.

Janek191:

	1
PΔCDE = 0,5 *		*42 = 4
	2

	1
PΔABE = 0,5*		202 = 100
	2

oraz I CE I² = 2*4 ⇒ I CE I = 2√2 I BE I² = 2*100 ⇒ I BE I = 10 √2 więc P_ΔBCE = P_ΔADE =0,5* I CE I* I BE I = 0,5*2√2*10√2 = 20 więc pole trapezu ABCD jest równe P = 4 + 100 + 2*20 = 144 ===================== c² = I CE I² + I BE I² = 8 + 200 = 208 = 16*13 c = 4 √13 ========== Obwód trapezu L = 20 + 4 + 2* 4√13 = 24 + 8√13 ==============================

Janek191:

	1
PΔCDE = 0,5 *		*42 = 4
	2

	1
PΔABE = 0,5*		202 = 100
	2

oraz I CE I² = 2*4 ⇒ I CE I = 2√2 I BE I² = 2*100 ⇒ I BE I = 10 √2 więc P_ΔBCE = P_ΔADE =0,5* I CE I* I BE I = 0,5*2√2*10√2 = 20 więc pole trapezu ABCD jest równe P = 4 + 100 + 2*20 = 144 ===================== c² = I CE I² + I BE I² = 8 + 200 = 208 = 16*13 c = 4 √13 ========== Obwód trapezu L = 20 + 4 + 2* 4√13 = 24 + 8√13 ==============================

Amber: wszystko kapuję, ale z jakiego wzoru to pole CDE i ABE?

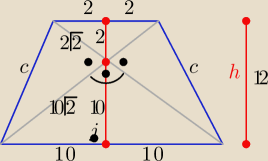
Eta: Nie ma sensu aż tak się rozpisywać

	20+4
h= 12 , P=		*h= 12*12= 1442]
	2

c= √(10√2)²+(2√2)²= √208= 4√13 Ob= 24+8√13 [j]

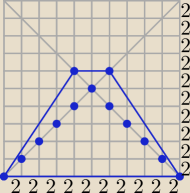
Bogdan: Może taki rysunek ułatwi rozwiązanie

RS: Bogdan mógłbyś zerknąć ? https://matematykaszkolna.pl/forum/229819.html chodzi o to zadnie ze środkową.