;
RS:
Napisz równanie okręgu przechodzącego przez punkt P(9,9) i stycznego do osi Ox w punkcie
Q(6 ,0)
Myślałem że środek tego odcinka to będzie środek tego okręgu a promień to połowa długości ale
jednak nie

3 sty 17:47
RS:
Środek będzie miał pierwszą współrzędną (6,b) ?
3 sty 17:49
RS:
Już wiem o co chodzi

3 sty 17:54
PanMieczysław: Sam sobie pytania zadajesz i sam odpowiadasz?
Po co? Po to.
Jaki? Taki.
Ile? Tyle.
Kabaret Neonówka, The Sejm, Polecam.
3 sty 17:56
RS:
Punkty A = (− 2,0) i B = (8,0) są wierzchołkami trójkąta prostokątnego ABC o
przeciwprostokątnej AB i polu równym 15. Oblicz współrzędne punktu C
Mam tylko wyznaczoną długość odcinka a dalej potrzebuje wskazówki ?
3 sty 17:56
Mila:
Tak.
R=b
3 sty 17:57
RS:
@Pan Mieczysław chyba kłania się szkoła podstawowa i ortografia ''Po tak'' ? Polecam słownik
poprawnej polszczyzny.

3 sty 17:59
RS:
A odnośnie zadanie 17:56 ?
3 sty 18:00
RS:
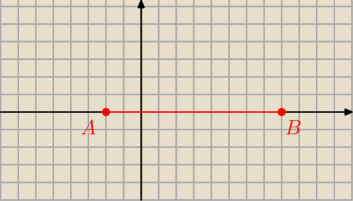
Mogą wyjść dwie możliwości dla punktu C ?
3 sty 18:05
Mila:
Rysunek
1) |AB|=...
2) oblicz wysokość Δ ze wzoru na pole.
| | −2+8 | | 1 | |
3) napisz równanie okręgu o środku( |
| ,0) i promieniu |
| |AB| |
| | 2 | | 2 | |
.....
3 sty 18:08
Mila: 4 rozwiązania.
3 sty 18:09
RS:
Skoro AB jest przeciwprostokątną czyli jest średnicą tego okręgu ? Można spróbować z trójkąta
wpisanego w okrąg ? Tylko nie wiem czy to coś da. ?
3 sty 18:11
PanMieczysław: @RS Absolutnie. Jestem studentem, a czasem miewam dziwne pomysły. A co do ortografii...nie
rozumiem twojego stwierdzenia.
3 sty 18:15
Mila:
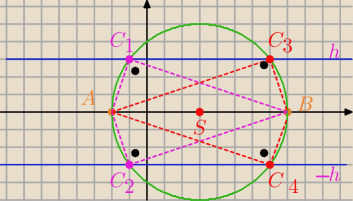
S=(3,0) R=5
h=3
Masz 4 Δ prostokątne.
Jeśli masz pytania, to pisz.
3 sty 18:19
RS:
Mila ale jeśli AB jest średnicą,to czy ta średnica nie powinna przechodzić przez środek okręgu
?
3 sty 18:21
Mila:
No przecież AB jest średnicą. Popatrz uważnie na rysunek.
Kąty :
AC1B,
AC2B,
AC3B,
AC4B, to kąty wpisane w okrąg oparte na średnicy i są proste.
3 sty 18:30
RS:
Racja, przepraszam źle spojrzałem.
3 sty 18:31
RS:
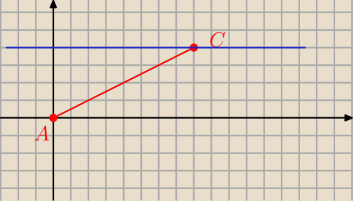
Punkty A = (0,0) i C = (8,4) są wierzchołkami rombu ABCD , którego jeden z boków zawiera się
w prostej y = 4 . Wyznacz współrzędne pozostałych wierzchołków rombu
Prosta równoległa do prostej AC odpada bo nie mam żadnego punktu ?
Punkt symetrii ?
3 sty 18:46
Eta:
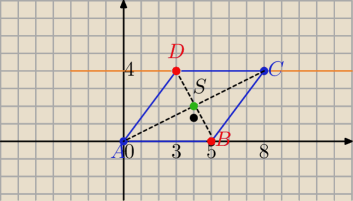
3 sty 19:09
RS:
A jakąś wskazówkę można prosić ? Co z tym punktem symetrii ?
3 sty 19:11
Piotr 10: Wyznacz wpierw środek, potem wiesz, że D(x;4), czyli policzysz już druga wspołrzędną punktu B
3 sty 19:13
Piotr 10: Albo od razu zauważysz, że B(xb;0)
Potem wyznacz równanie prostej AC, następnie równanie prostej DB prostopadłej do prostej AC
3 sty 19:16
Mila:
1) Piszesz równanie prostej AC ( patrz rysunek Ety
2) Piszesz równanie symetralnej odcinka AC.
3) punkty przecięcia symetralnej z osią Ox i prostą y=4 , to będą Punkty B i D
3 sty 19:38
Eta:
D(x
D,4) , B(x
B,0) , S(4,2)
z tw. Pitagorasa |AS|
2+|BS|
2= |AB|
2 ⇒ x
B=...
x
D= 2x
S−x
B=....
i to wszystko

3 sty 19:43
RS:
Dana jest prosta k o równaniu x+y−12=0 oraz punkt M (− 5;9) wyznacz na prostej k takie
punkty P i R aby |MP|=|MR|=8
x+y−12=0
y=−x+12
MP=
√(−5−x)2+(9+x−12)2=8
MP=
√x2+10x+25+x2−6x+8=8 /
2
x
2+10x+25+x
2−6x+9=64
2x
2+4x−30=0 /2
x
2+2x−15=0
Δ=64
√Δ=8
y
1=5+12=17
y
2=9
Co dalej ? Czy to są współrzędne obu punktów czy tylko MP ?
3 sty 20:02
RS:
i długość wychodzi 8
√2 więc źle bo ma być 8

3 sty 20:07
RS: ?
3 sty 20:34
matyk: To będą oba potrzebne rozwiązania. Sprawdź w takim razie rachunki

3 sty 20:51
RS:
Rachunki są ok ale dalej lipa.
3 sty 20:52
Mila:
Trzeba zrobić szkic sytuacji w układzie wsp.
M=(−5,9)
R=(3,9)
|MR|=8
P=(−5,17)
|MP|=√(−5+5)2+(17−9)2=√82=8
3 sty 21:05
RS:
Dziękuję. Czyli ja wyznaczałem od razu współrzędne obu punktów ?
3 sty 21:17
Mila:
Zgadza się.
3 sty 21:21
RS:
Mogę jeszcze liczyć na pomoc z Twojej strony ?
3 sty 21:25
Mila:
Jeszcze będę kilka minut. Pisz.
3 sty 21:26
RS:
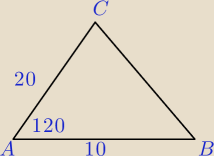
Mam takie zadnie w arkuszu ale nie wiem czy mogę tak to rozwiązać aby uzyskać max punktów
W trójkącie ABC mamy dane |AB|=10cm |AC|=20cm i |∡BAC=120
0| Wyznacz długość środkowej
cos120
0=−cos60
0=−0.5
|BC|
2=20
2+10
2−[2*10*20*(−0,5)]
|BC|
2=400+100−(−200)
|BC|
2=700
|BC|=10
√7 lub |BC|=−10
√7∉R
+ bok nie może być ujemny
długość środkowej wyraża się wzorem
d=0,5
√2a2+2b2−c2
c−długość boku na który pada śrdokowa
a−bok trójkąta
b−bok trójkąta
d=0,5
√2*202+2*102−(10√7)2
d=0,5
√2*400+2*100−700
d=0,5
√800+200−700
d=0,5
√300
d=0,5*10
√3
d=5
√3 cm
Długość środkowej AD wynosi 5
√3cm
Czy dostałbym max punktów ?
3 sty 21:33
RS:
wyznacz długość środowej AD zapomniałem dopisać w poleceniu.
3 sty 21:37
Eta:
ok

4 sty 00:52
RS:
Czyli 6% już mam

Dziękuję

4 sty 00:56
Bogdan:
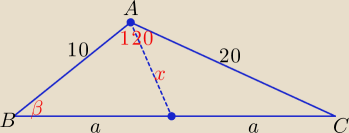
| | 1 | |
cos120o = − |
| i a>0 i x>0 |
| | 2 | |
| | 1 | |
Z tw. kosinusów:4a2 = 100 + 400 + 2*10*20* |
| = 700 ⇒ 2a = 10√7 ⇒ a = 5√7 |
| | 2 | |
| | 400 | | 2 | |
oraz 400 = 100 + 700 − 2*10*5√7*cosβ ⇒ cosβ = |
| = |
| |
| | 200√7 | | √7 | |
| | 2 | |
x2 = 100 + 175 − 2*10*5√7* |
| = 75 ⇒ x = 5√3 |
| | √7 | |
Nie pisz oznaczeń w słupku (to paskudna maniera), czyli
d =
d =
d =
A teraz sam oceń, czy dostałbyś maksimum punktów.
4 sty 01:17
Bogdan:
Ponadto nie mówimy "bok nie może być ujemny", ale "długość boku nie może być ujemna"
4 sty 01:19
Eta:

4 sty 01:28



 Mogą wyjść dwie możliwości dla punktu C ?
Mogą wyjść dwie możliwości dla punktu C ?
 S=(3,0) R=5
S=(3,0) R=5
 Punkty A = (0,0) i C = (8,4) są wierzchołkami rombu ABCD , którego jeden z boków zawiera się
w prostej y = 4 . Wyznacz współrzędne pozostałych wierzchołków rombu
Prosta równoległa do prostej AC odpada bo nie mam żadnego punktu ?
Punkt symetrii ?
Punkty A = (0,0) i C = (8,4) są wierzchołkami rombu ABCD , którego jeden z boków zawiera się
w prostej y = 4 . Wyznacz współrzędne pozostałych wierzchołków rombu
Prosta równoległa do prostej AC odpada bo nie mam żadnego punktu ?
Punkt symetrii ?




 Mam takie zadnie w arkuszu ale nie wiem czy mogę tak to rozwiązać aby uzyskać max punktów
W trójkącie ABC mamy dane |AB|=10cm |AC|=20cm i |∡BAC=1200| Wyznacz długość środkowej
cos1200=−cos600=−0.5
|BC|2=202+102−[2*10*20*(−0,5)]
|BC|2=400+100−(−200)
|BC|2=700
|BC|=10√7 lub |BC|=−10√7∉R+ bok nie może być ujemny
długość środkowej wyraża się wzorem
d=0,5√2a2+2b2−c2
c−długość boku na który pada śrdokowa
a−bok trójkąta
b−bok trójkąta
d=0,5√2*202+2*102−(10√7)2
d=0,5√2*400+2*100−700
d=0,5√800+200−700
d=0,5√300
d=0,5*10√3
d=5√3 cm
Długość środkowej AD wynosi 5√3cm
Czy dostałbym max punktów ?
Mam takie zadnie w arkuszu ale nie wiem czy mogę tak to rozwiązać aby uzyskać max punktów
W trójkącie ABC mamy dane |AB|=10cm |AC|=20cm i |∡BAC=1200| Wyznacz długość środkowej
cos1200=−cos600=−0.5
|BC|2=202+102−[2*10*20*(−0,5)]
|BC|2=400+100−(−200)
|BC|2=700
|BC|=10√7 lub |BC|=−10√7∉R+ bok nie może być ujemny
długość środkowej wyraża się wzorem
d=0,5√2a2+2b2−c2
c−długość boku na który pada śrdokowa
a−bok trójkąta
b−bok trójkąta
d=0,5√2*202+2*102−(10√7)2
d=0,5√2*400+2*100−700
d=0,5√800+200−700
d=0,5√300
d=0,5*10√3
d=5√3 cm
Długość środkowej AD wynosi 5√3cm
Czy dostałbym max punktów ?

 Dziękuję
Dziękuję 

