geometria Klaudia: Dany jest trójkąt o wierzchołkach A(−1,1), B(3,−1), C(1,3). Podaj punkt przecięcia się jego boków z osiami układu współrzędnych.

Życzliwa: Musisz najpierw wyznaczyć równania prostych zawierających każdy kolejny bok trójkąta. Korzystając ze wzoru na równanie prostej przechodzącej przez dwa punkty: czyli np: pierwszy bok AB y−1=[(1+1)/(−1−3)]*(x+1) z tego otrzymujemy: y=(−1/2)x+1/2 Teraz rozwiązujesz układ równań {y=(−1/2)x+1/2 {y=0 z tego otrzymasz punkt przecięcia boku AB z osią 0X, a z układu: {y=(−1/2)x+1/2 {x=0 punkt przecięcia boku AB z osią 0Y. Pierwszy punkt to (1,0), a drugi (0,1/2). Analogicznie robisz pozostałe boki.

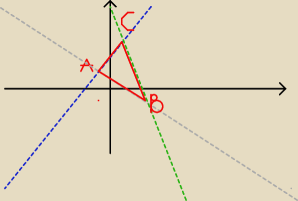
xpt: musisz wyznaczyć równania prostych na których leżą boki tego trójkąta |AC|, |AB|, |BC| Pożniej wyznaczasz ich przecięcia z oziami x i y.[ Potrzebne zrozy masz tutaj 1223

xpt: Życzliwa meni ubiegła, ale ja zrobiłem ładny rysunek :P

Bogdan: Trzeba utworzyć równania prostych zawierających wierzchołki trójkąta. Dla prostej z punktami A, B: współczynnik kierunkowy a₁ = ^{−1 − 1}_{3 − (−1)} = ⁻²₄ = ⁻¹₂ Korzystamy z wzoru: y − y₁ = a(x − x₁), gdzie (x₁, y₁) to współrzędne punktu A lub B, wybieram punkt A(−1, 1): y − 1 = ⁻¹₂(x + 1) y = −¹₂x − {1}{2} + 1 y = −¹₂x + ¹₂ Teraz wyznaczamy punkty przecięcia tej prostej z osiami: z osią x: y = 0 => −¹₂x + ¹₂ = 0 => x = 1 z osią y: x = 0 => y = −¹₂ W ten sam sposób postępujemy z prostymi zawierającymi punkty A, C oraz B, C.

Bogdan: Poprawka (wkradł się chochlik): z osią y: x = 0 => y = ¹₂

Klaudia: dzieki bardzo !