Z góry
ogromnie dziekuje za wszelka pomoc.
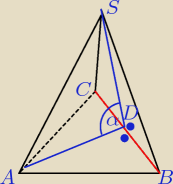podstawa w czworościanie foremnym jest taką samą ścianą jak każda inna
| a√3 | ||
AD = SD = hb = | ||
| 2 |
| ||||||||
a czy nie wystarczy po prostu podstawic i wyliczyc ze cosα= | ? | |||||||
| a |
ehh.. potrzebuje
wysokosc ostroslupa, tak?
| 1 | 1 | a√3 | a√3 | |||||
PD = | hb = | * | = | |||||
| 3 | 3 | 2 | 6 |
| PD | a√3 | 2 | 1 | |||||
cosα = | = | * | = | |||||
| DS | 6 | a√3 | 3 |
* Na czerwono zaznaczyłem kąt dwuścienny, najłatwiej obliczyć go korzystając z tw. cosinusów,
które wygląda tak: a2 = b2 + c2 − 2bccosα. Skoro mamy podane, że jest to czworościan
foremny to odcinki |BD| = |AD| = wysokości ścian bocznych. Tak jak ty chcesz obliczyć,
niestety w tym przypadku nie ma tam nigdzie kąta prostego, aby można łatwo obliczyć. Możesz
równie dobrze kombinować tak, że: puścić wysokość tego kąta na odcinek |AB| i potem właśnie
| π | ||
liczyć z funkcji trygonometrycznych  Wyznaczysz wtedy odpowiednio cos | , i potem | |
| 2 |
Czyli tw. cosinusów i styka.
| a√3 | a√3 | a√3 | ||||
* a2 = ( | )2 + ( | )2 − 2( | )2cosα | |||
| 2 | 2 | 2 |
| 3a2 | 3a2 | 3a2 | ||||
a2 = | + | − 2 * | cosα | |||
| 4 | 4 | 4 |
| 6a2 | 3a2 | |||
a2 = | − | cosα | ||
| 4 | 2 |
| 3a2 | 3a2 | |||
a2 = | − | cosα | ||
| 2 | 2 |
| 3a2 | ||
a2 = | (1 − cosα) / * 2 | |
| 2 |
| 2a2 | |
= 1 − cosα | |
| 3a2 |
| 2 | |
− 1 = − cosα | |
| 3 |
| 2 | 3 | ||
− | = −cosα | ||
| 3 | 3 |
| −1 | |
= −cosα | |
| 3 |
| 1 | ||
cosα = | ||
| 3 |
* Dodam, że jak masz podane kąt dwuścienny lub "kąt między dwoma sąsiednimi ścianami" − to
jest to samo, to właśnie boki tego kąta padają prostopadle do boków ścian bocznych ostrosłupa
doceniam to bardzo i dziękuję ogromnie za pomoc!
jeśli pozwolisz, mam kilka pytań.
1) bo cholercia zawsze mam problem z zaznaczeniem tego kata dwusciennego, czyli jesli dobrze
rozumiem, tworzy sie on we wspolnym miejscu spodkow wysokosci sasiednich scian bocznych? (mam
nadzieje,ze rozumiesz co mam na mysli 
)
2) moglbys mi troszke rozjasnic to tw. cosinusow? kiedy go sie stosuje, i czym jest zawsze to a
b c i bc, ktore sa we wzorze? nie chcialabym na głupa przepisywac, tylko chce rozumiec czym
jest a, b itd i tez umiec wykorzystac w innych sytuacjach, jesli zauwaze,ze warto skorzystac
lub nic innego mi nie przyjdzie do głowy
z góry dziękuję za wyjasnienie
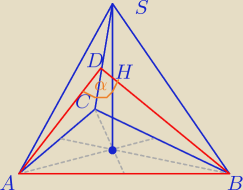
Tak to jeszcze jedno rozwiązanie twoje Basiu to można jeszcze tak jak napisałem robić
| α | ||
wyznaczyć wysokość z tego kąta i potem będzie cos | , i łatwo doprowadzić do formy cosα | |
| 2 |
czy Basiu moglabys pokazac ten sposob bez korzystania
z tw. cos?
jeśli możesz mi tylko wyjasnic skad pewnosc (byc moze jest taka wlasnosc,ktorej najwidoczniej
nie znam) PD jest 1/3 wysokosci sciany bocznej?
dziękuję Wam ogromnie czy moge prosic Was o pomoc jeszcze z jednym
KOSZMARNYM zadankiem? naprawdę choć mam dobre chęci to nic z tego nie wychodzi...
1. Pole przekroju ostrosłupa prawidlowego trojkatnego plaszczyzną przechodzacą przez wysokosc
podstawy i krawedz boczną, wychodzacymi z tego samego wierzcholka, wynosi 45 dm2, a wysokosc
ostroslupa jest rowna 5 dm. Oblicz:
a) sinus kata nachylenia krawedzi bocznej do plaszczyzny podstawy
b) tanges kata nachylenia sciany bocznej do plaszczyzny podstawy
c) objetosc tego ostroslupa.
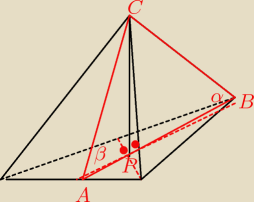ten przekrój to ABC
H ostrosłupa jest też wysokością tr.ABC
AB wysokość podstawy (tr.równobocznego)
a − krawędź podstawy
| a√3 | ||
AB = | ||
| 2 |
| 2a√3 | a√3 | |||
BP = 23AB = | = | |||
| 6 | 3 |
| a√3 | ||
AP = 13AB = | ||
| 6 |
| 1 | 1 | a√3 | 5a√3 | |||||
P = | *AB*PC = | * | *5 = | |||||
| 2 | 2 | 2 | 4 |
| 5a√3 | |
= 45 | |
| 4 |
jesteś wspaniała Basiu