Zadanka
Godzio: Ciekawe zadania
Jest ktoś zainteresowany ciekawszymi zadankami (np.
Basiek 
). Wiem, że jest nastrój
świąteczny dlatego pytam
5 kwi 20:53
Przewiduje pokój: Pytasz a nie zmuszasz
5 kwi 20:55
Godzio:
Nigdy nie zmuszam, każdy robi co chce
5 kwi 20:56
Przewiduje pokój: Możesz dać
5 kwi 20:57
Baś: Godzio 
jak słodko
5 kwi 20:58
Godzio:
| | 8 | |
W trójkącie ABC dane są promień okręgu opisanego R, kąt ∡A = α oraz |AB| = |
| R. |
| | 5 | |
Obliczyć pole tego trójkąta. (Od razu podpowiem, że nie ma jednego wyniku
)
5 kwi 20:59
Baś: Planimetria...
to by było na tyle.
5 kwi 21:01
Godzio:
W takim razie, to zadanie zrobi kolega
Pp 
Baś z czego chcesz zadanie, dostosuje się
5 kwi 21:01
Jack:
pamiętam to zadanie
Od
Vaxa, zdaje się
5 kwi 21:02
Godzio:
A nie wiem, ja go wziąłem z mojego zbiorku
5 kwi 21:03
Jack:
jakiego?
5 kwi 21:06
Baś: Godzio, ja chociaż spróbuję, dobrze?
5 kwi 21:07
5 kwi 21:07
Godzio:
Dobrze
Nie chce, żebyście się zanudzili matematyką wyznaczając ciągle dziedzinę funkcji, mi
Eta podrzucała co chwilę jakieś fajniejsze zadanka
5 kwi 21:08
Jack:
nawet go mam
Zadaję z niego zadanka ludziom − widać ominąłem to zadanie
5 kwi 21:08
Przewiduje pokój: robię ale chyba jakoś bardzo okrężną drogą bo straszne wyniki wychodzą
5 kwi 21:09
Baś: Ja chyba odpadłam
pojawiła mi się zmienna
y i nie chce się cholera odczepić
5 kwi 21:12
Godzio:
Rób
Wyniki nie muszą być ładne (
Jack 22,4)
5 kwi 21:12
Przewiduje pokój: chociaż mam pomysł
5 kwi 21:13
Godzio:
Sprawdziłem w moich rozwiązaniach i zobaczyłem, że tego zadania nie mam zrobionego co oznacza,
że sprawiło mi problem, a co za tym idzie, też się za nie zabieram
5 kwi 21:18
Baś: Jest paskudne, naprawdę. Można w nim bez problemu wylicz maaasę rzeczy. Pomijając te, które są
niezbędne do policzenia pola.
Godzio − zarzuć czymkolwiek, byle nie stereometrią i planimetrią
5 kwi 21:20
Przewiduje pokój: Godziu jak ci wyśle rozwiązanie na maila to sprawdzisz?
5 kwi 21:21
Godzio:
Dla jakich wartości parametru p nierówność:
| 2px2 + 2px + 1 | |
| ≥ 2 |
| x2 + x + 2 − p2 | |
jest spełniona dla każdej liczby rzeczywistej x ?
5 kwi 21:22
Godzio:
Sprawdzę
5 kwi 21:22
Przewiduje pokój: To jeszcze przepiszę
5 kwi 21:23
Baś: Super, dzięki
To robię !
5 kwi 21:24
Przewiduje pokój: Kamera mi niestety ucieła troszkę ale jestem pewien że domyślisz się co tam powinno być
Napisz co o tym sądzisz
5 kwi 21:32
Baś: Ech, mam dziwne "przeczucie", że wszystko źle, ale co tam
Za ładnie wyszło ...
5 kwi 21:37
Eta:
zad. z trójkątem P= 8R
2sinα(3sinα+4cosα)
5 kwi 21:41
Przewiduje pokój: Eta a to nie jest podzielone przez 5 przypadkiem ?
5 kwi 21:42
Ole:
Zad z trójkatem
| | 32 | | R2tgα | |
P= |
| * |
| |
| | 25 | | 1 + 3/4tgα | |
5 kwi 21:42
Godzio:
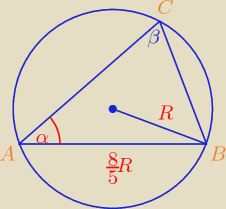
P = ?
Z twierdzenia sinusów mamy:
| |AB| | | | | 4 | |
| = 2R ⇒ |
| = 2R ⇒ sinβ = |
| |
| sinβ | | sinβ | | 5 | |
| |CB| | |
| = 2R ⇒ |CB| = 2Rsinα |
| sinα | |
| | 1 | | 1 | | 8 | |
P = |
| sin(180 − (α + β) ) * |AB| * |CB| = |
| sin(α + β) * |
| R * 2Rsinα = |
| | 2 | | 2 | | 5 | |
| | 8 | |
= |
| R2sinα * (sinαcosβ + cosαsinβ) |
| | 5 | |
| | 3 | |
1o β jest kątem ostrym, wówczas cosβ = |
| |
| | 5 | |
| | 8 | | 3 | | 4 | |
P1 = |
| R2sinα * (sinα * |
| + cosα * |
| ) = |
| | 5 | | 5 | | 5 | |
| | 8 | |
= |
| R2sinα(3sinα + 4cosα) |
| | 25 | |
Teraz przyjrzyjmy się wynikowi pole musi być dodatnie, zatem dla α ostrego jest ok, dla α
rozwartego musimy zapewnić, że pole jest dodatnie, zatem:
3sinα + 4cosα > 0
3sinα > 4
√1 − sin2α( bo cosinus jest ujemny), po podniesieniu do kwadratu:
| | 16 | | 4 | |
9sin2α > 16 − 16sin2α ⇒ 25sin2α > 16 ⇒ sin2α > |
| ⇒ sinα > |
| |
| | 25 | | 5 | |
| | 3 | |
2o β jest kątem rozwartym, wówczas cosβ = − |
| , rozwiązanie analogiczne z tym, że: |
| | 5 | |
| | 8 | |
P2 = |
| R2sinα(−3sinα + 4cosα) |
| | 25 | |
Podsumowując:
Jeżeli α jest kątem ostrym to mamy 2 rozwiązania:
| | 8 | |
P1 = |
| R2sinα(3sinα + 4cosα) |
| | 25 | |
| | 8 | | 4 | |
P2 = |
| R2sinα(−3sinα + 4cosα) (pod warunkiem, że sinα < |
| bo pole nie może być |
| | 25 | | 5 | |
ujemne)
| | 4 | |
Jeżeli α jest kątem rozwartym i sinα > |
| |
| | 5 | |
| | 8 | |
P3 = |
| R2sinα(3sinα + 4cosα) |
| | 25 | |
| | 4 | |
Jeżeli α jest rozwarty i sinα < |
| to mamy sprzeczność, bo wówczas pole jest ujemne. |
| | 5 | |
| | 4 | |
Wypada sprawdzić co się dzieje dla sinα = |
| , dla α ostrego jest wszystko ok, |
| | 5 | |
| | 3 | | 4 | | 3 | |
dla α rozwartego, cosα = − |
| wtedy 3 * |
| − 4 * |
| = 0, wtedy nie ma co mówić o |
| | 5 | | 5 | | 5 | |
| | 4 | |
polu, więc dla sinα = |
| przy założeniu, że α jest ostry jest też ok |
| | 5 | |
To jest pełne rozwianie zadania, może nie najkrótsze, ale poprawne
5 kwi 21:46
Eta:
Ma być dzielone przez
25
5 kwi 21:47
Godzio:
Eta pisałem, że nie ma jednego rozwiązania !
Przewiduje pokój, Ty w swoim
rozwiązaniu też nie uwzględniłeś różnych przypadków !
5 kwi 21:47
Godzio:
Baś niestety zły wynik
5 kwi 21:49
Eta:
Pozostałe przypadki zostawiłam dla maturzystów
5 kwi 21:50
Przewiduje pokój: yyy uwzględniłem dwa.
5 kwi 21:50
Godzio:
Dla β owszem, ale nie dla α
5 kwi 21:53
Przewiduje pokój: | | 5 | | √7 | |
p ∊ (−1;1) suma ( |
| ; |
| )  |
| | 4 | | 2 | |
5 kwi 21:55
Przewiduje pokój: omg faktycznie
5 kwi 21:55
Godzio: | | 5 | |
Bez (−1,1) i tam zdaje się |
| domknięte |
| | 4 | |
5 kwi 21:56
Przewiduje pokój: już widze swój błąd.
5 kwi 21:57
Eta:
5 kwi 21:58
Godzio:
To co, napiszesz rozwiązanie, żeby
Baś mogła zobaczyć i
przeanalizować ?
5 kwi 21:58
Przewiduje pokój: w sumie to mogę
5 kwi 21:58
Przewiduje pokój: no chyba że nadal próbuje
Zaczekamy aż odpisze
5 kwi 21:58
Eta:
W jakiej "sumie" ?
5 kwi 21:59
Godzio: Ok
. Co tam ostatnio miałeś na analizie/algebrze ?
5 kwi 21:59
Przewiduje pokój: algebra to kongurencje a o analizie to rozmawialiśmy chyba wczoraj
5 kwi 22:00
Godzio:
Ano granice
To poczekaj, zobaczę czy mam ciekawszy przykład prócz tych z list
5 kwi 22:01
Przewiduje pokój: Godziu spokój
Wystarczy że mnie ostatnio ochrzaniłeś za indukcję
5 kwi 22:02
Godzio:
Mam 2 propozycje, po pierwsze pytanie czy pokazywaliście, że
| | 1 | |
limn→∞(1 + |
| )n istnieje |
| | n | |
oraz drugie,
| | a1 + a2 + ... + an | |
Jeśli an → a to również |
| → a (przy n →∞) |
| | n | |
5 kwi 22:04
Przewiduje pokój: my tylko liczyliśmy. Nie było żadnego pokazywania
5 kwi 22:05
Godzio:
No to pozuj ( 1 − ciąg monotoniczny i ograniczony, 2 − jeśli an → a to an = ... ? )
5 kwi 22:06
Godzio: pokazuj*
5 kwi 22:06
Przewiduje pokój: Godziu ja ci tam łatwe zadanko
Udowodnić że jeżeli dla każdego elementu a grupy G zachodzi : a
2 = 3 to grupa G jest abelowa
5 kwi 22:07
Przewiduje pokój: a2 = e *
5 kwi 22:07
Godzio:
Ale ja tego nie miałem to tak dobrze nie ma
Daj mi coś co już miałem. Ja Cię nie męczę
całkami
5 kwi 22:07
Przewiduje pokój: Miało być po świętach cyż nie ?
Czemu psujesz piękną atmosferę xD
5 kwi 22:08
Baś: No więc:
| 2px2+2px+1 | | 2px2+2px+1−2x2−2x−4+2p2 | |
| ≥2⇔ |
| ≥0 |
| x2+x+2−p2 | | x2+x+2−p2 | |
Zacznijmy od mianownika:
dla : x
2+x+2−p
2 Δ<0 ⇔ Δ=1−4(2−p
2)=1−8+4p
2=4p
2−7 <0 (2p−
√7)(2p+
√7)<0
Licznik:
mianownik >0, stąd licznik też ≥0
2px
2+2px+1−2x
2−2x−4+2p
2≥0
2x
2(p−1)+2x(p−1)+2p−3≥0
p−1>0 ⇒
(2) p>1
Δ≤0 ⇔ Δ=4(p−1)
2−8(p−1)(2p−3)=[4(p−1)(2(p−1)−8(2p−3)]=
| | 11 | |
[4(p−1)(2p−2−16p+24)]=[4(p−1)(−14p+22)]⇔ (3) p∊(−∞,1>∪< |
| ,+∞) |
| | 7 | |
ostatecznie:
| | 11 | |
wynikałoby z tego, że p∊< |
| ,+∞) |
| | 7 | |
Czyli
źle 
5 kwi 22:08
Godzio:
"Przewiduje pokój: Możesz dać"
5 kwi 22:08
Przewiduje pokój: Basia w ogóle nie uwzględnia swojego pierwszego załozenia
Ma je w pupie
5 kwi 22:10
Godzio:
Licznik, masz błąd: 2x2(p − 1) + 2x(p − 1) + 2p2 − 3
5 kwi 22:11
Przewiduje pokój: po drugie Basia nie umie wyciągać przed nawias
5 kwi 22:11
Baś: Basia idzie się pociąć.
5 kwi 22:12
Godzio:
Baś popraw błędy i podaj ten wynik !
5 kwi 22:13
Przewiduje pokój: Godziu a taka granica :
wiem że trzeba skorzystać z liczby e tylko nie wiem jak to sprowadzić do postaci z której
mógłbym skorzystać. Mógłbyś podać jakiś schemat?
5 kwi 22:13
Baś: Nienawidzę poprawiać błędów. Robię jeszcze raz
5 kwi 22:14
Przewiduje pokój: Kobieca logika...
5 kwi 22:15
Godzio:
| | n + 1 | | n + 2 − 1 | |
( |
| )2n + 3 = ( |
| )2n + 3 = |
| | n + 2 | | n + 2 | |
| | 1 | | 1 | |
= (1 − |
| )2n + 3 = [ (1 − |
| )n + 2 ](2n + 3)/(n + 2) → (e−1)2 = |
| | n + 2 | | n + 2 | |
e
−2
5 kwi 22:15
Baś: Raczej
moja logika
Czyli dość pokrętna.
5 kwi 22:16
Przewiduje pokój: | | 1 | |
[(1 − |
| n+2](2n+3)/(n+2) → e−12 ... |
| | n+2 | |
Jak?
5 kwi 22:18
Godzio:
| | 1 | |
(1 − |
| )n + 2 dąży do e−1 tak? |
| | n + 2 | |
No ale mamy jeszcze wykładnik, który dąży do 2
5 kwi 22:24
Przewiduje pokój: ... żałosny jestem...
5 kwi 22:26
Baś: Uwaga
kolejna zła odpowiedź.
To będzie jakiś 5−ty zły wynik w tym zadaniu.
Pocieszające jest, że za założenia dostałabym 1pkt
A że liczyć nie umiem..., inna bajka
5 kwi 22:30
AC:
Można skorzystać z takiego wzoru:
lima→0 (1 + a)b = elim ab
5 kwi 22:30
Godzio: Ta odpowiedź akurat jest dobra
5 kwi 22:31
Przewiduje pokój: ty pacz zrobiła xD
pewnie przepisała z wcześniejszych
5 kwi 22:31
Baś: ICSP... dopadnę Cię za tę uwagę, która była nie na miejscu.
5 kwi 22:31
Przewiduje pokój: widzisz tu gdzieś ICSP ?
5 kwi 22:32
Baś: Tak.
5 kwi 22:32
Przewiduje pokój: hmmm ja nie
Godzio, Eta, AC, Przewiduje pokój ale szanownego ICSP nie widać ...
5 kwi 22:33
Baś: Schizofrenia to dość częsta, przykra doległość.
Godzio, masz coś jeszcze?
5 kwi 22:34
Przewiduje pokój: Ja mam
5 kwi 22:35
Godzio:
Mam tysiące zadań, zaraz coś dam,
pokój zabieraj się za te zadania co Ci dałem
5 kwi 22:36
Baś: Jej... tak sobie właśnie myślę, że słowo "doległość" nie istnieje.
Matko, co mi się dzieje z
głową... Chyba za dużo snu.
Nieważne, poproszę
5 kwi 22:36
Godzio:
Łatwe zadanie, w którym jest kilka pułapek
Rozwiązać równanie:
√4x − 3 − 3 =
√2x − 10
5 kwi 22:37
Przewiduje pokój: Godziu czy ja też mogę ?
5 kwi 22:37
Godzio:
Ty masz tamte robić, chyba, że nie chcesz ?
5 kwi 22:38
Eta:
Nieeeee
bo to dla Naszej
Basiek
5 kwi 22:39
5 kwi 22:42
5 kwi 22:47
Baś: Już? ... Jej, po herbatę byłam
No to liczmy
5 kwi 22:48
AC:
Godzio patrzę na to zdanie z pierwiastkami i zastanawiam się, gdzie są te pułapki?
5 kwi 22:53
Przewiduje pokój: Ja widzę przynajmniej trzy.
5 kwi 22:53
Baś: Czy powinno mi wyjść coś... brzydkiego?
5 kwi 22:53
Przewiduje pokój: Jeśli dla ciebie liczby naturalne są brzydkie to chyba nigdy nie liczyłaś niczego wzorami
Cardano
5 kwi 22:54
AC:
Wychodzą liczby pierwsze.
5 kwi 22:54
Baś: Wyszedł mi pierwiastek? Więc liczba niewymierna, nie naturalna...
5 kwi 22:55
Baś: Suuuper
Uwielbiam się za dar liczenia. ^^
5 kwi 22:55
AC:
Ja nie widzę żadnej.
5 kwi 22:55
Przewiduje pokój: ooo
Godziu mam dla ciebie zadanko
5 kwi 22:56
Godzio: AC dla nas nie ma, ale dla ludzi którzy nie robili takich równań może być problem z
rozwiązaniem
5 kwi 22:56
ZKS:
Dobry wieczór wszystkim!
5 kwi 23:04
Przewiduje pokój: Witaj ZKS chcesz zadanko ?
5 kwi 23:18
Baś: Cześć
ZKS
Powiedzmy, ze wyszło
5 kwi 23:18
ZKS:
Można poprosić.
5 kwi 23:20
Przewiduje pokój: Już zapodaje :
Zadanie dla ZKS:
Liczba 135 ma taką własność że jeżeli podniesiemy cyfry tej liczby do kolejnych potęg
naturalnych i je zsumujemy otrzymamy właśnie tę liczbę :
11 + 32 + 53 = 1 + 9 + 125 = 135
Znajdź liczbę która ma taka samą własność i leży najbliżej liczby 135.
5 kwi 23:22
ZKS:
Może 175?
5 kwi 23:28
Przewiduje pokój: Mi też tak wyszło
5 kwi 23:29
ZKS:
Fajne zadanko.
5 kwi 23:30
Przewiduje pokój: Mogę wiedzieć jak to rozwiązałeś ?
5 kwi 23:31
Godzio: ZKS 22:04 −− jak chcesz możesz rozwiązać, bo panu
Pp się nie chciało
A ja na zadanie od
Pp czekam i czekam i się doczekać nie mogę
5 kwi 23:36
ZKS:
Szczerze mówiąc nic nie rozwiązywałem spodziewałem się że spełniać będą to liczby pierwsze. A
Ty to jakoś rozwiązałeś?
5 kwi 23:37
Przewiduje pokój: Godziu kochanie powiem ci to ostatni raz :
DOSTANIESZ SWOJĄ INDUKCJĘ W PONIEDZIAŁEK WIECZOREM NAJPÓŹNIEJ. MAMY ŚWIĘTA
DAJ ODPOCZĄĆ
5 kwi 23:37
Przewiduje pokój: za a przyjąłem liczbę 1 a później za b kolejno w górę i w dół na zmianę. Później rozwiązywałem
odpowiedni wielomian.
5 kwi 23:38
Godzio:
Ale mi miałeś jakieś zadanie dać
5 kwi 23:38
Przewiduje pokój: nie odzywałeś się to dałem ZKS. Pomyślałem że nie chcesz
5 kwi 23:39
ZKS:
Nie wiem czy i ode mnie odpowiedzi się doczekasz.
5 kwi 23:39
Baś: Jesteście obłędni.
Godzio, na pewno jesteś świadomy, że
PP się tak tylko wymiguje i przekłada terminy ;>
Ja chyba przez tą całą matematykę przerzucą się dziś na angielski
5 kwi 23:40
ZKS:
Ja przyjąłem 1 na początek i 5 na koniec bo wiadomo 3 automatycznie odpada (33 = 27).
5 kwi 23:42
Godzio:
5 kwi 23:47
ZKS:
Baś mówiłaś że kochasz analityczną więc proszę takie maturalne.
Wyznacz te wartości rzeczywiste parametru k, dla których okrąg opisany równaniem:
x
2 + y
2 + 2x − 6y + 2k − 2 = 0 jest styczny do prostej o równaniu 4x + 3y + 5 = 0.
5 kwi 23:48
Godzio: Dobra przeprowadzę dowód, bo i tak się nudzę, chyba że ...
5 kwi 23:53
ZKS:
Może nierówność Bernoulliego?
5 kwi 23:56
Baś: ZKS z dużym prawdopodobieństwem JEST źle, bo dziś jakby... nie kontaktuję, muszę się
ogarnąć
Wyszło mi k=4,5
5 kwi 23:57
ZKS:
Wiesz te pół mi tutaj nie pasuje.
5 kwi 23:58
Baś: To tak jak mnie
5 kwi 23:59
Baś: Rzućmy okiem:
(x+1)2+(y−3)2=2−2k+1+9
okrąg: (−1,3) r=√12−2k
No, ja tu oczywiście zamieniłam 1−nkę na dwójkę przy dodawani.
Założenia k<6
bla bla.
k=4
6 kwi 00:02
ZKS:
Tak mi się wydaję że lubisz połówki.
Teraz jest wszystko
.
6 kwi 00:04
Baś: Chyba pierwiastki....
to mnie wykończy
6 kwi 00:06
Baś: Mamy coś jeszcze z analitycznej?
to mnie uspokaja
6 kwi 00:08
ZKS:
Pierwiastki nie ale połówka zniszczy Ci wątrobę i wykończy.
6 kwi 00:10
ZKS:
Znajdź punkt symetryczny do punktu A = (2, 6) względem prostej o równaniu 3x + 4y − 5 = 0.
6 kwi 00:10
6 kwi 00:11
Godzio:
Pokażemy, że ciąg a
n jest ograniczony z góry i rosnący
| | | | 1 | | | | 1 | | | | 1 | |
an = 1 + | * |
| + | * ( |
| )2 + ... + | * ( |
| )n = |
| | | n | | | n | | | n | |
| | n(n − 1) | | 1 | | 1 * 2 * ... * n | | 1 | |
= 1 + 1 + |
| * |
| + ... + |
| * |
| = |
| | 1 * 2 | | n2 | | 1 * ... * n | | nn | |
| | | | | | n − 1 | | n − 2 | | 1 | | (1− |
| )(1 − |
| )...(1 − |
| ) | | | n | | n | | n | |
| |
= 2 + |
| + ... + |
| < |
| | 1*2 | | 1*..*n | |
| | 1 | | 1 | | 1 | |
< 2 + |
| + |
| + ... + |
| < |
| | 1 * 2 | | 1 * 2 * 3 | | 1 * 2 * ... *n | |
| | 1 | | 1 | | 1 | | 1 | |
< 2 + |
| + |
| + |
| + ... + |
| < 3 |
| | 2 | | 4 | | 8 | | 2n | |
Korzystamy tutaj z faktu, że n! > 2
n
Hmmm, jak pokazać, że to rośnie
?
6 kwi 00:13
Godzio: Właściwie, że n! ≥ 2n − 1 dla n ≥ 1
6 kwi 00:15
ZKS:
Mi się wydaję że to już pokazałeś że to rośnie.
6 kwi 00:18
Godzio:
Hmmm, gdzie ?
6 kwi 00:20
Baś: (−4,−4) co wydaje mi się jednakże ... złe, aczkolwiek bez połówek
6 kwi 00:24
ZKS:
| | 1 | | 1 | | 1 | |
< 2 + |
| + |
| + ... + |
| i ta suma będzie rosła do 1 |
| | 2 | | 22 | | 2n | |
6 kwi 00:24
ZKS:
Rzędna jest zła odcięta dobra.
6 kwi 00:26
6 kwi 00:27
Godzio:
No niech będzie, ale muszę to przemyśleć,
To teraz to z średnią arytmetyczną ...
a
n → a więc a
n = a + ε
n gdzie ε
n → 0 więc:
| a1 + a2 + ... + an | | a + ε1 + a + ε2 + ... + a + εn | |
| = |
| = |
| n | | n | |
| | ε1 + ε2 + ε3 + ... + εn | |
= a + |
| , przechodząc do granicy wyrażenie: |
| | n | |
| ε1 + ... + εn | |
| dąży do 0, więc wynikiem jest to co chcieliśmy otrzymać czyli a. |
| n | |
6 kwi 00:28
ZKS:
Baś nie licz dalej.
6 kwi 00:31
Baś: Mam 3 różne wyniki
To jest nieogarnięte
6 kwi 00:32
ZKS:
Podpowiem że powinna Ci wyjść liczba całkowita.
6 kwi 00:36
Baś: punkt A' znajduje się na prostej
4x−3y+10=0
czyli dla x=−4
4*(−4)−3y+10=0
−16+10−3y=0
−6=3y=> y=−2
Może mi ktoś wyjaśnić, dlaczego nie umiałam tego policzyć?
6 kwi 00:37
ZKS:
I teraz jest
.
6 kwi 00:43
Baś: Chociaż dalej nie wiem, czemu wektorami wychodzi mi źle
wektory AB=BA'
| | 4x+10 | |
dla A(2,6) B(−1,2) A'(x, |
| ) |
| | 3 | |
| | 4x+10 | |
[−3,−4]=[x+1, |
| −2] |
| | 3 | |
x=−4
−6=4x+10
−16=4x
x=−4
...
6 kwi 00:47
kylo1303: Pozwole sobie włączyc sie w dyskusje. Staram sie aktualnie nadrobic zadanka podane przez was.
Poki co mam te:
(rownanie z pierwiastkami 22.37)
x=7 v x=13
Zadanie z prawdopodobienstwa z tematu "
https://matematykaszkolna.pl/forum/138188.html" wyszlo mi n=6, czyli wszystkich kul bylo 2n=12 (to
zadanko co pytal
Przewiduje pokój
Zaraz policze z punktem symetrycznym oraz z parametrem p.
6 kwi 00:48
Godzio:
Wynik 7 i 13 jest ok
6 kwi 00:52
kylo1303: A'=(−4,−2)
6 kwi 00:52
Baś: Tak właśnie patrzę. Patrzę. I w swojej jasności umysłu policzyłam dwa razy iksa. I wielce
zdziwiona, że wyszło źle kilka razy pod rząd. Sama ze sobą nie wytrzymuję
Za dużo snu mam,
szkodzi mi
6 kwi 00:54
kylo1303: Co do tego zadania mam pytanie (sry ze w oddzielnym poscie, za szybko kliknalem), albo moze i 2
pytania:
1. do Baś
"4x−3y+10=0
czyli dla x=−4"
Skad wiesz ze masz wybrac x=−4 ?
2. Ja to obliczalem z odleglosci punktow (rownanie prostej prostopadles, obliczam odleglosc
punktu A i przyrownuje do odleglosci punktu A' od prostej−symetralnej). Nie wiem czy jest to
najszybszy sposob, bo wspomniane zostaly rowniez wektory. Ktos kto ma za duzo czasu moglby
napisac pokrotce kroki rozwiazywania? (nie chce na nowo robic zadania, zajmie sie kolejnymw
tym czasie)
6 kwi 00:55
Baś: Bo
ZKS powiedział mi, że to dobrze obliczyłam
Też liczyłam równanie prostej prostopadłej, punkt wspólny, a potem z wektorów. Bardzo okrężna
droga, ale zawsze, kiedy mam okazję przypomnieć sobie równania prostych w postaci ogólnej−
robię to, bo nigdy nie pamiętam
I wektory− bo uwielbiam
6 kwi 00:58
ZKS:
Dla każdego n ∊ N, wyrazy ciągu (a
n) spełniają dwa warunki:
| | −n2 + 3n + 17 | |
an + an + 1 = |
| |
| | n2 + 1 | |
i
| | 6n + 19 | |
an − an + 1 = |
| . |
| | n2 + 1 | |
Oblicz, które wyrazy tego ciągu są dodatnie.
6 kwi 01:00
Godzio:
Nie no, to chyba już za łatwe
6 kwi 01:01
Godzio:
n ∊ {4,5,6,7,8,9,10,11} hm ?
6 kwi 01:03
Baś: Miałam to bodajże na maturze próbnej
6 kwi 01:04
ZKS:
Niestety nie.
6 kwi 01:05
Godzio:
Czyli zbyt banalnie to potraktowałem
6 kwi 01:06
ZKS:
Nie no banalne jest w pamięci można nawet zrobić.
6 kwi 01:07
kylo1303: Z okregiem wyszlo mi dobrze. Z parametrem p nie chce mi sie liczyc. Z tym punktem A i
symetralna to moznaby chyba latwiej znalezc punkt przeciecia prostych i potem liczyzc ze
srodka odcinka
Jak na swieta (w najblizszych dniach) nigdzie nie jedziecie to bym moze kiedys poprosil was o
jakies zadanka z dowodow geometrycznych (planimetria i stereometria) bo na dobra sprawe te 2
dzialy musze ostro przecwiczyc do maturki. Z arkuszy maturalnych OE co 3cie zadanie z tych
dzialow nie bardzo chce mi wyjsc lub wychodzi wymeczone.
Dacie jeszcze jakies ostatnie zadanko przed spaniem? tylko zeby obliczenia byly w miare (zeby
sie nie zmeczyc
)
6 kwi 01:10
kylo1303: Odpowiedz do ciagow to: n∊{1,2,3} ?
6 kwi 01:12
ZKS:
Można było ze środka odcinka właśnie to policzyć też zadanie.
6 kwi 01:13
ZKS:
Kurde myślałem że proste dałem no chyba że ja się gdzieś walnąłem idę jeszcze raz sprawdzić.
I
kylo1303 zła odpowiedź.
6 kwi 01:15
rumpek:
| | −n2 + 3n + 17 + 6n + 19 | | −n2 + 9n + 36 | |
2an = |
| = |
| |
| | n2 + 1 | | n2 + 1 | |
mianownik jest zawsze dodatni, zatem wystarczy rozpatrzyć tylko licznik:
−n
2 + 9n + 36 > 0
Δ = 81 + 144 = 225
n
2 − 9n − 36 < 0
(n + 3)(n − 12) < 0
Czyli n∊{1,2,3,...,11} [bo tylko wartości dodatnie z przedziału (−2,12)
Tak może na odchodne
6 kwi 01:15
6 kwi 01:17
kylo1303: no tak... taki maly minusik w mianowniku mi umcknal przez co moje rownanie mialo postac:
(n−3)(n+12)<0
Zmeczenie
6 kwi 01:18
ZKS:
rumpek git.
6 kwi 01:19
Godzio:
Ja za to miałem dobrze, ale źle odczytałem
6 kwi 01:20
ZKS:
Wierzę Ci na słowo.
A teraz
Godzio zadanko dla Ciebie:
Znajdź równanie krzywej którą tworza wszystkie punkty jednakowo odlegle od prostej x = 3 i
punktu A = (0 ; 0).
6 kwi 01:27
Godzio:
Elipsa za pewne
Ale zaraz Ci wyliczę
6 kwi 01:28
ZKS:
Nie elipsa.
6 kwi 01:29
Baś: Ja wiem, ja wiem !
Parabola
ma ognisko i kierownicę
6 kwi 01:30
Godzio:
B(x,y)
Odległość punktu od prostej: d
1 = |x − 3|
Odległość od punkt A: d
2 =
√x2 + y2
d
1 = d
2 /
2
x
2 − 6x + 9 = x
2 + y
2
No popatrz, jednak parabola
6 kwi 01:30
Godzio:
Coś jednak umiem
kierownica: x = 3
ognisko: F(0,0)
6 kwi 01:33
ZKS:
No
Baś ładnie a skąd wiedziałaś robiłaś kiedyś takie zadanie?
Godzio oczywiście
dobrze.
6 kwi 01:34
Baś: Nie, po prostu kiedyś musiałam coś takiego przeczytać/ usłyszeć. Jesli dobrze kojarzę,
Eta
coś takiego kiedyś napisała. Mignęło mi przed oczami. Takie dziwne rzeczy zdarza mi się
zapamiętać.
Chyba pouczę się tego z wikipedii
Podoba mi się.
6 kwi 01:36
Godzio:
Jak chcesz mogę Ci napisać na szybko def. z parabolą, chyba że chcesz coś więcej ;> ?
6 kwi 01:38
Baś: Dawaj.
6 kwi 01:39
ZKS:
Polecam książkę "Tablice Matematyczne" Wydawnictwa "Podkowa" tam to wszystko o wszystkim jest
super napisane sam się uczyłem z tej książki.
6 kwi 01:40
6 kwi 01:41
Godzio:
Def. Parabola: {P ∊ R
2: |PF| = d(P,k)}
Oznaczenia: F − ognisko, k − kierownica, 2p − parametr paraboli
2p = 2d(F,k) = 2|FO| (odległość ogniska od kierownicy)
W(x
0,y
0) −− wierzchołek paraboli
Fakt: Niech 2p będzie parametrem, W(x
0,y
0) wierzchołkiem paraboli, której oś symetrii jest
równoległa do osi OX. Wtedy równanie paraboli ma postać:
(y − y
0)
2 = 2p(x − x
0)
| | p | | p | |
k: x = x0 − |
| , F(x0 + |
| , |
| | 2 | | 2 | |
6 kwi 01:43
ZKS:
Tylko zobaczyła byś ją a od razu zmieniła byś zdanie.
6 kwi 01:44
Godzio:
Baś ja niedługo wprowadzam w czyn mój plan nauki
Podręczniki zakupiłem i planuje teraz
się przyłożyć, bo jeśli nie będę naprawdę dobry to nie bd mógł zostać na uczelni
6 kwi 01:45
Godzio:
| | p | |
yyy, F(x0 + |
| ,y 0) |
| | 2 | |
6 kwi 01:45
ZKS:
Baś a ile miejsc zerowych ma ta parabolka?
6 kwi 01:47
ZKS:
Ojj ja tak sobie mówię i mówię że muszę się wziąć za naukę fizyki i jakoś mi to nie idzie.
6 kwi 01:48
Godzio: Dobrze, że ja fizykę mam za 2 lata
6 kwi 01:49
Godzio:
ZKS co ostatnio przerabiacie na analizie ?
6 kwi 01:50
ZKS:
Całki podwójne i potrójne obliczanie pól i objętości.
6 kwi 01:50
Baś: Boże. Skomplikowane. Dużo wzorów, faktów.
Godzio dostajesz zakładkę
Chłopcy... wiecie, ja za jakieś 20kilka dni maturę piszę
Uświadomiłam sobie, że moje wzniosłe
plany i tak nic nie dadzą i chyba sobie po prostu poodpoczywam
, Wy się uczcie. Wiecie−
kwiat młodzieży polskiej i takie tam
6 kwi 01:51
Godzio:
Łojej, to zanim my do tego dojdziemy to już końcówka roku będzie o ile w ogóle zaczniemy
6 kwi 01:51
ZKS:
Fizyka jak fizyka ale laborki z fizyki to jest ...
6 kwi 01:52
Godzio:
Ja nie wiem, nie czytam Sienkiewicza ani Mickiewicza
6 kwi 01:52
ZKS:
Ostatnio mieliśmy koło z funkcji wielu zmiennych (pochodne , ekstrema , itp).
6 kwi 01:53
Godzio:
Beznadziejne programy macie, omijają was najfajniejsze rzeczy z matematyki
6 kwi 01:54
ZKS:
Kiedy będziesz miał teraz
Godzio więcej wolnego czasu?
6 kwi 01:54
6 kwi 01:54
Godzio:
Po 18 kwietnia, i gramy
Wtedy mam ostatnie kolokwium
6 kwi 01:55
Godzio:
To właściwie jedyna rzecz, którą umiałem z Dziadów, bo pisaliśmy z niej arkusz, dostałem
bodajże 32%
6 kwi 01:56
ZKS:
My to mamy umieć i rozumieć bez dowodzeń i dlatego szybko idzie i sporo omijamy no nie raz
jakieś dowodzenie się zdarzy.
A co takiego ciekawego mnie omija?
6 kwi 01:57
Godzio:
Za pewne szeregi
6 kwi 01:57
ZKS:
Ja to pamiętam najbardziej Kordiana jak mnie tą książką nauczycielka męczyła.
6 kwi 01:58
Baś: ZKS− ukradłam z internetu tę książkę. Tam masa wiadomości jest z poziomu studiów (lub do
starej matury), czy mi się wydaje?
6 kwi 01:59
ZKS:
Szeregi miałem razem z ciągami i granicami.
6 kwi 02:01
ZKS:
A jest dużo ale bardzo ciekawie napisane. Zobacz strona 93 jest ta parabolka.
6 kwi 02:02
Godzio:
No coś ciekawego na pewno pomijacie, dowody nie zajmują nam całego wykładu
6 kwi 02:03
ZKS:
Promocja jest Powrót do Karkrand kosztuje chyba 25zł więc zakup sobie hehe.
6 kwi 02:04
Baś: "mimośród paraboli"? O.o
I co to jest w końcu ten parametr p?
6 kwi 02:05
ZKS:
A Ty czym teraz się zajmujesz na matematyce?
6 kwi 02:05
Godzio:
Musiałbym zajrzeć do wykładów, ale mimośrodu chyba nie ma w paraboli hmmm
6 kwi 02:07
Baś: Tak tu jest napisane.
Cóż ja poradzę?
6 kwi 02:08
6 kwi 02:09
Godzio:
Nie wiem jak wy, ale ja padam i idę spać, także dobranoc
6 kwi 02:24
Baś: Śpię co prawda 18/24, ale pewnie masz rację. O 6−tej pobudka.
Dobranoc i dzięki z a wszystko
6 kwi 02:25
ZKS:
Dobranoc.
I też idę na spanie.
6 kwi 02:28
