ciagi joe: http://www.zszmatema.yoyo.pl/ciagi.pdf Prosze o odp. do tych zadan z ewentualnych wyliczeniem , jak co oblicza sie zeby wynik wyszedl.

do M.: No, ale zamknięte to już chyba sobie poradzisz..

joe: niekoniecznie..

baranek chwalipięta :D: 1. Poczytaj sobie o ciągach. <−− tu z boku, bo i tak nie zrozumiesz co napiszę. Pokażę jedno za 2pkt. 1)

	a1 + an
Sn =		* n
	2

S_n = 1650 a₁ = 250 a_n = (a₁ + (n − 1)(−20))

	250 + 250 − 20n + 20
1650 =		* n
	2

3300 = 520n − 20n² −20n² + 520n − 3300 = 0 Dalej równaniem kwadratowym. Wyjdą dwa rozwiązania. Jedno odrzuć, pomyśl dlaczego

baranek chwalipięta :D: Te zadania są pewnie, żebyś się nauczył. Ja ew. mogę pomóc, naprowadzić, a pewnie nie wiesz nawet o co cho.

joe: w tym 1 odp. 11 rat.

joe: a w tym 2 jak?

baranek chwalipięta :D: Tak, a dlaczego druga odp. odpada?

baranek chwalipięta :D: Drugie. Napisz wzór na sumę w ciągu geometrycznym. S_n = a₁ = 500

	4
q =
	5

n = 4 Podstaw i oblicz.

joe: bo kwota raty zjechala by do minusowej

baranek chwalipięta :D: Świetnie. Zrób drugie.

joe: odp w ciagu czterach dni przejechal 1476km.

baranek chwalipięta :D: Świetnie. Takie trudne? A wiesz, skąd n, q oraz a₁?

joe: tak. a teraz prosze o pomoc w 3.

baranek chwalipięta :D: Jaka zależność zachodzi w ciągu geometrycznym? [patrz ciąg geometryczny z boku]

joe: a2a1

baranek chwalipięta :D: 279 na samym dole , własność

joe: czyli a² = ¹₄ (a + 3) ?

baranek chwalipięta :D: Tak.

joe: i jak wyliczyc a jezeli a² = ³₄a ?

baranek chwalipięta :D: a² ≠ 3/4 a a² = 1/4a + 3/4

joe: aha, i jak teraz?

baranek chwalipięta :D: Dalej, Δ i równanie kwadratowe.

joe: aha to licze.

joe: a = 1 ¹₄, 1 , 4

baranek chwalipięta :D: Ok.

joe: a w 4 co trzeba wykorzystac?

baranek chwalipięta :D: Z: n² − 5n − 8 = 6 Przerzuć −6 i delta itd.

joe: ok

joe: a₇ = 6

baranek chwalipięta :D: świetnie ]]... Takie złe?

joe: teraz te trudniejsze za wiecej pkt.....

baranek chwalipięta :D: Zerkne czy potrafię

baranek chwalipięta :D: Robimy I.

joe: ok!

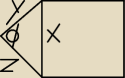
baranek chwalipięta :D: Mamy: x możemy obliczyć Skoro pole kwadratu x² = 100, to x = 10 Mamy x. W tr. prostokątnym musi zachodzić zależność y² + z² = x² W ciągu arytmetycznym:

	x + z
y =
	2

Podstaw to co masz i rozwiąż ten układ równań.

baranek chwalipięta :D: Rozumiesz?

joe: cos mi nie chwychodzi w ukladzie

baranek chwalipięta :D: y² + z² = 10²

	10 + z
y =
	2

10 + z
	2 + z2 = 100
2

100 + 20z + z2
	+ z2 = 100 *4
4

100 + 20z + z² + 4z² = 400 5z² + 20z − 300 = 0 Dalej Δ itd.

baranek chwalipięta :D: Wracając do początku.. jeżeli czegokolwiek nie rozumiesz PISZ Chodzi aby zrozumieć, a nie rozwiązać

joe: y=8 x=10 z=6 (6,8,10) ciag arytemtyczny i teraz obliczyc pole trojkata...

baranek chwalipięta :D: To już banalne

joe: P = 24

baranek chwalipięta :D: Ok. następne.

baranek chwalipięta :D: Spróbuj sam. Zapisz dane najpierw.

joe: S_n = 440 r = 1 a_n = 35 ?

baranek chwalipięta :D: Ok. Przyjmijmy, że a₁ = x Napisz wzór na: a) A_n b) S_n CIĄG ARYTMETYCZNY, gdyż dodajemy cały czas to samo.

joe: Sn = a1 i an2 * n

baranek chwalipięta :D: a a) a_n?

joe: a_n = a₁ + (n−1)r

baranek chwalipięta :D: Ok. Podsumujmy co mamy: S_n =440 r = 1 a_n = 35

	a1 + an
Sn =		* n
	2

a_n = a₁ + (n − 1)r Do tych wzorów podstawiamy dane:

	a1 + an
Sn =		* n
	2

a_n = a₁ + (n − 1)r

	a1 + 35
440 =		* n
	2

35 = a₁ + (n − 1) * 1

	a1 + 35
440 =		* n
	2

35 = a₁ + n − 1 ⇒ a₁ = 35 − n + 1 ⇒ a₁ = 36 − n

	a1 + 35
Podstaw a1 do 440 =		* n i oblicz dalej.
	2

joe: a₁ = 36 − n

baranek chwalipięta :D: Podstaw a₁ do wzoru i oblicz do końca. Potem Δ itd. i wyjdzie n = ileś

joe: licze licze

joe: n₁ = 16 n₂ = 55

baranek chwalipięta :D: n₂ wykluczamy, gdyż a₁ ≠ −19

baranek chwalipięta :D: Mamy n − ilość rzędów. Oblicz a₁ (ilość miejsc w pierwszym rzędzie) podstawiając n do wzoru.

joe: a₁ = 20

baranek chwalipięta :D: Świetnie. Sprawdź czy a₁₂ pomieści 30 osób [Takie jest pytanie]

joe: w kazdym rzedzie powieksza sie o 1 miejsce tak?

joe: wiec a₁2 = 31 , wiez zmiesci sie 30 osob

joe: * a₁₂ = 31

baranek chwalipięta :D: Napisz odpowiedź pełnym zdaniem i koniec

baranek chwalipięta :D: 3. W miarę proste. Dawaj Co wiesz.

joe: wiem w sumie jak sie robi , tylko te liczby potrzebne mi sa 3 pierwsze i ostatnia

baranek chwalipięta :D: Dwucyfrowe: 7n + 3 a₁ = 7n + 3 = 10 a₂ = 7n + 3 = 17 a_13ostatni = 7n + 3 = 94 Policz dalej. Podaj wynik

joe: ok, ale o co chodzi z ta reszta jak zostaly znalezione te liczby?

baranek chwalipięta :D: Po co ? Z ciągów. Sumę z ciągów obliczysz , gdyż trzeba zawuażyć, że kolejne liczby 10,17,24 tworzą ciąg arytmetyczny o r=7.

joe: S₁₃ = 676

baranek chwalipięta :D: Yeah.

baranek chwalipięta :D: Nast. Mamy liczby: 1 __ __ 10 1 x y 10 1 x y <−−− tw. ciąg geom. x y 10 <−−− tw. ciąg arytm. Wypisz własności z obu ciągów i użyj do podanych wyżej liczb

joe: no to jeszcze tak szybko te 4 i sie zmywam ( reszte zadan rowniez dokoncze w tym temacie)

baranek chwalipięta :D: Pozostałe podobnie jak poprzednie.. 5−7. Powinienies sobie poradzić . Jak cośt napisz..

joe: to jak to obliczyc w tym 4 , bo mam malo czasu ?

baranek chwalipięta :D: x² = 1 * y <−−własność c. geom.

	x + 10
y =		<−−− własność c. aryt.
	2

Podstawiasz y do pierwszego potem delta, bla bla bla

joe: delta wyjdzie w przylizeniu?

joe: * przyblizeniu

baranek chwalipięta :D: nie .. √Δ = 9

joe: to cos mam zle w rachunkach

joe: nie wiem ciagle mi wychodzi delta 164 .......

baranek chwalipięta :D:

	x+10
x2 =		*2
	2

2x² = x + 10 −2x² + x + 10 = 0 ... Δ = 1² + 4 * 10 * 4 = 81

joe: juz wiem

joe: x = 2,5

joe: y = 6,25

joe: (1; 2,5 ; 6,25; 10) taki ciag wyszedl , dobrze?

baranek chwalipięta :D: Tak... A ogólnie te ciągi są trudne dla ciebie?

joe: raczej mam problem zawsze z rozpoczeciem zadania itd. dalej jakos leci. ok, dziekuje za pomoc w zadaniach, jeszcze sie w tym temacie odezwe, jak nastapia jakies trudnosci z dalszymi zadaniami,

baranek chwalipięta :D: Jasne

joe: Prosze o pomoc w 5, 6 i 7 z zadan rozszerzonej odpowiedzi

joe: ?

tim: Witam ponownie

Basia: 5. (4 pkt) W ciagu geometrycznym drugi wyraz jest równy 6, a piaty wyraz jest równy 48. Oblicz, ile wynosi pierwszy wyraz, iloraz oraz suma wyrazów tego ciagu od piatego do dziesia− tego. a₂ = 6 a₅ = 48 a₂ = a₁*q a₅ = a₁*q⁴ a₁*q = 6 a₁*q⁴ = 48 rozwiąż ten układ równań, wylicz a₁ i q a₅ + a₆ + ...... + a₁₀ = S₁₀ − S₄

	1−qn
Sn = a1*
	1−q

oblicz S₁₀ i S₄ a potem ich różnicę

Basia: 6. (4 pkt) Za trzy płyty, których ceny tworzą ciąg geometryczny zapłacono 142,50 zł. Najdroż− sza z nich kosztowała o 7,50 zł mniej niż dwie pozostałe razem. Oblicz, ile kosztowała każda z płyt. c₁,c₂,c₃ ciąg geometryczny rosnący o wyrazach nieujemnych c₁+c₂+c₃ = 142,5 c₃ = c₁ + c₂ − 7,5 c₁+c₂+c₃=142,5 c₁+c₂−c₃ = 7,5 −−−−−−−−−−−−−−−−−−−−−−−−−− 2c₁ + 2c₂ = 150 c₁ + c₂ = 75 75 + c₃ = 142,5 c₃ = 67,5 −−−−−−−−−−−−−−−−−−− c₁*q² = 67,5 c₁ + c₁*q = 75 rozwiąż ten układ równań

Basia: 7 . (3 pkt) Suma n kolejnych początkowych wyrazów ciągu arytmetycznego wyraża się wzorem Sn = 3n² − 13n. Wyznacz wzór ogólny na n−ty wyraz tego ciągu. a_n = S_n − S_n−1 S_n−1 = 3(n−1)² − 13(n−1) = 3(n² − 2n + 1) − 13n + 13 = 3n² − 19n + 16 podstaw do pierwszego za S_n i za S_n−1, zredukuj wyrazy podobne