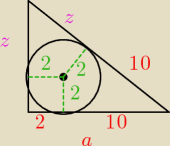
okrąg wpisany w trójkąt asdf: a = 12 r = 2 −−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−− Skorzystałem tutaj z tw. pitagorasa, i wyszło mi, że z = 3. Da się to zrobić innym sposobem? z tw.pitagorasa: (z + 2)² + 12² = (z + 10)² (......) −16z = −48 z = 3

Artur z miasta Neptuna: https://matematykaszkolna.pl/strona/542.html

	2P		12*(2+z)
r =		⇔ 2 =		⇔ z = ...
	a+b+c		24+2z

asdf: dzięki

pigor: ... lub r = ¹₂(a+b−c) = ¹₂(12+5−13) =2 . ...

asdf: pigor, tylko z kąd Ci wiadomo, że jest to trójkąt o takich wymiarach? Też wiedziałem, że tak będzie, ale trzeba to jakoś udowodnić

Artur z miasta Neptuna: pigor ... akurat z tego nic nie wynika:

1		1
	(12 + (2+z) − (10+z)) =		(12+2−10) ... więc 'z' nie wyliczysz
2		2

pigor: hmm ... sprawa jest prostsza niż myślisz − zresztą nie tylko ty , bo z własności stycznych do okręgu : (a−r)+(b−r)=c ⇔ a+b−c = 2r. .. i tyle . ...

pigor: ... przepraszam, ale ja myślałem, że chodzi wam skąd ten mój wzór na r , a co do zadania wolałbym widzieć jego treść, a nie sam rysunek .. no to z mojej strony tyle,

Artur z miasta Neptuna: pigor ... ale Ty nie masz obliczyć 'r' tylko długości boków trójkąta a konkretniej 'z'

asdf: Na okręgu o promieniu 2 opisano trójkąt, gdzie jedna z przyprostokątnych = 12. Oblicz obwód(zrobili obwód, żeby wyznaczyć miary boków trójkąta, które wyznaczyłem, tylko chciałem wiedzieć czy jest jakiś inny sposób na to). W skrócie, a = 12, r = 2 + rysunek (pierwszy post)