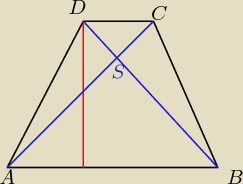
zadanie Kaśka: Punkt S jest punktem przecięcia się przekątnych trapezu ABCD. Pole trójkąta ABS jest równe 9, natomiast pole trójkąta CDS wynosi 4. Oblicz pole trapezu ABCD, wiedząc, że jego wysokość poprowadzona z wierzchołka C na podstawę AB ma długość równą 10. Proszę o pomoc

Kaśka: potrafi mi ktoś pomóc

Maciek: halo jesteś?

Kaśka: tak jestem

Aga1: P_ABS=P₁=9, P_CDS=P₂=4 P_trapezu=(√P₁+√P₂)²=(3+2)²=25

Eta:

Kaśka: Pierwszy raz spotykam się z takim wzorem i nie mogę go ogarnąć

Eta: https://matematykaszkolna.pl/forum/133835.html Zobacz tu ( masz uzasadnienie )

Eta: To bardzo przydatny i elegancki wzorek

rumpek:

Kaśka: No teraz to rozumiem Bardzo dziękuję

Kaśka: W szkole nam go nie podali, więc nie wiedziałam że tak wzór istnieje

Eta: Można też tak: k >0 −−− skala podobieństwa trójkątów ABS i CDS

	P(ΔABS)		9		3
zatem:		= k2 ⇒ k2=		⇒ k=
	P(ΔDCS)		4		2

taki wzorek: P(tr) = (k+1)²*P(ΔCDS)

	5
to: P(tr)= (		)2*4= 25
	2