Prawdopodobieństwo Basiek: Wydaje się ambitne. Może ktoś się skusi. W urnie znajduje się N losów, przy czym M z nich to losy wygrywające (M≤N). Wybieramy losowo n losów z urny (n≤N) i niech p oznacza prawdopodobieństwo, że dokładnie , m spośród losów to losy wygrywające (m≤M oraz m≤n). Uzasadnij, że:

	n m   N−n M−m   *
p=
	N M

elpe: ja Ci to pięknie zrobie a Ty mi napisz list z angliczka

Basiek: To co to tam potrzebujesz?

elpe: a działasz coś z Longmana podst. ?

Basiek: Nie, ale posiadam.

elpe: to mozesz mi pomóc bezinteresownie bo prawdopodobieństwa jeszcze nie potrafie na takim poziomie ja tam dopiero urny/kuleczki orzeł\reszka

Basiek: Haha No mogę, mogę

elpe: 14 dział Państwo i społeczeństwo list do redakcji. napisalem niby to ale nie czuje zeby ta praca była za rewelacyjna zwłaszcza ze pisałem o murzynach wykorzystywanych w kopalni I would be grateful

Basiek: Jesteście przy 14−tce? wooow. My ostatnio pisaliśmy (ja nie przyszłam) spr z 7−mki i 8−mki.

elpe: no jesteśmy skończymy to i mamy robić do końca same matury ustne z jakiejś tam książki

Basiek: Hm, może mi podasz jaki chcesz problem opisać, dlaczego jest istotny, jaka jest przyczyna itd? 5 zdań po polsku o czym mam pisać

rumpek: elpe masz to Repetytorium z Longmana, podstawowe?

elpe: no więc ja osobiście napisałem o tych biednych "nigger" wśród których mam kolegę wykorzystywanego w pracy w kopalni pracuje 2x dłużej za 0,5 wynagrodzenia przypuszczalną przyczyną jest nieznajomość prawa (w sensie czarni nic nie wiedzą) a rozwiazanie problemu nagłosnienie przez media i edukacja jeżeli nie masz czasu to nie pisz bo źle sie bd z tym czuł mozemy tez zrobic tak: dokończę swoja prace i wyśle Ci na e−mail to mi sprawdzisz bo na forum zdjecia nie wrzucę

elpe: tak na tym opiera sie moja wiedza Longman..

Basiek: Szczerze mówiąc, tak byłoby najlepiej. Mam problem z wymyślaniem. Potłumaczyć mogę, gramatykę uwielbiam robić, ale zmyślać... no, problematyczne.

rumpek: też to mam dopiero 9 unit zaczęliśmy (kulturę)

elpe: no to rumpek nie matematyka tylko mozesz zrobić wyjątek i mi napisać

Basiek: My jesteśmy przy zdrowiu, jedenastce. A w drugiej grupie (rozszerzenie) są przy 10−tce: nauka i technika. Od zeszłego tygodnia chodzę na 2 angielskie ^^

rumpek: u mnie ang wygląda tak, że na rozwiązywanie ćwiczeń przeznaczamy 1−2h lekcyjne a przez kolejny tydzień pyta każdego z tego materiału ustnego (ale rzecz jasna nie na ocenę)

Basiek: My mamy na zadanie domowe prawie cały dział, który potem drugi raz robimy na lekcjach. ...

elpe: no to my pierwsze 10ćwiczeń do domu 1 lekcja czytanie 2 słuchanie 3 pytanie losowe 1 os 4 kartkówka ze słówek i pisanie podobnego listy czy coś czasem 3 x 2

rumpek:

Basiek: My mamy spr. z dwóch działów, z czego jest tam może 10−15 słowek (czyli średnio się opłaca uczyć), opis obrazka, jakieś pytania, coś jakby z ustnej, ale pisemnie i jest napisanie listu. A w domciu nic nie piszemy W ogóle, robię tego Longmana tylko dlatego, że obiecałam kolegom, żeby mieli od kogo przepisać. Mam za dobre serce

rumpek: a co ty tam z tym listem wyskrobałeś ?

elpe: nadal skrobie wstawię poźniej wersję finalną, może Wam sie przyda

Basiek: Pisz, pisz Rumpek mógłbyś coś przeanalizować i mi wytłumaczyć? Takie proste coś.

rumpek: co takiego na razie oglądam skoki a potem będę maturkę sprawdzał

Basiek: http://www.zadania.info/d38/2128188 Obliczyłam i nie zgadza mi się z tym wynik, jak chciałam sobie sprawdzić. Robiłam tym pierwszym sposobem. Wychodzi : m∊(−∞,−1)∪(1,+∞) (po uwzględnieniu i odjęciu opcji f. liniowej)

	4
I jeszcze trzeba porównać warunek z Δ => m∊(−∞,−		>∪<0,+∞)
	5

Jakim cudem komuś wyszła taka odp? −₋

rumpek: Tym ich pierwszym sposobem to:

⎧	x1 + x2 ≥ 0
⎩	x1 * x2 ≥ 0

takie warunki + Δ ≥ 0 Warunki gwarantują nam, że pierwiastki będą nieujemne, czyli dodatnie + zero. Rozwiązując te warunki otrzymamy m∊<−1,1) <− czyli ta odpowiedź to dla czego są nieujemne (dodatnie + zero). Pozostało narysować sobie całą sytuację, czyli taką aby otrzymać pierwiastki niedodatnie (ujemne + zero), wystarczy wyciąć z liczb rzeczywistych ten przedział i otrzymamy: x∊(−∞, −1)U<1, +∞) potem tylko część wspólna i otrzymamy rozwiązanie

rumpek: pomarańczowe − nieujemne, czerwone − niedodatnie(tych szukamy)

Basiek: Ruuumpek ukatrupię Cię Dotąd rozumiem. Tylko potem, jak już CI to wyjdzie i porównasz sobie to z dziedziną....

	4
nie powinno wyjść czasem m∊(−∞,−		>∪(1,+∞)
	5

rozumiesz... to −4/5 z Δ ,...

rumpek:

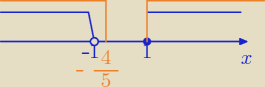
rumpek: dobrze jest

Basiek: A widzisz, kto by pomyślał, że −4/5 jest bliżej 0 niż taka −1. Bo na pewno nie ja.

rumpek: zawsze najłatwiej narysować i zaznaczyć

Basiek: Ależ rysowałam.

rumpek:

Basiek: Pozostawmy to bez komentarza. Idę na kawę. Potrzebuję odpoczynku. Będę za godzinkę. Rumpku dziękuję. Elpe, będę na forum za godzinkę, ale jak coś: basiek@gg.pl − mój mail

Aga1:

	N n
1)IΩI=

	M m	N−M n−m
IAI=

	IAI
P(A)=
	IΩI

p=P(A) jak się rozpisze lewą i prawą stronę, to ładnie wychodzi bez żadnego kombinowania.

Basiek: Aga dziękuję, doszłam do tego, żeby to tak przedstawić, ale nie bardzo umiem przekształcić lewą do prawej. Ale dziękuję bardzo, będę próbować. PS. Jakby coś, to ja już jestem

elpe: aa za zaraz Ci wysle na maila to mi sprawdzisz te "głupoty" to moze nawet oddam prace i dostanę 5

Basiek: Okeeej

Basiek: Wykaż, że jeżeli trójkąt nie jest rozwartokątny, oraz miara α jednego z jego kątów spełnia

	2cos2α
warunek sinα+cosα≤		to trójkąt ten jest prostokątny.
	sin2α−2

Oo

Aga1: Odnośnie zadania z prawdopodobieństwa. Basiek Przekształć lewą i prawą stronę i zobaczysz, że są równe.

Basiek: Aguś chwilka, bo jestem w środku jeszcze innego zadanka. Zaraz będę próbować

Basiek: Na pewno nie ma ktoś jakiegoś super pomysłu do udowodnienia tego czegoś o trójkącie, żebym mogła to chociaż wykuć na pamięć?

Godzio: Momencik

Basiek:

Basiek: To ja idę po kawę

Godzio: Informacja, że trójkąt nie jest rozwartokątny mówi nam, że cosα,sinα > 0 i α ∊ (0^o,90^o) Zatem: (sin2α − 2)(sinα + cosα) − 2(cos²α − sin²α) ≥ 0 (2sinαcosα − 2)(sinα + cosα) − 2(cosα − sinα)(cosα + sinα) ≥ 0 (sinα + cosα)(2sinαcosα − 2 − 2cosα + 2sinα) ≥ 0 (sinα + cosα)(2cosα(sinα − 1) + 2(sinα − 1) ) ≥ 0 2(sinα + cosα)(sinα − 1)(cosα + 1) ≥ 0 Na początku mamy dane, że ta nierówność jest prawdziwa, zatem: sinα + cosα > 0 (to wiemy z założenia) sinα − 1 ≥ 0 ⇒ sinα ≥ 1 ⇔ sinα = 1 ⇒ α = 90^o cosα + 1 > 0 Zatem trójkąt jest prostokątny

Basiek: Jezu, Godzio, a coś Ty zrobił w pierwszej linijce, że masz zwykłą nierówność bez pierwiastków?

Basiek: * bez ułamków. Ech, naprawdę padam jak rzadko.

Godzio: Pomnożyłem przez (sin2α − 2) pamiętając o zmianie znaku nierówności i odjąłem to co po prawej zostało

Basiek: Okej, jak będziesz potrzebować nerki, to daj znać.

Godzio: Haha Ok

Basiek: Nawet zrozumiałam O.o Jeszcze 5 zadań i mogę iść spać

Godzio: To ja dalej czytam opowiadanie po niemiecku

Basiek: Niemiecki... fuu. Powodzenia. I dziękuję. Bardzo, bardzo, baaardzo.

Basiek: Ma ktoś jeszcze czas/ siłę przemęczyć ze mną jedno zad. z wektorami?

Godzio: No dawaj, a nie się pytasz

Basiek: W czworokącie ABCD dane są wektor AB = [6,−3], wektor DA = [−8,−7] oraz środek S = (3, 2) przekątnej DB. Wyznacz współrzędne rzutu prostopadłego punktu D na prostą AB.

Basiek: I ten... bo jakby nie wiem, co robię źle.

Basiek: (tu wektory) BD=DA+AB= [−2,−10]

1
	BD= BS= SD =[−1,−5]
2

Basiek: z tego : 3−x_b=−1 2−y_b=−5 B(4,7) x_d−3=−1 y_d−2=−5 D(2,−3) I teraz.... bo to D powinno mieć współrzędne B .

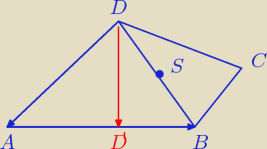
Godzio: Rysunek to podstawa i teraz mogę myśleć

Basiek: Potrzebne mi tylko do wyliczenia pkt A, B, D. W sumie, wiem jak zrobić, ale za nic mi nie wychodzi. Wychodzi na opak...Przez co

	185
D'(1		,y).....
	389

Godzio: Masz odp ?

Basiek: http://www.zadania.info/8185465

Godzio: Tak mi wychodzi

	22		111
D'(		,
	13		13

Basiek: A jaki D Ci wychodzi?

Godzio: S(3,2) Pierwsze już masz źle, bo DB = DA + AB = [−2,−10] DB = DS + SB ⇒ DS = SB = [−1.−5] x_B − 3 = − 1 ⇒ x_B = 2 y_B − 2 = − 5 ⇒ y_B = − 3 3 − x_D = − 1 ⇒ x_D = 4 2 − y_D = − 5 ⇒ y_D = 7 B(2,−3) D(4,7) AB = [6,−3] ⇒ 2 − x_A = 6 ⇒ x_A = − 4, −3 − y_A = −3 ⇒ y_A = 0 A(−4,0) Prosta AB: −3 = 2a + b 0 = 4a + b −3 = − 2a

	3
a =
	2

	3
b = − 6 y =		x − 6
	2

Prostopadła przechodząca przez D :

	2
7 = 4 * (−		) + b
	3

	29
b =
	3

	2		29
y = −		x +
	3		3

Punkt przecięcia:

	2		29		3
−		x +		=		x − 6 /* 6
	3		3		2

− 4x + 58 = 9x − 36 13x = 22

	22
x =
	13

	33		111
y =		+ 6 =
	13		13

Szukaj błędu Współrzędne wyliczyłem dobrze i wgl hmmm

Basiek: Dodawanie wektorów było ponad 2 lata temu. Widzę, że oczywiście źle. Jak zawsze na początku. Jej.... mało skoczyć z mostu. Dobra, rozkminię te wszystkie zad. chociażbym miała nie spać i jutro do szkoły nie wstać. A Ty powinieneś dostać jakiś order

MQ:

	1
Jeżeli AB=[6,−3] to w prostej AB wsp. a=−
	2

Godzio: Zapamiętaj: AB + BC = AC a B znika

Eta: Zamiast "orderu" ......... dla Godzia

Godzio: No już znalazłem ... 3 = 2a + b 0 = −4a + b 3 = 6a

	1
a=
	2

Basiek: Jakieś nowatorskie metody nauki widzę. Ja jednak wolę "początek z początkiem, koniec z końcem" I jest wektor!

Eta: Jak w życiu ............. związać koniec z końcem

Godzio: Hehe

Eta:

Basiek: I rozwiązać matematykę z poniedziałkiem. Dałam się wmanipulować w robienie wszystkim zadań, przez co własnych... nie zrobiłam. Dobra, liczę/ przepisuję/ myślę!

kylo1303: Widze, ze niektorzy za nic maja pozna pore Ja tez postanowilem sobie zrobic caly zestaw z Aksjomatu (geometria analityczna) i wlasnie udalo mi sie skonczyc. Przy czym sprawdzajac jedno zadanie natknalem sie na twoj watek Basiek (128448) i powiem szczerze ze strasznie sobie utrudniliscie z rumpkiem zadanie Mnie naszly watpliwosci czy mam dobrze bo nie skorzystalem w ogole z informacji, ze trojkat jest rownoboczny, a mimo to bylo banalne (proste dzialania na wektorach). Wiec jak bedziesz miala troche czasu wolnego to polecam powrocic do zadania i sprobowac dzialan na waktorach, bez obliczania wspolrzednych wierzcholka C To tak w ramach treningu.

Basiek: Jak wyłączę gg i facebooka, to będę mieć mnóstwo wolnego czasu. PS. nienawidzę wektorów. I wiesz co kylo? Ty to potrafisz wbić nóż prosto w serce.

MQ: Basiek błąd jest na początku! DA+AB to jest DB, a nie BD, stąd ci wyszły błedne współrzędne punktów B i D. A potem już poleciało.

kylo1303: W tym momencie ranisz moje uczucia. Ja to wszystko z myśla o Tobie! Trafi ci sie takie zadania na maturze to zamiast 3min bedziesz robic 15 Po zrobieniu zestawu musze stwierdzic ze w geo. analitycznej jest jeden wielki plus: zadania mozna czesto zrobic na kilka sposobow. Kiepsko tylko jak wybierzesz ten zly (raz obliczenia zajely mi pol strony A4, i byly typu: √121104, a mozna bylo to zrobic w 2och linijkach− tak wiec wiem cos o zlym doborze sposobu rozwiazywania)...

Basiek: Ale: "Po 2. chciałam sobie poćwiczyć z tym wykorzystaniem tg, bo hm... rzadko korzystam, a okazuje się przydatne." Zresztą− nienawidzę wektorów

Basiek: Reasumując zrobiliśmy− bo ja to raczej średnio 21 zadań z matury rozszerzonej na takim dość wysokim, tak mi się zdaje poziomie. Nieukończone zostało tylko jedno. Ale to nic. Dziękuję. Dobranoc