prawdopodobieństwo całkowite,wzór Bayesa iwa: W magazynie znajdują się żarówki pochodzące z dwóch fabryk. 6% pochodzi z fabryki I. Wśród żarówek z fabryki I jest 1 % wadliwych, a spośród żarówek z fabryki II 2 % wadliwych. Z magazynu pobrano losowo jedną żarówkę , która okazała się wadliwa. Jakie jest prawdopodobieństwo tego,że ta żarówka została wyprodukowana przez fabrykę II?

Artur z miasta Neptuna: wykorzystaj wzór na prawdopodobieństwo warunkowe: https://matematykaszkolna.pl/strona/1020.html gdzie: A − żarówka pochodzi z fabryki I B − żarówka jest zepsuta A∩B − żarówka pochodzi z fabryki I i jest zepsuta

Patronus: I − wybór pierwszej fabryki, P(I) = 0,06 II − wybór drugiej fabryki P(II) = 0,94 W − wybór wadliwej żarówki P(W) = 0,06*0,01 + 0,94*0,02 = 0,0194 II∩W − wybór wadliwej żarówki z II fabryki P(II∩W) = 0,94*0,02 = 0,0188 Prawdopodobieństwo, że żarówka pochodzi z II fabryki, pod warunkiem że jest wadliwa:

	0,0188
P(II/W) = U{P(II∩W)}{P{W}) =		= 0,969072165
	0,0194

iwa: Dziękuję

A: To jest źle wyliczone.Prawdopodobieństwo powinno wynieść 0,571

PW: @A. co ty mówisz? Na zdrowy rozum: gdyby wadliwość była jednakowa, to prawdopodobieństwo, że wadliwa pochodzi z fabryki drugiej wynosiłoby 0,94 (bo taka jest procentowa zawartość wyrobów z tej fabryki w magazynie). Wadliwość wyrobów z drugiej fabryki jest jednak większa niż z pierwszej. Szukane prawdopodobieństwo musi być większe niż 0,94, tak więc wynik Patronusa jest rozsądny, a Twój nie.

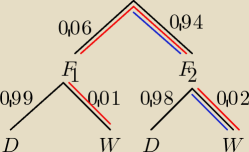
Gustlik: W magazynie znajdują się żarówki pochodzące z dwóch fabryk. 6% pochodzi z fabryki I. Wśród żarówek z fabryki I jest 1 % wadliwych, a spośród żarówek z fabryki II 2 % wadliwych. Z magazynu pobrano losowo jedną żarówkę , która okazała się wadliwa. Jakie jest prawdopodobieństwo tego,że ta żarówka została wyprodukowana przez fabrykę II? I to jest typowe zadanie na drzewka. Prawd. całkowite wylosowania żarówki wadliwej: P(W)=0,06*0,01+0,94*0,02=0,0194 P(W|F₂)=0,02 − to można odczytać z drzewka, Ze wzoru Bayesa:

	P(W|F2)*P(F2)		0,02*0,94
P(F2|W)=		=		=0,969
	P(W)		0,0194

Czyli stosując wzór Bayesa możemy podzielić odnogę drzewka, która nas interesuje (zaznaczona na niebiesko przez prawdopodobieństwo całkowite.