Badanie zmienności funkcji [wykres funkcji]
DeCoo: Witam, proszę o pomoc w badaniu zmienności funkcji x2−4x/x−2
Pierwsza pochodna wyszła mi: −16, czyli brak ekstremów
Druga pochodna wyszła mi: 2, z tym że 2 nie należy do dziedziny (i co dalej?)
Asymptota pionowa w punkcie 2
Asymptota ukośna y=x−2
Nie umiem wykonać wykresu tej funkcji (chodzi mi o zaznaczenie asymptot, ekstremów, punktów
przegięcia itd).
Pomoże ktoś?
Proszę...
17 lut 14:53
think: zacznijmy od tego, że pierwsza pochodna na pewno nie będzie miała wartści liczbowej, ponieważ
chociażby pochodna z x
2 to jest 2x i w dodatku pewnie nie skorzystałeś ze wzoru na pochodną
ilorazu...
17 lut 16:07
17 lut 16:08
DeCoo: | x2−4x | |
| −> o tak, źle napisałem. |
| x−2 | |
17 lut 16:16
Aga1: Już miałam pytać, czy aby dobrze przepisałeś., bo od tego trzeba zacząć..
17 lut 16:17
DeCoo: Przepraszam za pomyłkę

17 lut 16:19
Aga1: Już w pierwszej pochodnej mi się nie zgadza.
17 lut 16:19
DeCoo: | | x2−4x+8 | |
znaczy 1 pochodna wychodzi: |
| , czyli przyrównuje do 0 i wtedy liczę deltę. |
| | (x−2)2 | |
i wtedy delta wynosi −16.
I jak to wtedy zaznaczyć na wykresie?
17 lut 16:24
Aga1: Dziedzina D=R−{2}
Pochodna dobrze obliczona.
Pochodna nie ma miejsc zerowych, więc funkcja nie ma ekstremum.
f'>0⇔ x∊R−{2}
Funkcja jest rosnąca w przedziałach (−∞,2), (2,∞).
Trzeba jeszcze policzyć granice.
17 lut 16:30
DeCoo: czyli asymptota pionowa = x=2
a ukośna y = x−2
Tak mi wyszło.
I teraz nie wiem jak to zaznaczyć na wykresie...

17 lut 16:37
Aga1: Asymptota pionowa zgadza się,
Mi wyszło, że nie ma asymptoty ukośnej.
Zapisz swoje obliczenia.
17 lut 16:41
Aga1: Oblicz miejsca zerowe funkcji. i narysujemy wykres ( bez drugiej pochodnej)
17 lut 16:43
DeCoo: okej, chwilka

17 lut 16:55
Aga1: Ale teraz już nie mam czasu, jak nie dasz rady, to pomogę Ci później.
17 lut 17:01
DeCoo: teraz mi coś inaczej wychodzi :
| | x2−4x | | x2−4x−2x2+4x | | −x2 | |
lim |
| − 2x = lim |
| =lim |
| = i co teraz? |
| | x−2 | | x−2 | | x−2 | |
Miejsce zerowe wyszło 4.
17 lut 17:01
DeCoo: Byłbym bardzo wdzięczny, jeżeli jescze dzisiaj, bo od tego zależy moja dalsza przyszłość

17 lut 17:02
DeCoo: Punkt przecięcia z osią OX to (4,0) , z OY (0,0)?
Funkcja jest rosnąca w przedziałach (−∞,2), (2,∞). −> jak to policzyłaś?
17 lut 17:43
Aga1: I granica tego wynosi −∞, przy x →∞ więc b nie istnieje.Reszta zgadza się
Jeśli jesteś to zapisz wszystkie granice (początek i koniec.)
Jak wszystko dobrze wyliczone, wykres to bajka.
17 lut 17:51
DeCoo: to tak:
1) Dziedzina (−
∞,2)(2,
∞)
| | x2+4x+8 | |
2) I pochodna: |
| |
| | (x−2)2 | |
3) Asymptota pionowa: x=2
4) Asymptota ukośna: y=x−2 bo:
| x2−4x | | 1 | | x2−4x−x(x−2) | | x2−4x−x2+2x | | −2x | |
| * |
| = |
| = |
| = |
| = |
| x−2 | | x | | x−2 | | x−2 | | x−2 | |
17 lut 18:08
DeCoo: To jest dobrze, tak?
Hm właśnie o to chodzi, że dla mnie nie bajka, nie potrafię tego zrobić

17 lut 18:09
Aga1: Ale nie zapisałeś tego , o co Cię prosiłam.
I asymptoty poziomej nie ma, bo a=−2, a b wyszło∞
17 lut 18:10
Aga1: Chciałam napisać,że asymptoty ukośnej brak.
17 lut 18:11
Aga1: lim x→−∞f(x)=−∞ tak?
17 lut 18:13
DeCoo: Hm już Ci piszę, a ty jeżeli byś mogła to zobacz te b u mnie, u mnie coś tak nie wychodzi

17 lut 18:14
DeCoo: lim x→−∞f(x)=−∞ −> z tym zapisem Ci chodzi o to, ile mi wyszło przy liczeniu asymptoty ukośnej?
(przy dzieleniu funkcji przez x?)
17 lut 18:15
Aga1: Więc wykres będziemy zaczynać rysować od lewego dolnego rogu, funkcja przechodzi przez punkt
(0,0) i jest rosnąca (−∞, 2)
Prosta x=2 jest asymptotą pionową, więc wykres nie może przeciąć tej prostej , ale będzie się
do niej przybliżać, bo limx→2−f(x)=∞.
Kończymy tę część wykresu wysoko blisko tej prostej.
Narysuję ten fragment, a na drugim rysunku drugą część.
17 lut 18:21
DeCoo: Czy po przyrównaniu II pochodnej do 0 Tobie też x=2? Jeżeli on nie należy do wykresu to jest
brak punktów przegięcia?
17 lut 18:21
Aga1:
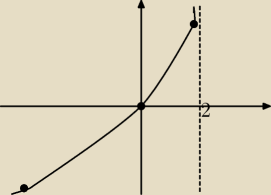
17 lut 18:23
DeCoo: Dziękuję

I to już wszystko zaznaczone?
Hm, a czy na pewno nie ma tej ukośnej? Bo wpisałem na stronie wolframaplha i mi też policzyło,
że jest ukośna y=x−2
17 lut 18:26
Aga1: Teraz limx→2+=−∞
Funkcja jest rosnąca, więc zaczynamy rysować od dołu, oczywiście po prawej stronie prostej x=2
Miejscem zerowym jest 4, wicć wykres przecina oś x w (4,0)
limx→∞f(x)=∞, więc kończymy rysunek w prawym górnym rogu.
17 lut 18:28
DeCoo:
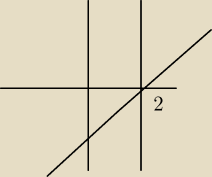
To nie będzie coś takiego?
I teraz trzeba zaznaczyć reszte, ale nie mam pojęćia jak
17 lut 18:29
Aga1:
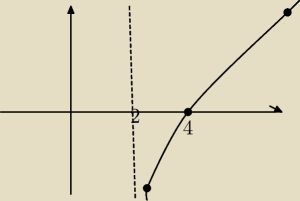
17 lut 18:31
Aga1: Teraz te dwa rysunki trzeba narysować na jednym układzie współrzędnych.
A odnośnie tej asymptoty to jeszcze sprawdzę,
Być może, ze się pomyliłam.
17 lut 18:33
DeCoo: Jak Ci wyszedł punkt 4?
funkcje zrównałaś do 0?
a wtedy nie wyjdzie x2=4x czyli x=2 lub x=−2?
17 lut 18:34
Aga1: O 17:01
próbowałeś obliczyć b do asymptoty poziomej i pytałeś co teraz?
17 lut 18:36
DeCoo: o 18.08 to policzyłem (tam masz jak po kolei liczyłem asymptotę ukośną)
17 lut 18:37
Aga1: x2−4x=0
x(x−4)=0
x=0 lub x=4.−−−to są miejsca zerowe.
17 lut 18:37
Aga1: Ale a=−2,
b=limx→∞(f(x)−ax)
17 lut 18:39
DeCoo:
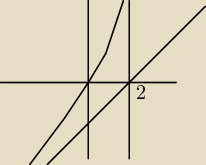
to wychodzi coś takiego?
i teraz ze strony prawej asymptoty się rysuje, tak?
17 lut 18:40
DeCoo: znaczy a= 1
b = −2
czyli równanie to y=x−2
tak?

17 lut 18:41
DeCoo: Hm nie wiem czy nie mieszam, ale miejsca zerowe to nie mianownik =0?
17 lut 18:42
DeCoo: jednak masz racje, bo x
2−4x=0
więc potem x(x−4)=0
więc x=0 albo x=4
sorka

17 lut 18:45
Aga1: Licznik przyrównałam do zera, bo mianownik 0 być nie może.
A gdzie masz wyliczone a, a gdzie b, bo nie widzę.
17 lut 18:48
DeCoo:
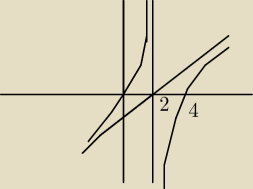
Tak to będzie wyglądać, prawda?
17 lut 18:50
DeCoo: znaczy asymptotę ukośna liczylem tak
a to funkcja/x
b to funkcja −ax
i a mi wyszło 1
natomiast b wyszło mi tak jak o godzinie 18.08 −> czyli −2
17 lut 18:51
17 lut 18:54
DeCoo: dokładnie z tego korzystałem
a wychodzi 1 (tutaj się zgadzamy tak?)
i zobacz o godzinie 18.08 mój wpis (tam masz policzone "b" w asymptocie ukośnej)
17 lut 18:55
Aga1: Już widzę, bo napisałeś dwa w jednym.
Super narysowałeś.
Wszystko jasne?
17 lut 18:57
DeCoo: Wykres jest dobry czy to ironia?

Muszę przynieśc zrobiony przebieg tej funkcji + 5 wybranych(już je mam i na 100% dobrze

),
żeby zaliczyć matme na 3

17 lut 18:58
Aga1: Dobry, oczywiście na kartce zrobisz to ładniej, można jeszcze parę punktów obliczyć.
Pytałam, czy zrozumiałeś moje wyjaśnienia.
Jeśli wszystko jest dobrze obliczone to wykres sam się rysuje.
17 lut 19:02
DeCoo: tak na kartce ładniej

po prostu po lewej stronie tylko będzie u mnie przechodzilo przez 0 i
się zbliżało do asymptoty pionowej i ukośnej, a po prawej stronie będzie przechodziło przez 4
i zbliżało się do ukośnej i pionowej

Dziękuję bardzo

jesteś wielka

17 lut 19:06
Aga1: Powodzenia.
17 lut 19:07
DeCoo: Dziękuję jescze raz

Dzięki Tobie zdam

17 lut 19:07
Aga1: Co studiujesz?
17 lut 19:08
DeCoo: Budownictwo
17 lut 19:10
DeCoo: a ty? jesteś studentką czy już nie?

17 lut 19:10
Aga1: Poszukuję pracy.
17 lut 19:14
DeCoo: Hmm, no to życzę powodzenia

A udzielasz korepetycji?
17 lut 19:15
Aga1:
17 lut 19:17







 I to już wszystko zaznaczone?
Hm, a czy na pewno nie ma tej ukośnej? Bo wpisałem na stronie wolframaplha i mi też policzyło,
że jest ukośna y=x−2
I to już wszystko zaznaczone?
Hm, a czy na pewno nie ma tej ukośnej? Bo wpisałem na stronie wolframaplha i mi też policzyło,
że jest ukośna y=x−2
 To nie będzie coś takiego?
I teraz trzeba zaznaczyć reszte, ale nie mam pojęćia jak
To nie będzie coś takiego?
I teraz trzeba zaznaczyć reszte, ale nie mam pojęćia jak

 to wychodzi coś takiego?
i teraz ze strony prawej asymptoty się rysuje, tak?
to wychodzi coś takiego?
i teraz ze strony prawej asymptoty się rysuje, tak?


 Tak to będzie wyglądać, prawda?
Tak to będzie wyglądać, prawda?
 Muszę przynieśc zrobiony przebieg tej funkcji + 5 wybranych(już je mam i na 100% dobrze
Muszę przynieśc zrobiony przebieg tej funkcji + 5 wybranych(już je mam i na 100% dobrze  ),
żeby zaliczyć matme na 3
),
żeby zaliczyć matme na 3
 po prostu po lewej stronie tylko będzie u mnie przechodzilo przez 0 i
się zbliżało do asymptoty pionowej i ukośnej, a po prawej stronie będzie przechodziło przez 4
i zbliżało się do ukośnej i pionowej
po prostu po lewej stronie tylko będzie u mnie przechodzilo przez 0 i
się zbliżało do asymptoty pionowej i ukośnej, a po prawej stronie będzie przechodziło przez 4
i zbliżało się do ukośnej i pionowej  Dziękuję bardzo
Dziękuję bardzo  jesteś wielka
jesteś wielka 
 Dzięki Tobie zdam
Dzięki Tobie zdam 

 A udzielasz korepetycji?
A udzielasz korepetycji?