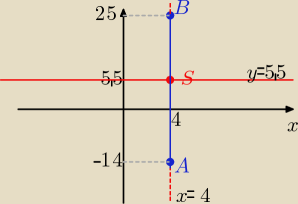
geometria analityczna makta : 2)Wyznacz równanie osi symetrii odcinka AB a) A(4;−14), B(4;25)

gauspn: 1.Wylicz równanie prostej przechodzącej przez te dwa punkty, obliczając współczynnik kierunkowy i wyraz wolny i podstaw do wzoru 2.Wylicz środek odcinka na podstawie punktu A i B Ponizej masz strone gdzie wytłumaczone jak to zrobić https://matematykaszkolna.pl/strona/1750.html 3.Wyznacz prostą prostopadłą do tej prostej przechodzącą przez punkt (środek) który wylcizyłes. Zaraz policze i podam wynik.

A ku ku: Prosta zawierająca odcinek AB ma równanie : x=4

	1
to oś symetrii odcinka AB ma równanie y= yS ⇒y= 5
	2

	yA+yB		1
bo yS=		= 5
	2		2

gauspn: Ok 1.Prosta na której zaznaczono nasz odcinek AB ma równanie x=4 2.Środek odcinka jest równy współrzędnej x=4, y=5,5 3.Jak można zauważyć prosta prostopadła przechodząca przez środek odcinka(czyli nasza oś symetrii) w punkcie y=5,5 jest funkcja stałą, a więc każdy argument (oś x−ów) ma wartość y=5,5 zatem, co jest równaniem osi symetrii, zatem odpowiedź do zadania to y=5,5.

A ku ku:

gauspn: Widzę, że byłeś trochę szybszy, dobrze że zrobiłeś rysunek, powinno to pomóc koledze jeżeli ma jeszcze jakieś wątpliwości.

A ku ku: