dowody geometryczne BLAZEJ_505: poszukuję jakiś prostych dowodów geometrycznych. ma ktoś może jakieś?

Artur z miasta Neptuna: np. Udowodnij, że przeciwległe kąty czworokąta wpisane w okrąg są sobie równe. Udowodnij, że sumy przeciwległych boków czworokąta opisane na okręgu są sobie równe

Artur z miasta Neptuna: Udowodnij, że środek okręgu opisanego na trójkącie prostokątnym, jest w połowie przeciw prostokątnej

Artur z miasta Neptuna: Udowodnij "1−nkę trygonometryczną" Udowodnij wzór na sin 2α = 2sinαcosα

BLAZEJ_505: dziękuję bardzo, postaram się to udowodnić w ramach ćwiczeń, bo nienawidzę dowód geometrycznych

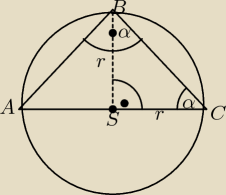
BLAZEJ_505: zacznę od 3 dowodu zał: to rysunek teza: środek okręgu jest wyznaczony na połowie przeciwprostokątnej dowód: ΔSBC− trójkąt prostokątny o kątach 45,45,90 ΔASB− analogicznie ramiona tych trójkątów to promienie okręgu IBCI i IABI=r√2 IACI=x stosując twierdzenie pitagorasa w Δ ABC, wynika (r√2)²+(r√2)²=x² x=2r co należało dowieść

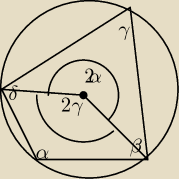
BLAZEJ_505: dowód pierwszy 2 Założenie to rysunek teza: α=γ i β=δ dowód 2γ+2α=360 α+γ=180 kąt α jest zależny od kąta γ i odwrotnie− sprzeczność z tezą, analogicznie dwa pozostałe kąty, zatem dowód jest fałszywy

BLAZEJ_505: trygonometrii na pewno nie zrobię bo tego czegoś jeszcze nie przerabiałem

BLAZEJ_505: a ten 2 dowód na czym się opiera?

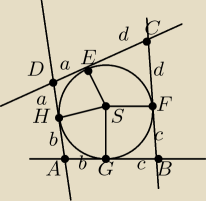
BLAZEJ_505: Założenie to rysunek Teza IABI+ICDI=IDAI+IBCI dowód czworokąt SEHD jest deltoidem, analogicznie SGAH i SGFB i SECF b+c+d+a=c+d+a+b jest to tożsamość co kończy dowód

BLAZEJ_505: mógłby ktoś to sprawdzić

Mila: Zobacz na INFO zadania dla szkoły średniej.

b.: ad 3 (@16:43): ,,trójkąt prostokątny o kątach 45,45,90'' −− nie było nic mowy o tym, że kąty ostre mają miary 45^o... ,,ramiona tych trójkątów to promienie okręgu '' −− to jest część tezy, nie możesz z tego korzystać w dowodzie!

b.: @17:46 jest dobrze (można by dokładniej uzasadnić, czemu SEHD jest deltoidem, albo lepiej czemu SE=EH oraz DE=DH).

b.: @17:11: teza jest fałszywa, a dowód fałszywości niewystarczający

BLAZEJ_505: właśnie dlatego chcę poćwiczyć dowody

BLAZEJ_505: a i dzięki za stronę Mila

al: udowodnij, że kwadrat wysokości opuszczonej na przeciwprostokątną jest równy iloczynowi dlł.odcinków, na które ta wysokość podzieliła przeciwprostokątną.

BLAZEJ_505: poddaję się, brak pomysłów

al: z podobieństwa trójkątów najłatwiej z Pitagorasa trochę obliczeń

BLAZEJ_505: jest to dowód na 2 linijki dosłownie ^a_h=^h_b h²=ab co należało dowieść

al:

BLAZEJ_505: to zarzuć jeszcze jednym dowodem na dobranoc

BLAZEJ_505: ma ktoś jakiś pomysł na dowód?

Basiek: http://matematyka.jaworzno.edu.pl/images/banners/zadania.pdf Miłej zabawy.

al: udowodnij, że w trójkącie prostokątnym suma przyprostokątnych równa się sumie średnic okręgu wpisanego i opisanego.

BLAZEJ_505: zadanie 1 IAEI=a a=¹₃IABI 3a=IABI− analogicznie pozostałe boki skoro IEBI=2a IFEI=a to zauważamy właściwości trójkąta 30,60,90 zatem ∠EFB jest prostokątny− analogicznie pozostałe co kończy dowód

BLAZEJ_505: moje zadanko na dobranoc zostało zrobione, jutro pomęczę się z innymi, dziękuję bardzo wszystkim którzy poświęcili mi czas

BLAZEJ_505: zadanie 6 z niebieskiego linku Założenie rysunek IABI=a IBSI=x IDCI=c teza IMD| + |MS| = |AB| Dowód korzystam z zależności trójkąta 45,45,90 i z podobieństwa trójkątów ΔABC, ΔBMS, ΔMDC, zatem IBCI=a√2 IBMI=x√2 IMCI=a√2−x√2=c√2→c=a−x a−x+x=a a=a co należało dowieść

BLAZEJ_505: zadanie 21 z linku założenie: a≠0 b≠0 a+b≠0 ^a_a+b=¹_√3 Teza: ^b_a+b=^3−√3₃ dowód metodą nie wprost załóżmy że teza jest fałszywa ^b_a+b≠^3−√3₃ 3b=3a+3b−a√3−b{3} a+b≠^3a_√3 sprzeczność z założeniem, zatem dowód jest prawdziwy. Co kończy dowód. Może ktoś to sprawdzić?

BLAZEJ_505: proszę bardzo

Mila: Pożyteczne! Wykazać, że w trójkącie prostokątnym suma przyprostokątnych jest równa sumie średnic okręgu opisanego na tym trójkącie i okręgu wpisanego w ten okrąg.

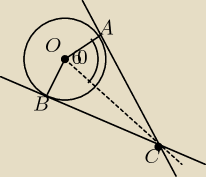
BLAZEJ_505: zadanie 30 z linku założenie rysunek IOAI=r ∡BOA=120 Teza IOCI=2r dowód ∡BOA=120 to ∡COA=60 − odcinek IOCI dzieli ∡BOA=120 na dwie równe części korzystam z zależności trójkąta 30, 60, 90 w Δ AOC IOCI=2r co należało udowodnić

BLAZEJ_505: moje dowodzenie leży i kwiczy

BLAZEJ_505: może ktoś sprawdzić te wymęczone dowody, bardzo proszę

BLAZEJ_505: ponawiam prośbę

Basiek: Problem w tym, że u mnie dowodzenie leży i kwiczy z całą planimetrią, więc raczej naprawdę nie bardzo

BLAZEJ_505: widzę że nie jestem sam

Basiek: No niestety

Basiek: Ale wiesz co? Jak dochodzisz do właściwej tezy, to pewnie jest ok. Jak sądzisz? Ja tak zawsze zakładam

BLAZEJ_505: to zależy jaka metoda

BLAZEJ_505: bo jeśli jest to dowód nie wprost to dochodzisz do sprzeczności

Basiek: Prawda dlatego, dowodów nie wprost nie lubię i raczej nie stosuję

BLAZEJ_505: to zależy jak nam matematyca mówiła że najlepszym sposobem odwodu na próbnej maturze był właśnie dowód nie wprost, tam było takie zadanie na potęgach, coś o udowodnieniu że jedna liczba jest większa od drugiej

Basiek: To zadanie z tej poznańskiej?

BLAZEJ_505: tak

BLAZEJ_505: Uzasadnij że 61¹⁶<18²⁴

Basiek: https://matematykaszkolna.pl/forum/118543.html 23:03 18 stycznia Ety rozwiązanie= 2 linijki.

Basiek: * 1 linijka. Pozdrów Panią Matematyczkę

BLAZEJ_505: szukam tego dowodu jak znajdę to go przedstawię

Eta:

BLAZEJ_505: znalazłem Teza: 61¹⁶<18²⁴ Dowód metodą nie wprost załóżmy że teza jest fałszywa, wówczas 61¹⁶≥18²⁴ (61²)⁸≥(18³)⁸ obustronnie pierwiastkujemy pierwiastkiem 8 stopnia I61²I≥I18³I pod wartościami bezwzględnymi są wartości dodatnie więc możemy je opuścić 61²≥18³ 3721≥5832 sprzeczność, zatem teza jest prawdziwa, czyli 61¹⁶<18²⁴ co należało udowodnić

Też chcę inny nick! : Eta przed kim się ukrywałaś?

Też chcę inny nick! : A w ogóle to, dalej sądzę, że dowód w 1 linijce był: a) mądrzejszy b) prostszy c) szybszy Ale mój za to wyglądał spektakularnie

BLAZEJ_505: był to dowód za 5 punktów i zapis pewnie też był punktowany

Eta:

BLAZEJ_505: btw a ktoś może sprawdzić te dowody powyżej

Też chcę inny nick! : Za każde logiczne, dobrze rozwiązane w pełni zadanie egzaminator ma obowiązek dać Ci max punktów. Oczywiście do rozwiazania Ety trzeba byłoby dopisać na końcu, że podstawniki bla blaaa, potęgi bla blaaa , z czego wynika, że X>Y... Czyli druga linijka

BLAZEJ_505: to jak będzie z tym sprawdzeniem?

BLAZEJ_505: zlituje się ktoś nad tymi dowodami

BLAZEJ_505: i nade mną

BLAZEJ_505: widzę że nikt się nade mną nie zlituję

BLAZEJ_505: ponawiam prośbę

Mila: Błażej, nie udowodniłeś o średnicach okręgów . To naprawdę potrzebne. Dowód z potęgami może być. Możesz też badać znak różnicy − rozkładać ze wzorów skróconego mnożenia .

jarkoski: sorry ze zawracam 4 litery ale wszyscy sie tutaj skupili pomozcie mi z tym zadaniem ! proszę ! https://matematykaszkolna.pl/forum/124897.html