Proszę o szybką odpowiedz. Potrzebuje to na jutro. Natalia: Określ monotoiczność ciągu an, jeżeli an=3n+10 przez 2n+7

Mila: Czy to taki ciąg?

3n+10
2n + 7

krystek: Badasz różnicę: a_n+1−a_n

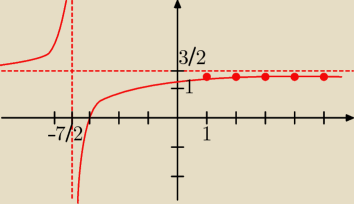
Gustlik: Lub funkcją − jest to funkcja homograficzna:

	3x+10
y=
	2x+7

3
2

−−−−−−−−−−−−−−−−−−−−−−− (3x+10):(2x+7) −3x−10,5 −−−−−−−−−−−−−−−− −0,5

	−0,5		3
y=		+
	2x+7		2

	1   −   4		3
y=		+
	7   x+   2		2

	7		3
p=−		, q=
	2		2

Na rysunku przybliżony wykres tej funkcji − hiperbola.

	3x+10
Ciąg an jest rosnący, ponieważ funkcja y=		jest rosnąca dla x∊N+.
	2x+7

Natalia: Tak, ale ja nie wiem jak się bada tą funkcję. Jak można to proszę o pomoc.

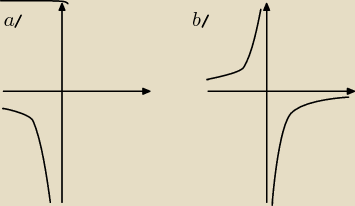
Gustlik: Funkcja homograficzna w najprostszej postaci ma taki wzór:

	a
y=
	x

Przykłady:

	1
y=
	x

	2
y=
	x

	3
y=−
	x

	1
y=−
	2x

	1		2
Jeżeli a>0, to wykres wygląda jak na rysunku a), np. y=		, y=		.
	x		x

	3		1
Natomiast jak a<0 to wykres wygląda jak na rys. b), np. y=−		, y=−		.
	x		2x

Jest to hiperbola równoosiowa.

	a
Postać kanoniczna tej funkcji to y=		+q.
	x−p

Współczynnik p przesuwa wykres w poziomie, a q w pionie, na takiej samej zasadzie, jak pzresuwa się parabolę mając daną postać kanoniczną funkcji kwadratowej, tam wzór był taki: y=a(x−p)²+q. Polecam zajrzeć na strony: 1. Funkcja homograficzna: https://matematykaszkolna.pl/strona/2456.html 2. Hiperbola: https://matematykaszkolna.pl/strona/157.html 3. Dzielenie wielomianów − pozwala zrozumieć przekształcenie funkcji homograficznej z postaci ogólnej na kanoniczną: https://matematykaszkolna.pl/strona/107.html 4. Postać kanoniczna funkcji kwadratowej − pozwala zrozumiec przesuwanie wykresów funkcji, bo hiperbolę i inne wykresy przesuwa się wg tych samych zasad: https://matematykaszkolna.pl/strona/69.html

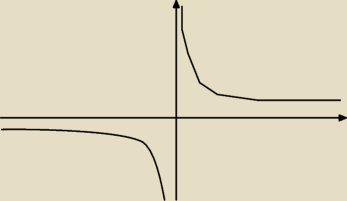
Gustlik: Poprawiam rys. a).