dany jest wielomian W(x)=(5m-6)x^4-(4m-6)x^2+m-2. Przemek: dany jest wielomian W(x)=(5m−6)x⁴−(4m−6)x²+m−2. Wyznacz wszystkie wartosci parametru m, dla ktorych wielomian ma dokladnie cztery pierwiastki

kropka: musisz najpierw rozważyć przypadek kiedy 5m−6 jest zerem i sprawdzić czy wtedy będziesz miał cztery pierwiastki czy nie , jeśli nie to wyliczone m nie spełnia warunków zdania a drugi przypadek kiedy 5m−6 nie jest równe zero tedy masz równianie czwartego stopnia z niewidomą, podstawiasz pomocniczą zmienną i rozwiązujesz równie kwadratowe które ma 2 pierwiastki żeby potem kiedy będziesz rozwiązywał z pomocniczą zmienną wyszły ci cztery pierwiastki, musisz też założyć że dwa pierwiastki równania kwadratowego nie będą sobie równe nie wiem czy wiesz o co mi chodzi, jak coś to dopytuj

Przemek: trzeba rozwiązać nierówność Δ>0?

kropka: jak już zrobiłeś pomocniczą zmienną to tak

Przemek: czyli jak wyszlo mi Δ=−m²+4m−3 to liczę Δ z tego i równanie czy jak?

kropka: masz może wynik do tego zadania?

kropka: tak wyszła Ci delta i masz założenie że jest >0 czyli −m²+4m−3>0 i rozwiązujesz

Przemek: nie, niestety nie mam. Ale jak policzylem m1=1 m2=3 to co teraz?

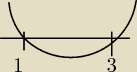
kropka: rysujesz szkic paraboli i zaznaczasz tam gdzie jest większa od zera czyli m∊(−∞;1)∪(3,+∞)

krystek: stosujesz podstawienie x²=t i t>0 i teraz aby byłt 4 pierwiastki muszą być t ₁ i t₂ dodatnie czyli z wzorów viete"a ,warunek na 2 dodatnie pierwiastki :...

kropka: jak będziesz miał rozwiązanie to napisz tutaj ja sobie sprawdzę czy dobrze bym zrobiła a ty do klasy o podst czy rozsz mat?

kropka: czyli jeszcze do tego jak napisał krystek wyżej rozważasz t₁*t₂>0 t₁+t₂>0

Przemek: i teraz się pogubiłem mam, ze m∊(1,3)/ {6/5} i jak to zapisac dalej z ta zmienna x²=t

kropka: ze wzorów Viete'a https://matematykaszkolna.pl/strona/1403.html t₁*t₂>0 t₁*t₂= ^m−2_5m−6

kropka: czy tak to rozwiązywałeś? i podobnie t₁+t₂>0 t₁+t₂=^4m−6_5m−6

kropka: po rozwiązaniu tych nierówności mi wyszły takie przedziały do pierwszego m∊(−∞;6/5)∪(2;∞) do drugiego m∊(−∞;6/5)∪(3/2;∞) i jak połączyłam wszystkie założenia to m∊(−∞;1)∪(3;∞)

krystek: 1)zał Δ>0 2)t₁+t₂>0 3)t₁*t₂>0 I ustalasz wspólny przedział dla tych trzech warunków.