funkcja kwadratowa z parametrem i wartoscia bezwzgledna Aneta321: 1. Dla jakich wartości m nierówność (m²−1)x²+2(m−1)x+2>0 jest spełniona przez każdą liczbę rzeczywistą? 2. Dla jakiej wartosci parametru m suma kwadratów rozwiazan rownania x²−(m−5)+2(3−m)=0 jest najmniejsza? 3. Rozwiąż równanie |x²−2|−|x²−9|=7 4. Rozwiąż nierówność x²−4x+|x−1|+3≤0 5. Zbadaj liczbę rozwiazan rownania |x²−2x−8|=m w zależnośći od parametru m.

Mat: Narysuj wykres funkcji I x² − 4x + 3 I = m + 2

Artur_z_miasta_Neptuna: 1. analogiczne: https://matematykaszkolna.pl/forum/155320.html

	c		−b
2. x12 + x22 = (x1+x2)2 − 2x1x2 = (		)2 − 2		ma być najmniejsza
	a		a

Mila: W drugim zadaniu, chyba czegoś brakuje. Jeśli masz odpowiedzi, to napisz. zaczynam 5)

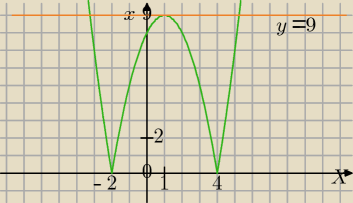
Mila: 5) |x²−2x−8|=m Rozwiązuję graficznie. f(x)=x²−2x−8 Δ=36 x−1=−2 lub x₂=4

	−b
xw=		=1
	2a

f(1)=1−2−8=−9 |f(1)|=9 1) dla m<0 brak rozwiązań 2) dla m=0 dwa rozwiązania 3) dla m∊(0;9) 4 rozwiązania 4) dla m=9 3 rozwiązania 5) dla m>9 2 rozwiązania

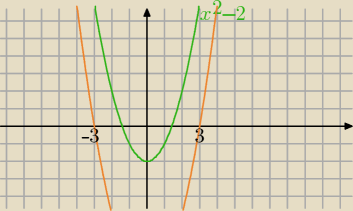
Mila: 3) |x²−2|−|x²−9|=7 x²−2≥0⇔x≥√2 lub x≤−√2 x²−9≥0⇔x≤−3 lub x≥3 1) x≤−3 (obydwie funkcje mają wartości nieujemne) x²−2−x²+9=7 7=7 równanie spełnione dla x∊(−∞,−3) 2) x>−3 i x≤−√2 x²−2−(−x²+9)=7 x²−2+x²−9=7 2x²−11=7⇔2x²=18 x=3 lub x=−3 nie należą do przedziału brak rozwiązania w tym przedziale. wysyłam. Za chwilę cd.

Mila: 3) x∊(−√2;√2) obydwie funkcje ujemne −x²+2−(−x²−9)=7 −x²+2+x²+9=7 11=7 sprzeczność, brak rozwiązań w tym przedziale 4)Teraz dokończ , tak jak Ci pokazałam.