trapez
kamil: W trapezie równoramiennym poprowadzono przekątne, dzieląc go na cztery trójkąty. Trójkąt,
którego jednym z boków jest krótsza podstawa ma pole równe 4, a trójkąt, którego jednym z
boków jest dłuższa podstawa ma pole równe 9. Obliczyć pole trapezu.
11 paź 16:24
Eta:
P
tr= 25 [j
2]

11 paź 16:27
kamil: co to jest j2
11 paź 16:29
Eta:
jednostek kwadratowych

11 paź 16:31
kamil: aha. a jak mam rozwiacac te zadanie?
11 paź 16:31
Eta:
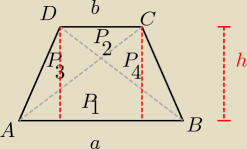
P
1=9 , P
2=4
| | a*h | |
P3=P4 bo PΔABC= PΔABD= |
| |
| | 2 | |
zatem: P
1+P
4= P
1+P
3 =>
P3=P4
P(tr)= P
1+2P
3+P
2 = (
√P1+
√P2)
2 gdzie P
3=
√P1*P2
czyli P
3=P
4=
√9*4= 6
P(tr)= P
1+ 2P
3+P
2=9+12+4= 25 [j
2]
11 paź 16:45
Eta:
Można policzyć od razu
P(tr)= (√P1+√P2)2
P(tr)=(√9+√4)2= (3+2)2= 25
przy tej okazji podałam jak obliczyć pole P3=P4 = √P1*P2= ....
11 paź 17:55
Kamcio: Eta, a czy mogłabyś napisać na jakim twierdzeniu się opieralaś? Dokładnie chodzi mi o ten
moment:
P(tr)= P1+2P3+P2 = (√P1+√P2)2 gdzie P3=√P1*P2
15 wrz 18:46
Eta:
(a+b)2=a2+2ab+b2
(√P1+√P2)2= P1+2*√P1*√P2+P2= P1+2√P1*P2+P2=P1+P3+P4+P2
2√P1*P2= P3+P4 ⇒ P3=P4= √P1*P2
15 wrz 18:51
Bogdan:
Tu jest wyprowadzenie wzoru na pole trapezu
56604
15 wrz 18:52
Kamcio: Aż mi wstyd, że nie pomyślałem o wzorze skróconego mnożenia. Dzięki uprzejmie za tak szybką
odpowiedź
15 wrz 18:53
Eta:
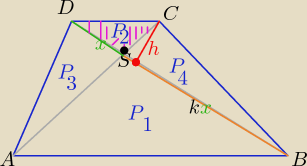
| | P1 | | 9 | | 3 | |
P2=4 , P1= 9 |
| = |
| =k2 ⇒ k= |
| , bo k>0 |
| | P2 | | 4 | | 4 | |
| | kx*h | | x*h | |
P3= P4= k*P2 ( bo P3= |
| i P2= |
| to P3= k*P2 |
| | 2 | | 2 | |
i mamy następny wzorek:
P(tr)= P
1+P
3+P
4+P
2= k
2*P
2+k*P
2+k*P
2+P
2= (k
2+2k+1)*P
2=(k+1)
2*P
2
P(tr)= (k+1)2*P2 , gdzie
P1= k2*P2 i P3=P4= k*P2
15 wrz 19:04
Eta:
| | 3 | |
Poprawiam chochlika k= |
| |
| | 2 | |
15 wrz 19:05


 P1=9 , P2=4
P1=9 , P2=4
