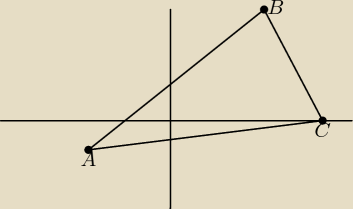
. Mańka: Sprawdź czy trójkat jest prostokątny A=(−3,−1) B=(3,4) C=(5,0). Punkt B jest środkiem odcinka CQ podaj współrzedne punktu Q. Jak narazie zrobiłam tylko rysunek, i nie wiem co dalej. Prosze o pomoc!

sushi_ gg6397228: policz dlugosci odcinkow i podstaw pod Pitagorasa 2. ze wzoru na srodek odcinka wyznaczysz pukt Q

sushi_ gg6397228: to do 1. https://matematykaszkolna.pl/strona/1248.html to do 2. https://matematykaszkolna.pl/strona/1750.html

Trivial: Ja proponuję policzyć wektory rozpinające i wziąć iloczyn skalarny dwóch par.

Mańka: Ale nie chce mi wyjsc bo jak oblicze z srodka odcinka to wyjdzie s=⁰₂ . ³₂

sushi_ gg6397228:

	xC+xQ		yC+yQ
(xB; yB)= (		,		)
	2		2

podstawic dane liczby, a potem przyrownac wspolrzedne

Mańka: dobra poddaje się, nie rozumiem

sushi_ gg6397228: masz podane wspolrzedne B i C; podstaw tam liczby

Mańka: no mam, i co dalej?

sushi_ gg6397228: to teraz przyrownaj do siebie

	xC+XQ
xB=
	2

to samo zrob z druga wspolrzedna dostaniesz wspolrzedne Q=(x_Q, y_Q) i po sprawie

Eta:

xC+xQ		yC+yQ
	= xB /*2		= yB /*2
2		2

x_C+x_Q= 2x_B y_C+y_Q= 2y_B x_Q= 2x_B−x_C y_Q= 2yB− y_C x_Q=..... y_Q=..... Nie poddawaj się dokończ ...

Mańka: Okej zrobiłam! Naprawdę wielkie dzięki, nie wiem jak mam Ci dziękować

Mańka: Mam jeszcze jedno zadanie, pomożecie?

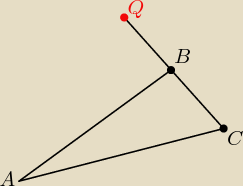
Gustlik: Sprawdź czy trójkat jest prostokątny A=(−3,−1) B=(3,4) C=(5,0). Punkt B jest środkiem odcinka CQ podaj współrzedne punktu Q. A=(−3,−1) B=(3,4) C=(5,0) I sposób − z tw. Pitagorasa: AB^→=B−A=[3−(−3), 4−(−1)]=[6, 5] → |AB|=√6²+5²=√61 AC^→=C−A=[5−(−3), 0−(−1)]=[8, 1] → |AC|=√8²+1²=√65 BC^→=C−B=[5−3, 0−4]=[2, −4] → |BC|=√2²+(−4)²=√20=2√5 Najdłuższy bok to AC, tylko on może być przeciwprostokatną. Sprawdzam tw. Pitagorasa: |AC|²=|AB|²+|BC|² 65=61+20 65=81 → trójkąt nie jest prostokątny. II sposób − iloczynem skalarnym wektorów Warunek prostopadłości wektorów: iloczyn skalarny wektorów = 0. AB^→*AC^→=6*8+5*1=48+5=53≠0, zatem wektory te nie sa prostopadłe AB^→*BC^→=6*2+5*(−4)=12−20=−8≠0, zatem wektory te nie sa prostopadłe AC^→*BC^→=8*2+1*(−4)=16−4=12≠0, zatem wektory te nie sa prostopadłe Czyli żadne dwa boki nie są do siebie prostopadłe, zatem trójkąt nie jest prostokątny.

Gustlik: ad b) A=(−3,−1) B=(3,4) C=(5,0). Punkt B jest środkiem odcinka CQ podaj współrzedne punktu Q. Q=(x, y)

	5+x		0+y		5+x		y
B=(		,		)=(		,		)=(3, 4)
	2		2		2		2

Porównujesz współrzędne i otrzymujesz:

5+x		y
	=3,		=4 → rozwiąz teraz te równania, otrzymasz współrzędne Q.
2		2

Eta: 3 sposób Gustliku

	0+1		1
aAC=		=
	5+3		8

	4+1		5
aAB=		=
	3+3		6

	0−4
aBC=		= −2
	5−3

zatem: proste zawierające boki trójkąta nie są prostopadłe => Δ ABC nie jest prostokatny Pozdrawiam

Mańka: O ile procent koła o promieniu 8 jest wieksze od pola koła wyznaczonego przez okrąg o rownaniu x²+y²−6x+5=0

Gustlik: Eta, też można, znam ten sposób "na współczynniki kierunkowe". Ale chciałem pokazać wektory i ich iloczyn skalarny, bo niestety jakiś debil wyciał je z programu na podstawach i wiele osób ich nie zna, a one są proste. Po prostu chcę zachęcić do zapoznania się z wektorami, bo one w geometrii analitycznej są niezwykle przydatne. Pozdrawiam

Eta: Pole jest większe o 1500%

Mańka: a jak to obliczyłaś?

Eta: o₂: ( x−3)²+y²=4 r²=4 dla o₁: r²=64

	64−4
		*100%=......
	4

Gustlik: O ile procent koła o promieniu 8 jest wieksze od pola koła wyznaczonego przez okrąg o rownaniu x²+y²−6x+5=0 Liczę współrzędne środka okręgu i promień: https://matematykaszkolna.pl/forum/forum.py?komentarzdo=1471 x²+y²+Ax+By+C=0

	A		−6
a=−		=−		=3
	2		2

	B		0
b=−		=−		=0
	2		2

r=√a²+b²−C=√3²+0²−5=√9−5=√4=2 Pole koła ograniczonego tym okręgiem P=πr²=4π Teraz proporcja: 4π − 100 % 8 − x %

	100*8
x=		≈63,7 %
	4π

100 % − 63,7 % = 36,3 % Wygląda na to, że pole koła o promieniu 8 jest MNIEJSZE o 36,3 % od pola koła ograniczonego tym okręgiem.

Gustlik: A,źle przeczytałem,, powinno być tak: 4π − 100 % 64 π − x %

	10064π
x=		=1600 %
	4π

1600 % − 100 % = 1500 %

Eta: @ Gustlika pole koła o promienie r=8 .... = 64π

Gustlik: Wiem, już poprawiłem przeczytałem najpierw "od koła o polu 8", stąd ta pomyłka. Tylko jeszczw wkradł sie chochlik, powinno być tak:

	100*64π
x=		=1600 %, wcisnąłem pomyłkowo potegę zamiast "*".
	4π

Eta: Gustlik .... ale się rozpisałeś a mnie to zajęło 2 niepełne linijki

Mańka: Dzięki wielkie, mam już wszystko. Strasznie jestem wam wdzięczna, dzięki jeszcze raz. Pozdrawiam

Eta: Miłych snów

Mańka: Wzajemnie!

Gustlik: Eta, nie zapomnij, że gdyby uczeń robił Twoją metodą, to miałby tyle samo linijek, co ja, bo Ty sobie w głowie zwinęłaś to wzorami skróconego mnożenia, ja też to potrafię. Ja napisałem bardziej łopatologicznie, aby Manka zrozumiała, o co chodzi, ponadto nie jestem zwolennikiem zwijania równania okręgu wzorami skróconego mnożenia, bo wielu uczniów nie rozumie metody "sztucznie dodać−odjąc" i nie wiedza, skad sie wzieły liczby, wzorami, choć może nieco wiecej linijek, to dla ucznia jest krócej w czasie, a na maturze czas jest cenniejszy od pieniądza, bo zanim uczeń zdąży wykombinować liczby, które trzeba odjąć i dodać, to wcześniej zdąży obliczyc wzorami i zabierze się za następne zadanie, zamiast ślęczeć nad liczbami.

Eta: I tu się mylisz Gustliku liczyłam tak samo: S(a,b)

	−6		0
a=		=3 b=		=0 c=5 r2=a2+b2−c= 32+02−5= 4
	−2		−2

o: ( x−3)²+y²=4 Miłych snów

Gustlik: No ale liczyłaś w głowie, nie pisałaś tego stąd mniej linijek. Niemniej większość uczniów woli pisać, no chyba że ktoś jest bardzo sprytny. Ja napisałem, żeby Mańka wiedziała, skąd to sie wzieło. Pozdrawiam