Romb xxxg: Czworokąt ABCD jest rombem. Dane są trzy wierzchołki tego rombu. B(4;−5), C(3;2), D(−2;7) a) Wyznacz współrzędne wierzchołka A. b) Napisz równanie okręgu wpisanego w ten romb.

TOmek: moj pomysł: dojdź do równania okręgu: −równanie okregu (który ma środek w miejscu przecięcia się przekątnych S(x_s,y_s), łatwo jest ten punkt wyznaczyć gdyż przekątnego w rombie są prostopadłe). I okrąg ten przechodzi przez punkt A(x_A,y_A) i C(3,2) |SC| liczmy z https://matematykaszkolna.pl/strona/1248.html (x_A−x_s)²−(y_A−y_s)²=|SC| pamiętamy ,ze |SC|=|SA| w miejsce x_A zostaje, a w miejsce y_A wstawiamy równanie prostej AC (y=blabla) i rozwiązujemy (x_A−x_s)²−(y_A−y_s)²=|SC| Napisałem tylko tyle , bo nie mam za bardzo czasu na robienie całego zadania, jak coś nie bedziesz wiedział pytaj. równanie AC mam nadzieje ,ze wiesz jak wyznaczyć

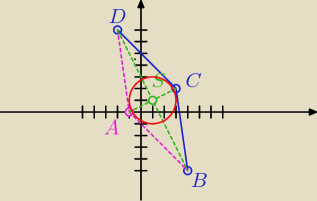
dero2005: obliczamy współczynnik kierunkowy a_BC prostej BC

	yC−yB		2+5		7
aBC =		=		=		= −7
	xC−xB		3−4		−1

obliczamy równanie prostej (boku) DA równoległej do prostej CB i przechodzącej przez punkt D współczynnik kierunkowy a_DA = a_BC = −7 równanie DA y_DA = a_DA(x − x_D) + y_D = −7(x + 2) + 7 = −7x −14 +7 = −7x − 7 y_DA = −7x − 7 obliczamy współczynnik kierunkowy a_CD prostej CD

	yD−yC		7−2		5
aCD =		=		=		= −1
	xD−xC		−2−3		−5

obliczamy równanie prostej (boku) BA równoległej do prostej CD i przechodzącej przez punkt B współczynnik kierunkowy a_BA = a_CD = −1 równanie BA y_BA = a_BA(x − x_B) + y_B = −1(x − 4) − 5 = −x +4 −5 = −x − 1 y_BA = −x − 1 obliczamy współrzędne punktu A (porównujemy równania prostych y_BA i y_DA) −7x − 7 = − x − 1 −7x + x = −1 + 7 −6x = 6 x = −1 y = −7*(−1) −7 = 7 − 7 = 0 A(−1, 0) obliczamy środek odcinka AC (współrzędne punktu S − środek koła wpisanego)

	xA+xC		yA+yC
S=(		;		)
	2		2

	−1+3		0+2
S = (		;		)
	2		2

S= (1 , 1) obliczamy odległość punktu S od prostej np. AD (promień okręgu wpisanego)

	|AxS + ByS + C|
d =
	√A2+B2

równanie ogólne prostej AD 7x + y + 7 = 0

	7*1+1+7		3√2
d =		=
	√72+12		2

równanie okręgu (x−a)² + (y−b)² = r² (x−1)² + y−1)² = ⁹₂