
 cierpliwości, bo dużo pisania.. i rysunek Ci narysuję!
Na bank rpodam rozwiązanie, ale to potrwa
cierpliwości, bo dużo pisania.. i rysunek Ci narysuję!
Na bank rpodam rozwiązanie, ale to potrwa


 Za moment piszę rozwiązanie
Za moment piszę rozwiązanie
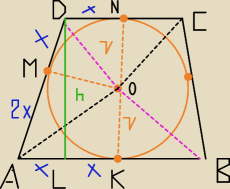
 ΔMOD przystaje do ΔOND kąty OMD = <OND = 90o bo okrąg wpisany
co daje ,że IMDI=INDI = x (wprowadzamy takie oznaczenie
podobnie ΔAKO przystaje do ΔAMO
więc IAKI= IAMI= 2x bo podział ramienia jest w skali 1:2
htrap= 2r = 4
ponieważ trapez jest równoramienny to:IALI =( IABI − IDCI)/2
IDCI = 2x bo N środkiem górnej podstawy i K środkiem dolnej podstawy
zatem IALI= 2x to IABI = 2x
z tw. Pitagorasa obliczamy z ΔALD
x2 +h2 = (3x)2 znając h = 4
wyliczamy "x"
x2 16 = 9x2 => 8x2 = 16 => x = √2
więc już znamy długości dolnej i górnej podstawy:
IABI = 4√2 ICDI = 2√2 h= 4
pole już policz ze wzoru .............
PS: sory, ale chwilowo mnie nie było
ΔMOD przystaje do ΔOND kąty OMD = <OND = 90o bo okrąg wpisany
co daje ,że IMDI=INDI = x (wprowadzamy takie oznaczenie
podobnie ΔAKO przystaje do ΔAMO
więc IAKI= IAMI= 2x bo podział ramienia jest w skali 1:2
htrap= 2r = 4
ponieważ trapez jest równoramienny to:IALI =( IABI − IDCI)/2
IDCI = 2x bo N środkiem górnej podstawy i K środkiem dolnej podstawy
zatem IALI= 2x to IABI = 2x
z tw. Pitagorasa obliczamy z ΔALD
x2 +h2 = (3x)2 znając h = 4
wyliczamy "x"
x2 16 = 9x2 => 8x2 = 16 => x = √2
więc już znamy długości dolnej i górnej podstawy:
IABI = 4√2 ICDI = 2√2 h= 4
pole już policz ze wzoru .............
PS: sory, ale chwilowo mnie nie było podam zaraz drugą część zadania , tzn wskazówki
podam zaraz drugą część zadania , tzn wskazówki
 Może ktoś zna prostszy sposób? ( myślę jednak ,że też taki)
Może ktoś zna prostszy sposób? ( myślę jednak ,że też taki)
| IABI | |
= 2R
| |
| sin<A |
| h | 4 | |||
sin<A = | = > sin<A = | |||
| 3x | 3√2 |
| 2√2 | ||
to sin<A= | ||
| 3 |
| √34 | ||
2R = | ||
| sin<A |
| √34 | ||
R= | ||
| 2√2/3 |
| 3√17 | ||
to R= | ||
| 4 |
 ( masz jakąś odp do tego zadania ?
Pytaj jak czegoś nie rozumiesz?
Idę na herbatkę
( masz jakąś odp do tego zadania ?
Pytaj jak czegoś nie rozumiesz?
Idę na herbatkę  Pozdrawiam
Pozdrawiam
 w obliczeniach brałam dobrze !
w obliczeniach brałam dobrze !


 Rozumiesz "Asiu " to rozwiązanie?
Rozumiesz "Asiu " to rozwiązanie?
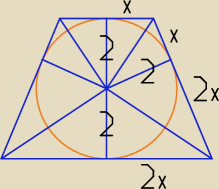 Pole trapezu można wyznaczyć również tak:
x > 0
Wszystkie trójkąty zaznaczone niebieskim kolorem są podobne, stąd mamy proporcję:
2x2 = 2x => x2 = 2 => x = √2
Pole trapezu P = 4*12*2x*2 + 4*12*x*2 = 12x = 12√2
Pole trapezu można wyznaczyć również tak:
x > 0
Wszystkie trójkąty zaznaczone niebieskim kolorem są podobne, stąd mamy proporcję:
2x2 = 2x => x2 = 2 => x = √2
Pole trapezu P = 4*12*2x*2 + 4*12*x*2 = 12x = 12√2
 Pocieszam się tylko tym ,że Basia pisała ,że podobnie rozwiązywała jak ja!
Wysiadam w przedbiegach z Tobą
Pocieszam się tylko tym ,że Basia pisała ,że podobnie rozwiązywała jak ja!
Wysiadam w przedbiegach z Tobą  Miłch snów
Miłch snów
 Podaj " błyskawicą "... R −− okręgu opisanego
Podaj " błyskawicą "... R −− okręgu opisanego
| 3x*4x*√34 | x√34 | √2*34 | 2√17 | √17 | ||||||
R = | = | = | = | = | ||||||
| 4*12x | 4 | 4 | 4 | 2 |
| 3x * 4x * √34 | 3 * √68 | 3*2*√17 | 3√17 | |||||
R = | = | = | = | |||||
| 4 * 8x | 8 | 8 | 4 |

 . Dopiero rano zauważyłem, ze wkleiłem 12x zamiast 8x i szybko poprawiłem.
A wracając do pola tego trapezu. Można go wyznaczyć jeszcze tak:
Pole mniejszego trójkąta P1 = √2.
Skala podobieństwa większego trójkąta do mniejszego jest równa x = √2,
a więc pole większego trójkąta P2 jest 2 razy większe od pola P1 mniejszego trójkąta.
Są 4 mniejsze trójkąty i 4 większe, a więc pole trapezu
P = 4P1 + 4P2 = 4P1 + 8P1 = 12P1 = 12√2
. Dopiero rano zauważyłem, ze wkleiłem 12x zamiast 8x i szybko poprawiłem.
A wracając do pola tego trapezu. Można go wyznaczyć jeszcze tak:
Pole mniejszego trójkąta P1 = √2.
Skala podobieństwa większego trójkąta do mniejszego jest równa x = √2,
a więc pole większego trójkąta P2 jest 2 razy większe od pola P1 mniejszego trójkąta.
Są 4 mniejsze trójkąty i 4 większe, a więc pole trapezu
P = 4P1 + 4P2 = 4P1 + 8P1 = 12P1 = 12√2