twierdzenie cosinusow sonia12: Jeden z kątów trójkąta ma miare (alfa) . stosunek dl. bokow zawartych w ramionach tego trojkata jest rowny 4:1, a srodkowa poprowadzona do dluzszego z nich ma dlugosc s. oblicz dlugosci bokow tego trojkata

Bogdan: Treść jest chyba taka: Jeden z kątów trójkąta ma miare α. Stosunek długości boków zawartych w ramionach tego kąta jest równy 4:1, a środkowa poprowadzona do dłuższego z nich ma długość s. Oblicz długosci boków tego trójkata.

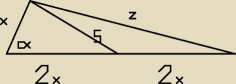
Bogdan: x > 0, z > 0 Dla wyznaczenia długości x korzystamy z wzoru kosinusów: s² = 4x² + x² − 2*2x²cosα => s² = x²(5 − 4cosα)

	s
x =
	√5 − 4cosα

	4s
4x =
	√5 − 4cosα

Długość z też wyznaczamy z wzoru kosinusów: z² = 16x² + x² − 2*4x²cosα => z² = x²(17 − 8cosα)

	s
z = x√17 − 8cosα => z =		* √17 − 8cosα
	√5 − 4cosα

Eta: mnie wychodzi z obliczeń:

	s
ICBI=
	√65− 16cosα

	4s
IACI =
	√65−16cosα

	s(√17 −8cosα
IABI=
	√65− 16cosα

nie usuwając niewymierności oczywiście! Ciekawa jestem jakie Tobie Bogdanie wyszły długości tych boków? może się gdzieś pomyliłam w rachunkach?

Eta: Koszmarne to jest! Tylko nie wiem gdzie sie pomyliłam ,bo wyniki nasze się różnią Nie chce mi się już szukać narazie błędu

Bogdan: Jak wyznaczyłaś Eto 65 − 16cosα ?

Eta: s = IADI −−− tak oznaczyłam s² = IACI² +ICDI² −2IACI*ICDI*cosα IACI= 4ICBI ICDI=¹₂ICBI s² = 16ICBI² +¹₄ICBI² − 4ICBI²*cosα s² = ICBI²( 16 + ¹₄ − 4cosα) s² = ICBI²( ^{65 − 16cosα}₄) s= ICBI*( ^{√65 − 16cosα}₂) więc:

	2s
ICBI =
	√65 − 16cosα

Możesz mi wskazać gdzie popełniam błąd ? bo nie wiem ? .... zgłupiałam !

Eta:

Bogdan: Zwróć Eto uwagę na treść zadania, jest tam informacja, że środkowa s jest poprowadzona do dłuższego z dwóch boków między którymi jest proporcja 1 : 4, między tymi bokami jest kąt α.

Eta: Ok Dzięki! poprostu proporcję nie tą wzięłam oczywiście 1:4 a nie 4:1 zgadza się wynik taki sam jak u Ciebie s² = ICDI² ( 5 − 4cosα) teraz gra i buczy

Bogdan: