 W ostrosłupie prawidłowym trójkątnym krawędź boczna ma długość a , zaś kąt dwuścienny
pomiędzy ścianami bocznymi ma miarę α. Oblicz objętość tego ostrosłupa.
W ostrosłupie prawidłowym trójkątnym krawędź boczna ma długość a , zaś kąt dwuścienny
pomiędzy ścianami bocznymi ma miarę α. Oblicz objętość tego ostrosłupa.
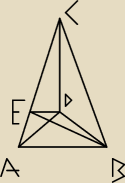 Ozn. jak na rysunku, gdzie BE oraz DE są prostopadłe do AC
Dodatkowo niech
|AC|=|BC|=|DC|=a, b=|AB|=|BD|=|DA|, h=|EB|=|ED|
Wówczas w trójkącie EDB kąt DEB ma miarę α
Stąd i z tw. sinusów wyliczamy, że
b= 2h sin(α/2)
Policzmy jeszcze pole trójkąta ABC na dwa sposoby
pole ABC = ah/2 = b√a2−b2/4
z tych dwóch równań można wyliczyć już b (oraz h), a dalej chyba nietrudno...
Ozn. jak na rysunku, gdzie BE oraz DE są prostopadłe do AC
Dodatkowo niech
|AC|=|BC|=|DC|=a, b=|AB|=|BD|=|DA|, h=|EB|=|ED|
Wówczas w trójkącie EDB kąt DEB ma miarę α
Stąd i z tw. sinusów wyliczamy, że
b= 2h sin(α/2)
Policzmy jeszcze pole trójkąta ABC na dwa sposoby
pole ABC = ah/2 = b√a2−b2/4
z tych dwóch równań można wyliczyć już b (oraz h), a dalej chyba nietrudno...
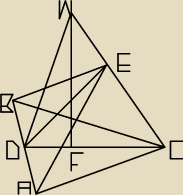 Oznaczenia:
a = |CW| = |AW| = |BW|
b = |AB| = |BC| = |AC|
H = |FW|
w = |DE|
α = |<AEB|
α2 = |<AED|
|<DEC| = 90o
|DC| = 12b√3
|FC| = 13b√3
Oznaczenia:
a = |CW| = |AW| = |BW|
b = |AB| = |BC| = |AC|
H = |FW|
w = |DE|
α = |<AEB|
α2 = |<AED|
|<DEC| = 90o
|DC| = 12b√3
|FC| = 13b√3
| 12b | ||
W trójkącie AED: | = tg(α2) to b = 2wtg(α2)
| |
| w |
| 2aw | 2aw | a | ||||
H = | = | = | ||||
| b√3 | 2w√3tg(α2) | √3tg(α2) |
| a2 | ||
13b2 = a2 − | ||
| 3tg2(α2) |