awl: Proponowałbym uzupełnić ten temat o jednokładność względem dowolnego punktu, nie tylko początku układu współrzędnych.

MuKuL: Zgadzam się w stu procentach z poprzednikiem.

MaTi: Witam. Od 2 lat uczę się do sprawdzianów z matematyki z tej właśnie strony. Podziwiam cię Jakub za to że bezinteresownie pomagasz innym − lepsze to niż wszystkie korepetycje razem wzięte. Zgadzam się z awl i MuKuL, że przydała by się na stronie jednokładność względem dowolnego punktu w układzie współrzędnych. Ale i tak, wielkie THX za stronkę. Pozdrawiam.

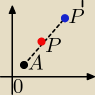
Mateusz: Jednokładnosc względem dowolnego punktu łatwo jest sobie wyprowadzic znając definicje jednokładnosci co widac na powyzszym rysunku A=(a,b),P=(x,y),P'=(x',y') J^k_A(x,y)=(x',y') i stąd {x'=k(x−a)+a {y'=k(y−b)+b

Monic: gratuluję! Genialna strona!

Marcin: Serdecznie dziekuje za wstawienie Niech Ci sie darzy!

Aldo: Dziękuję Mateuszu.

Leo: Mateusz mistrz

paula: Czy na maturze obowiązuje jedynie jednokładność względem punktu (0,0), czy może dowolnego punktu ?!?!

Jakub: Jeśli chodzi o wzory, to wystarczą Ci tylko te względem punktu (0,0).

Enee: Oblicz pole trapezu równoramiennego, którego przekątna p jest prostopadła do ramienia i tworzy z dłuższą podstawą kąt alfa. ..nie wiem jak uzależnić "b" od "p"

ortodo: A jak było z wektorami w jednokładności?