DOROTKA: skąd się dowiedzielismy o tych 2√21 ? NIE ROZUMIEM.

angela: Hej, mam pytanie, czy to zadanie może być rozwiązane w następujący sposób (wtedy zmienia się dziedzina x):

	(x − 2)(x + 2)
h(x) = log2 (x2 − 4) − log2 (x−5) ⇔ log2
	x − 5

zał:

(x − 2)(x + 2)
	> 0 ⇔ (x − 2) (x+2) (x−5) > 0 ⇔ x ∊ (−2,2) u (5, ∞)
x − 5

Jest to błędne?

Jakub: @DOROTKA Te przedziały są zaznaczone na niebiesko, więc to jest link do podstron, gdzie jest napisane skąd to się bierze. @angela

	(x−2)(x+2)
Funkcje h(x) = log2(x2−4) − log2(x−5) i g(x) = log2		nie są takie same i
	x−5

różnią się właśnie dziedziną. Przykładowo policzysz

	(1−2)(1+2)
g(1) = log2		= log233, ale już h(1) nie policzysz, ponieważ po
	1−5)

podstawieniu 1 za x otrzymasz logarytmy z liczb ujemnych w h(x). Tak więc ostrożnie z przekształcaniem funkcji, ponieważ można w ten sposób otrzymać zupełnie inną funkcję, której dziedzina będzie zupełnie inna niż początkowa.

quarhodron: Dlaczego x_w>5 oraz f(5)>0 ? Bardzo proszę o wyjaśnienie. PILNE

quarhodron: oczywiście wiem że x>5 (z dziedziny) ale zakładając x_w>5 przecież pomijamy te ixy na lewo od wierzchołka ?

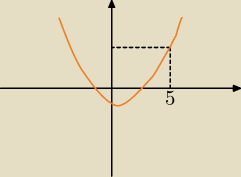
Jakub: Zauważ, że tylko dwa warunki Δ > 0 f(5) > 0 nie wystarczą. Narysowałem parabolę, gdzie te dwa warunki są spełnione, a oba pierwiastki nie są większe od 5. Trzeba dodać trzeci warunek x_w > 5, aby mieć pewność, że parabola jest po prawej stronie liczby 5, przynajmniej jeśli chodzi o pierwiastki. Teraz popatrz na te trzy warunki Δ > 0 f(5) > 0 x_w > 5 Spróbuj narysować parabolę, która spełnia te trzy warunki, a nie ma dwóch pierwiastków lub jeden z nich albo oba są mniejsze od 5. Jak ci się nie uda, to znaczy, że te trzy warunki są wystarczające. Moim zdaniem się ci nie uda

quarhodron: Dziękuje bardzo za wytłumaczenie. Cholernie sprytnie załatwił Pan to zadanie.

quarhodron: Niestety nie udało mi się narysować

orka z worka: Można też zrobić to zadanie wzorami Viete'a. x1>5 i x2>5, czyli x1+x2>10 i (x1−5)(x2−5)>0

Patrycja: Nie zgadzam się z rozwiązaniem. Wchodzę więc w polemikę. Z tego co się pochylilam nad rysunkiem i rozrysowaniem x1, x2, określenie wierzcholka nie gwarantuje rozwiązań większych niż 5. Mniejszy pierwiastek może zostać zlokalizowany przy taki założeniu po lewej stronie liczby 5 mimo, że wierzchołek i drugi pierwiastek znalazłyby się po prawej stronie od 5. Wg mnie rozwiązaniem jest nałożenie warunku >5 nie na wierzchołek a na mniejszy z pierwiastków, czyli

	k − √k2 −20k +16
x1 mniejszy =		> 5, Bo Δ =k2 −20k +16.
	2

Więc ostatecznie mamy 2 warunki 1) Δ> 0 oraz 2) x_{1 mniejszy} > 5 plus dziedzina. Z drugiego wychodzi że k∊R więc ostatecznie zawężenie przedziału k∊ (−∞, 10 − 2√21) ∪ (10 + 2√21, ∞) przez dziedzinę k>0 sprowadza się do calego prawego przedziału k∊ (10 + 2√21, ∞) . Dodatkowo przy takich założeniach niepotrzebne jest zakładanie, że f(5)>0, bo przy zrobionym założeniu na x_{1 mniejszy} biorąc pod uwagę, że współczynnik a>0, parabola ma widełki do góry jakby z urzędu, tak po prostu . Uprzejmie proszę o konfrontację mojego toku myślenia i ewentualną weryfikację