Justyna: wszystko jest dobrze wytłumaczone ale mi brakuje tutaj różnicy symetrycznej, której nie bardzo rozumiem. dobrze by było gdybyście zamieścili również i to. pozdrawiam.

janinka: ale czemu przy roznicach itd przedzila z koleczkiem niepokolorowanym staje sie nagle zamkniety > zamiast )

Jakub: Różnica A\B to wszystkie liczby, które należą do przedziału A, ale NIE NALEŻĄ do przedziału B. Tak więc jeżeli w przedziale A jest liczba 2 (nawias ostry, kółko zamalowane) i w przedziale B też jest liczba 2, to w A\B tej liczby 2 już nie ma (nawias okrągły, kółko otwarte).

Mateo: Bardzo fajnie wytłumaczone i objaśnione! Wszystko wyraźne i przejrzyste! Jutro kartkówka więc na pewno dużo mi ta stronka pomogła.Pozdrawiam

Daniello : W przykładzie czwartym, suma A i B, można B zapisać jako podzbiór zbioru A

adrianpotrzebujepomocy: nie kapuje wstawiania odpowiednich nawiasów w A\B i B\A wiem tylko że w A\B pierwszy nawias sie nie mienia ac z pozostałymi ?

Marta: Czy w pierwszym przykładzie w B' nie powinien być inny nawias przy 4?

Jakub: Jest dobrze. Przedział B=(1,4> zawiera liczbę 4, czyli dopełnienie B już jej nie zawiera, dlatego przy 4 jest okrągły nawias.

Kasiurda: zauwazyłam ze jesli zbiory sie pokrywają to te punkty wspolne wysraczy jedynie zamienić na przeciwne tak wiec tuu cały kłopot !

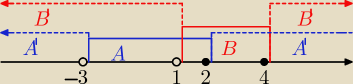
Gustlik: Lepiej rysować sposobem jak powyżej − metoda mieszana: szkolna + metoda Bogdana. Przedział otwarty − kropka pusta i poza przedziałem, przedział domknięty − kropka zamalowana i w przedziale. Zamalowywanie kropek ma na celu jedynie zmylenie nauczycieli, żeby się nie przyczepiali do uczniów, bo Bogdan robi bez zamalowywania, ale wtedy to się nauczycielom rzuca w oczy i mają oni "wąty" do uczniów za to. Tu wyjaśniłem tę metodę : https://matematykaszkolna.pl/forum/forum.py?komentarzdo=i3 . A=(−3, 2> B=(1, 4> AUB=(−3, 4> A∩B=(1, 2> A\B=(−3, 1> (1 zostanie w przedziale, nieważne że nie jest zamalowana, widać to z rysunku) B\A=(2, 4> (2 nie zostanie w przedziale, nieważne że jest zamalowana, widać to z rysunku) A'=(−∞, −3>U(2, +∞) B'=(−∞, 1>U(4, +∞)

KalAmburka: Skąd wiadomo kiedy przy A' lub B' dać który nawias? Np. A=(2, 6>, a A'=(−∞, 2>U(6, +∞)

Jakub: Nawiasy okrągłe (, ) oznaczają, że liczby stojące przy nich nie należą do przedziału. Nawiasy ostre <, > oznaczają, że liczby stojące przy nich należą do przedziału. Jak masz A = (2, 6>, to 2 nie należy do przedziału A, a 6 należy. A' oznacza dopełnienie przedziału A. W dopełnieniu zawierają się wszystkie liczby, które nie należą do A. Tak więc w dopełnieniu A znajdzie się 2, ale 6 już nie. Z tego powodu przy 2 jest ostry nawias, a przy 6 już nie.

adam: a dlaczego w przykładzie A=(−3,2> B=(1,4> w pod podpunkcie b/a ( do b należy i do a nie należy) jest <2,4> a nie <4,2> prosze o odpowiedź...