Monia: Dlaczego funkcja nie przechodzi przez punkt 0 ?

Jakub: Która funkcja?

Jakub: Jeżeli funkcja liniowa nie jest funkcją stałą, to dziedziną i zbiorem wartości są wszystkie liczby rzeczywiste. np. y=2x+5 D=R, ZW=R y=−3x D=R, ZW=R y=6 D=R, ZW={3} y=−4 D=R, ZW={−4}

magdzik: nie ma tu wzoru na miejsce zerowe funkcji wygląda on tak; −^b_a

Jakub: Miejsce zerowe każdej funkcji, nie tylko liniowej, to taki x, dla którego y=0 Dla funkcji liniowej y = ax+b 0 = ax+b −b = ax /:a −^b_a = x x = −^b_a Przykład: Dla funkcji y=3x−2 0 = 3x−2 −3x = −2 /:(−3) x = ⁻²₋₃ = ²₃ Wzoru, który napisałaś, nie ma w karcie wzorów rozdawanych na maturze. Dlatego lepiej pamiętać SPOSÓB liczenia miejsca zerowego, a nie WZÓR. W dodatku ten sposób działa też dla innych funkcji nie tylko liniowych.

1985Gonzo: Witam. Sam uczę się w szkole wieczorowej i pomagam reszcie klasy z opanowaniem materiału. Ta strona jest w tym bardzo pomocna, ale brakuje tutaj postaci ogólnej prostej w układzie współrzędnych. Mógłbyś to tutaj Jakub gdzieś dorzucić Z jakimś prostym opisem przekształcenia do postaci kierunkowej i odwrotnie

Jakub: Równanie ogólne prostej z przykładami jest w dziale geometria analityczna.

Dejziii: ja i tak tego nie umiem

martyna159: ta strona jest rewelacjna

dominika: wzor na miejsce zerowe jest w tablicy wzorow do matury

Jakub: Jesteś pewna? Na której stronie? http://www.cke.edu.pl/images/stories/09_MATURA_proba_mat/tablice.pdf

fredzel: skad sie odczytuje "a" na wykresie?

Mała. <3: Wow, już teraz to zrozumiałam! Ekstra stronka !

karolina: a ja jestem taka tępa z matmy, ze i tak nic nie rozumiem, ale przyznam, ze strona świetna

szympans: strona jest extra

Azallia : Wyznacz punkty przecięcia wykresu funkcji f z osiami układu współrzędnych i naszkicuj ten wykres. Określ monotoniczność tej funkcji f(x)=1/3 x+2. blagam pomocy! ciągi liniowe to dla mnie magia..

moni30003: Nie wie skąd jest wyznaczone a.

Dan: Strona jest rewelacyjna a wszystko jest tutaj tak dokładnie opisane że spokojnie można odstawić korepetycje i uczyć się ze stronki bez niczyjej pomocy.

neti: skad wiemy jaką wartość przyjmuje a?

Jakub: "a" to liczba, która stoi przed "x" np. dla y = 3x+2 mam a = 3 dla y = −7x+5 mam a = −7

Patryk: Jaki zbiór wartości ma funkcja liniowa y=2x+3 ? zw=D

Jakub: Zbiór wartości to zbiór wszystkich liczb rzeczywistych. ZW=R.

karina: otoz to skad wiemy ze a=2 . wszystko rozumiem tylko nie to

Jakub: Funkcja liniowa ma wzór y=ax+b. Jak widać, litera "a" stoi przy x. Dla funkcji y=2x+3 przy x stoi 2 i dlatego a=2.

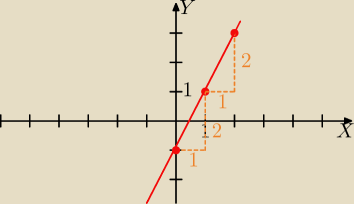
Gustlik: Geometryczny sposób rysowania wykresu funkcji liniowej − można narysować prostą bez tabelki. 1. Zaznaczam wyraz wolny b na osi OY − mam pierwszy punkt − prosta y=ax+b przecina oś OY w pkt. (0, b). 2. Gdy a jest całkowite − od tego punktu "jadę" o 1 w prawo i o |a| w górę, gdy a>o lub o 1 w prawo i o |a| w dół, gdy a<0, rysuję w ten sposób "schodki" i otrzymuję kolejne punkty prostej. Np. dla y=2x−1 wykres wygląda tak jak na rysunku.

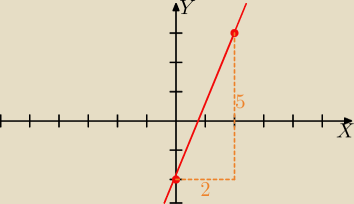
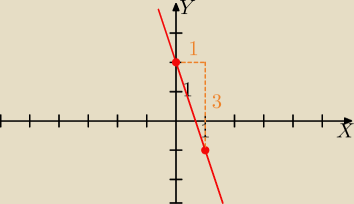
Gustlik: Teraz narysuję wykres funkcji y=−3x+2 − wykres przechodzi przez pkt. (0, 2) na osi OY potem o 1 w prawo i o 3 w dół, bo a=−3..

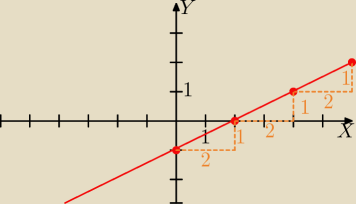
Gustlik: Gdy współczynnik kierunkowy jest ułamkiem zwykłym, to zaznaczam (0, b) na osi OY, a potem "jade" o mianownik w prawo i o licznik w pionie (w górę gdy a>0 lub w dół, gdy a<0), czyli mianownik to "szerokość schodka", a licznik − "wysokość schodka".

	1
Na rysunku wykres funkcji y=		x−1 .
	2

Gustlik:

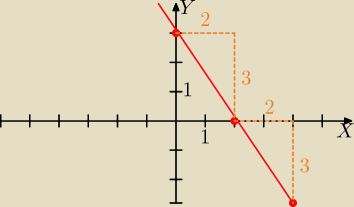
	3
Teraz narysuję wykres y=−		x+3. "Schodki" idą o 2 w prawo (mianownik) i o 3 (licznik) w
	2

dół, bo a jest ujemne.

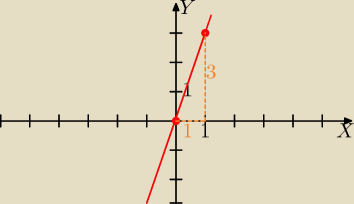
Gustlik: Wykres funkcji y=ax (gdy b=0), np. y=3x − wtedy "startujemy" z początku układu współrzędnych, bo prosta przechodzi przez pkt (0, 0). Na rysunku wykres funkcji y=3x.

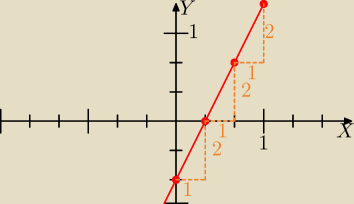
Gustlik: Gdy wyraz b jest ułamkiem − zmieniam skalę na obu osiach tak, że mianownik tego ułamka przedstawia liczbę działek (np. kratek) na jednostkę. Wtedy punkt (0, b) bedzie na punkcie kratowym. Zmiana skali nie ma wpływu na współczynnik kierunkowy, a więc na konstrukcję "schodków".

	2		1
Na rysunku wykres funkcji y=2x−		− czyli 3 kratki na jednostkę (jedna kratka to		).
	3		3

Zmiana skali nie ma wpływu na współczynnik kierunkowy − "schodki" rysujemy jadąc o 1 kratkę w prawo i o 2 kratki w górę (na rysunku liczby 1 i 2 zaznaczone na brązowo oznaczają

	1
liczbe kratek − dla uproszczenia konstrukcji − , a nie jednostek, faktycznie jest to o
	3

	2
w prawo i o		w górę).
	3

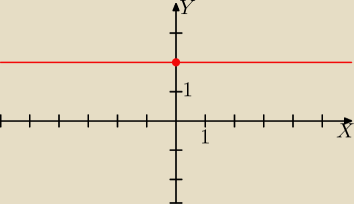
Gustlik: Dla funkcji stałej y=b (a=0) zaznaczam punkt (0, b) na osi OY i rysuję "poziomą" prostą równoległą do osi OX przechodzącą przez ten punkt. Na rysunku wykres funkcji y=2.

Gustlik:

	1
Gdy funkcja jest dana wzorem, np. y=2		x−2, zamieniam liczbe mieszaną na ułamek
	2

	5
niewłaściwy, wzór wtedy przyjmie postać y=		x−2 i rysuję "schodki" w zasad dla
	2

współczynników ułamkowych.

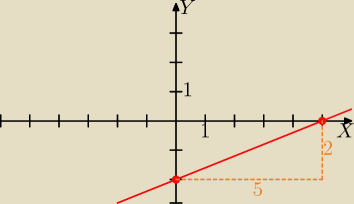
Gustlik: Gdy występują ułamki dziesiętne, zamieniam je na zwykłe, potem skracam (o ile się da) i rysuję wykres jak dla współczynników ułamkowych. Np. y=0,4x−2

	4		2
0,4=		=
	10		5

Wzór będzie wyglądał tak:

	2
y=		x−2.
	5

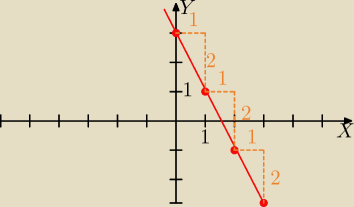
Gustlik: Gdy prosta jest dana równaniem ogólnym Ax+By+C=0 − przekształcam je na kierunkowe i rysuję jak wykres funkcji liniowej. Np. 2x+y−3=0 y=−2x+3

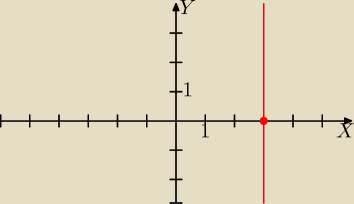
Gustlik: Dla prostej "pionowej" x=c zaznaczam punkt (c, 0) na osi OX i rysuję "pionową" prostą równoległą do osi OY przechodzącą przez ten punkt. UWAGA ! TAKA PROSTA NIE JEST WYKRESEM FUNKCJI ! Na rysunku prosta x=3.

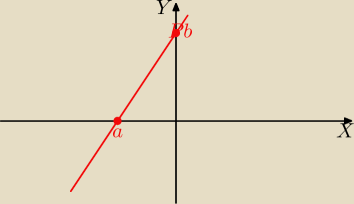
Gustlik: Warto jeszcze zwrócić uwagę na jeszcze jedną postać równania prostej − równanie odcinkowe. Prosta dana takim równaniem jest niezwykle łatwa do narysowania, łatwiejsza nawet od funkcji liniowej, a tym bardziej od równania ogólnego. To równanie ma postać:

x		y
	+		=1
a		b

Zaznaczamy więc na osi OX punkt (a, 0) oraz na osi OY punkt (0, b) i przez te punkty prowadzimy prostą.

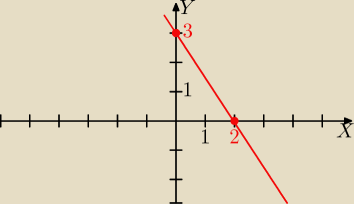
Gustlik: Przykład prostej danej równaniem odcinkowym:

x		y
	+		=1
2		3

madzik: Witam a co myslicie o funkcji liniowej? na tablicach matematycznych nie ma kompletnie zadnych wzorow do niej a jest w zakresie, myslicie ze tych wzorow trzeba sie na blache wykuc

Gustlik: Są wzory w dziale "Geometria analityczna", choc rzeczywiście mogłoby być tych wzorów więcej.

Patrycja: Podaj współrzędne punktów przecięcia wykresu funkcji z osią Oy i Ox a) f (x)=x+6

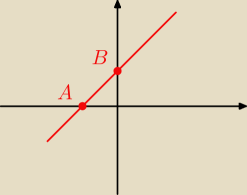
annmaria: Punkt A to miejsce zerowe funkcji, należy przyrównać wzór funkcji do 0 czyli 0=x+6 x=−6 A=(−6,0) Natomiast punkt B to odczytujemy z równania kierunkowego funkcji f(x)=ax+b, dla danej funkcji: f(x)=x+6 b=6 B=(0,6)

Dociekliwy: Albo jestem ślepy albo jest podany "wzór" na współrzędne punktu przecięcia z osią OY, a nie ma podobnego dla OX. Jak prosto wywnioskować: punkt przecięcia z OX jest wtedy kiedy y = 0. Więc podstawiając do

	b
wzoru y = ax + b wychodzi: x = −
	a

	b
Więc, punkt przecięcia funkcji liniowej z osią X to: (−		, 0).
	a

Am I right?

Jakub: Dokładnie tak. Właśnie wyprowadziłeś wzór na współrzędne punktu przecięcia wykresu funkcji liniowej z osią OX.

Kass: A jeżeli mamy taką funkcję: y=− x + 4 to współczynnik kierunkowy wynosi −1 czy 0? Kiedy on wynosi zero?

Kamyka: Kass współczynnik kierunkowy wyniesie zero kiedy nie będzie żadnego x bo: 0 pomnożone przez x = 0. Czyli nie będzie nic. Jeśli odpowiesz sobie przez jaką liczbę należy pomnożyć x, żeby wyszło −x to znajdziesz współczynnik kierunkowy stojący przy x.

Leszek: Postać kierunkowa ma jedną bardzo dużą wadę. Nie można w tej postaci podać prostej równoległej do osi OY dlatego wolę zdecydowanie postać ogólną Ax+By+C=0 a jeszcze lepiej gdy A²+B²=1 wtedy A=cos (alpha) B=sin (alpha) a C=−rho gdzie alpha to kąt nachylenia prostej do osi OY a rho to odległość prostej od punktu (0,0). Oczywiście alpha i rho to litery greckie

Jakub: A = cosα, B = sinα, C = ϱ

Gustlik: Leszku, prosta równoległa do OY ma równanie x=c (prosta "pionowa"), gdzie c to współrzędna, w której ta prosta przecina oś OX. Zatem równoległe bedą dwie proste tego typu, np. x=−3 i x=1, czyli muszą to być dwie proste "pionowe". Ja osobiście wolę postać kierunkową, bo wtedy traktuję to jak zwyk łą funkcję liniową, która jest o wiele łatwiejsza w rozwiązywaniu zadań i lepiej przyswajalna przez uczniów, z kierunkowej można łatwo narysować wykres "schodkami" jak opisałem powyżej, można łatwiej wyznaczyć prostą równoległą czy prostopadłą do danej itp. Większość uczniów też woli postać kierunkową, a jak maja w zadaniu ogólną to przekształcają do kierunkowej i na kierunkowej liczą.

szczęściara : Dzięki Panu zdałam dzisiaj komisa z matematyki na 4 !

Julia: przygotowuję się już długo do olimpiad, ale, niestety dopiero kilka dni temu znalazłam tą stronę i jest cudowna! wszystko opisane w prostym języku, tablice matematyczne gdzie trzeba jedno zdanie czytać kilka razy, żeby dopiero przetrawić, mogą się kłaniać, tłumaczenia są podobne, do sposobów mojego nauczyciela, a mogę czytać je sobie w domu, wielkie dziękuje

orka z worka: Pomoże ktoś z zadaniem? Miejscem zerowym funkcji f(x)=ax+b jest wartość liczbowa wyrażenia (2−√√x)(2+√√x) dla x=9. (Oczywiście √√x to pierwiastek 4 stopnia z x, ale nie wiedziałam jak to inaczej zapisać) a) Wyznacz a Wydaje mi się, że w zadaniu jest za mało informacji, żeby wyznaczyć a. Jak podstawię 9 za x do tego równania wyżej, to wyjdzie mi 1. Czyli miejscem zerowym jest 1. Wtedy mam równanie a*1+b=0, ale mam dwie niewiadome w jednym równaniu, więc nie mogę obliczyć a. Mogę tylko napisać, że a=−b b) Dla jakich argumentów x funkcja f przyjmuje wartości większe od 1/3? ax+b>1/3 za a podstawiam −b −bx>1/3−b dzielę obie strony przez −b dla b<0 (czyli −b>0) otrzymuję rozwiązanie x>−1/3b+1 a dla b>0 x<−1/3b+1 I tutaj pojawia się moje pytanie. Czy da się rozwiązać to zadanie tak, aby wyliczyć wartość liczbową a i konkretny przedział w podpunkcie b, czy muszę to zostawić tak jak jest?

orka z worka: ok, już wiem jak zapisać pierwiastek 4 stopnia. Byłam zbyt leniwa, żeby kliknąć w przycisk pod przykładami, sorki

Jakub: Zgadza się. Jak masz jeden punkt (dwie współrzędne x i y), to nie wyznaczysz prostej f(x)=ax+b, bo przez jeden punkt przechodzi ich nieskończenie wiele. Potrzebujesz jeszcze jakiś danych o funkcji f.